Perimeter And Area Of Plane Figures Explained

A question may arise in your mind when you see a plane “what is a plane figure”? A plane shape is a closed, two-dimensional, or flat figure. The characteristics of various plane shapes vary, such as the number of sides or corners (or vertices). We will require several parameters to determine a figure's area depending on its form.

Two plane figures must have the same shape and size in order to have the same area. You are also going to learn about the perimeter of plane figures and formulas for rectangles.

Perimeter of a Plane Figure

The entire distance surrounding a plane figure's boundaries is known as the perimeter of plane figures. The lengths of each side of the figure are added to determine the perimeter. We measure the perimeter using one-dimensional units like metres or centimetres since it is a length.

Due to the nature of the perimeter, it is possible for two figures that have different shapes to have the same perimeter depending on the dimensions of their sides. For example, it is possible to form a circle using a string and then use the same string to form a square. Depending on the figure's shape and the number of sides, the perimeter formula varies for various plane shapes.

Area of a Plane Figure

The region that a plane figure covers is referred to as the area of the plane figure. Area is a two-dimensional measurement, so we use square units like $\mathrm{m}^{2}$ or $\mathrm{cm}^{2}$ to measure it. The plane figure's shape affects the area formula.

Formulas for a Rectangle

A rectangle is defined as a four-sided $2 D$ figure with right angles. All interior angles in a rectangle measure $90^{\circ}$ and their opposite sides are parallel and equal.

A Rectangle

Area Formula $=a \times b$

Perimeter Formula $=2(a+b)$

where $a$ represents the width of the rectangle and $b$ represents its base.

Formulas of Area and Perimeter for a Square

A square is a figure in two dimensions with four equal sides. Since all of a square's inner angles are 90 degrees, it is a particular kind of rectangle.

A square

Area Formula $=l^{2}$

Perimeter Formula $=4l$

where $I$ stands for one of the square's sides' length.

Formulas of Area and Perimeter for a Triangle

The triangle is a 2D figure with three sides. The equilateral triangle, the isosceles triangle, and the scalene triangle are the three different forms of triangles based on the lengths of their sides. The formulas for calculating area and perimeter are the same for any type of triangle.

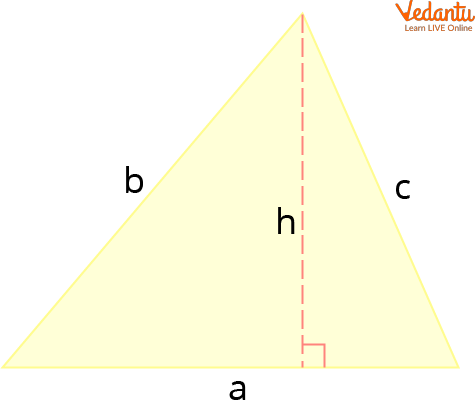
A Triangle

Area Formula $=\dfrac{1}{2} h a$

Perimeter Formula $=a+b+c$

where $a, b, c$ represent the lengths of the sides of the triangle, $h$ represents the height, and a represents the base of the triangle.

Formulas of Circumference and Area for a Circle

A fully round shape is what defines the circle as a 2D figure. The area and perimeter of a circle are determined by its radius.

A circle

Area Formula $=\pi r^{2}$

Perimeter Formula $=2 \pi r$

where $r$ represents the radius of the circle and $\pi$ is a mathematical constant that has a value of $3.1415 \ldots . .$

Now let us discuss some area of plane figures questions and answers.

Solved Examples

The following exercises are resolved using the area and perimeter formulae of various planar figures. There is a solution for each exercise where you can see the steps taken.

Example: 1 What is the area of ​​a triangle that has a base of 9m and a height of 8m?

Ans: We know that the area of ​​any triangle can be found by multiplying its base and height and dividing by two. So, we have:

$A=\dfrac{1}{2} b h$

$A=\dfrac{1}{2}(9)(8)$

$A=36$

So, the area of the triangle is $36 \mathrm{~m}^{2}$.

Example: 2 What is the area and perimeter of a square with sides that are 11m long?

Ans: By squaring the length of one of the sides, we can get the area. The perimeter is calculated by multiplying one of the side's length by four. So, we have:

Area of square$=l^{2}$

$A=(11)^{2}$

$A=121 \mathrm{~m}^{2}

Perimeter of square

$p=4l$

$p=4(11)$

$p=44 m$

So, the area of the square is $121 \mathrm{~m}^{2}$ and the perimeter is $44 \mathrm{~m}$.

Example: 3 A rectangle has sides of length 12m and 15m. What is its perimeter?

Ans: By summing the side lengths and multiplying by two, we can get the rectangle's perimeter:

$p=2(a+b)$

$p=2(12+15)$

$p=2(27)$

$p=54 m$

Practice Questions

1. A circle with a radius of 8m has what area and perimeter?

Ans: The circle's area is $201.1 \mathrm{~m}^{2}$, and its circumference is 50.3m.

2: What is the area of ​​a triangle that has a height of 12m and a base of 11m?

Ans: $66 \mathrm{~m}^{2}$

Summary

The perimeter or boundary of an object is referred to as an object's form. A two-dimensional closed figure with no thickness is referred to as a plane shape. In geometry, a plane is a level surface that goes on forever in all directions. The region that an object's shape defines as its area. The plane area of a figure or any other two-dimensional geometric shape in a plane is how much space it occupies. All forms' areas vary depending on their dimensions and characteristics. There are several shapes with various areas. A kite's area is not the same as the size of the square.

The whole distance around a shape is referred to as its perimeter. In essence, the length of any shape when it is expanded in a linear form equals its perimeter. A shape's perimeter in a two-dimensional plane is its complete circumference. Depending on their measurements, distinct shapes' perimeters may be equal in length.