Nonagon: How is it in Shape?

Does Geometry interest you? Then do you know how many sides a nonagon has? A nonagon is a kind of polygon that consists of nine sides and nine angles. The term ‘nonagon’ has been derived from the Latin word ‘nonus’, which means nine, and the Greek word ‘gon’, which means sides. It also has another name, ‘enneagon’, that is derived from the Greek word ‘enneagonon’, translating to nine corners. Despite ‘enneagon’ being a more appropriate term for this shape, ‘nonagon’ is more often used owing to the simplicity of the name and its convenience in use. 

Regular Nonagon

Different Types of Nonagon

Based on their sides, angles, and vertices, nonagons can be categorised as follows: 

• ccc: A regular nonagon has nine sides of equal length and nine interior angles, each of which measures 140⁰, and has exterior angles measuring 40⁰ each. It has nine lines of symmetry and rotational equilibrium of order nine. All regular nonagons are convex.

• Irregular Nonagon: An irregular nonagon does not have all sides or all interior angles equal. However, the sum of all the nine interior angles measures up to 1260⁰. Irregular nonagons can be both convex and concave.

• Convex Nonagon: A convex nonagon has all nine vertices pointing outwards. All interior angles of this type of nonagon measure less than or equal to 180⁰ and all diagonals are bounded by the closed figure. Convex nonagons can be both regular and irregular.

• Concave Nonagon: A concave nonagon has at least one vertex pointing inwards, having an interior angle that is greater than 180⁰. It has at least one diagonal lying outside the closed figure. Therefore, all concave nonagons are irregular.

Properties of a Regular Nonagon

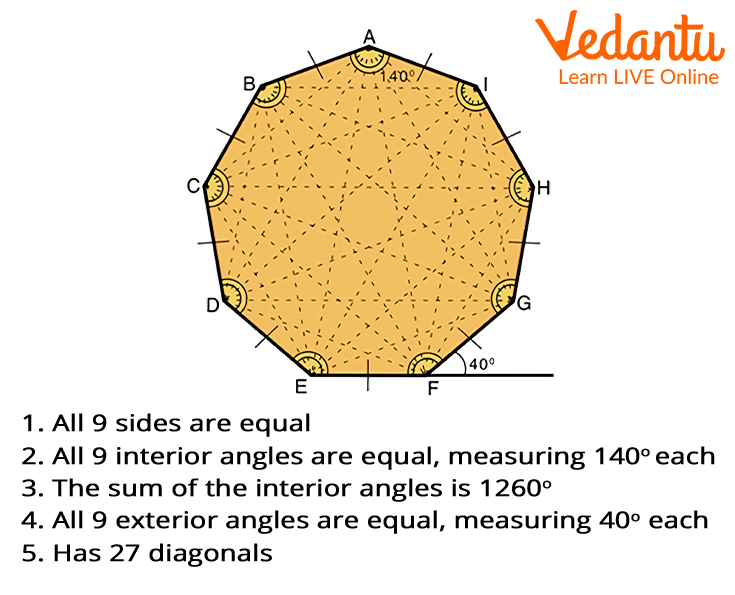
• All 9 sides are of equal length. For instance, in a nonagon ABCDEFGHI, AB = BC = CD = DE = EF = FG = GH = HI = IA.

• It comprises 9 interior angles, each measuring 140⁰. Hence, ∠ABC = ∠BCD = ∠CDE = ∠DEF = ∠EFG =∠FGH = ∠GHI = ∠HIA = ∠IAB.

• All 9 interior angles add up to 1260°. Therefore, ∠ABC + ∠BCD + ∠CDE + ∠DEF + ∠EFG + ∠FGH + ∠GHI + ∠HIA + ∠IAB = 1260⁰.

• It consists of 9 exterior angles, each measuring 40⁰.

• It has 27 diagonals, that is, AC, BD, CE, DF, EG, FH, and GI.

Properties of a Regular Nonagon

Note: Even in an irregular nonagon, the sum of the interior angles will be 1260⁰.

Some Formulas Related to a Regular Nonagon

Perimeter

The formula for the perimeter (P) of a regular nonagon ABCDEFGHI 

 P = 9a,

where a = length of each side of the nonagon, since all 9 sides are equal in a regular nonagon,  that is, a = AB = BC = CD = DE = EF = FG = GH = HI = IA.

Sample Problem: Determine the perimeter of a regular nonagon, each of whose sides measures 9 cm.

Solution: It is given that a = 9 cm.

Since Perimeter (P) = 9a,

Then, the required perimeter P = 9 x 9 cm

                                                      = 81 cm

Area

The formula for determining the area of a regular nonagon ABCDEFGHI is as follows:

Area (A) = \[ \frac{9}{9} \] (a²cot \[ \frsc{π}{9} \] ), 

where a = side length = AB = BC = CD = DE = EF = FG = GH = HI = IA, and π = 180⁰.  

Angles

There are three major angle formulas concerned with regular nonagons - sum of interior angles, individual interior angles, and exterior angles. They can be elaborated as follows:

• Sum of Interior Angles - It is the sum of the measures of all the interior angles taken together in a nonagon. The formula for the sum of interior angles in a regular nonagon is given below:

Sum of the interior angles = (n-2) x 180⁰, where n = number of sides 

In nonagon ABCDEFGHI, n = 9

Therefore,

Sum of the interior angles = (9 -2) x 180⁰

= 1260⁰

• Individual Interior Angle - The measure of an individual interior angle in a regular nonagon can be obtained by dividing the sum of all the interior angles by the number of sides in the nonagon. The formula to obtain the value of an individual interior angle of a regular nonagon is given below:

One interior angle = (n-2) x 180⁰/n, where n = number of sides 

In nonagon ABCDEFGHI, n = 9

Hence,

Sum of the interior angles = (9-2) x 180⁰/9

= 140⁰

• Exterior Angle - An exterior angle is an angle formed by any side of a nonagon and the extension of its adjacent side. The formula to find the value of an exterior angle is given below:

Exterior angle = 360⁰/n, where n = number of sides

In nonagon ABCDEFGHI, n = 9

Therefore,

Exterior angle = 360⁰/9

= 40⁰

Nonagons may not be as commonly observed as other shapes, like circles, squares, and triangles, but their application in art and architecture is no less crucial. The following image is that of the US Steel Building, Pittsburgh, Pennsylvania. Although it may look like a triangular structure at a glance, taking a closer look will reveal its nonagonal aspects, that is, the 6 extra line segments ingrained in the magnificent architecture.

US Steel Building, Pittsburgh, Pennsylvania

Conclusion

To summarise the concept of nonagon, it is a two-dimensional figure (polygon) with nine sides and nine angles. It has 4 major types - regular, irregular, convex, and concave. Most of the properties and formulas are only applicable to regular nonagons, which have equal sides, and their interior and exterior angles are also equal, each measuring 140⁰ and 40⁰, respectively. However, all nonagons have a total interior angle sum of 1260⁰.