Multiple and Submultiple Angles Formula: Concepts, Examples & Uses

Multiple and submultiple angles formula is a mathematics formula that provides the trigonometry ratios for determining various angles of the triangle. These types of formulas are important because they help provide information about the shape, size and location of a given triangle. In trigonometry, the three branches of trigonometry are named after the types of angles they measure: sine, cosine, and tangent. This article will provide you with information on how to work out the two or more different angles in a triangle using multiple and submultiple angles formula.

Meaning of Multiple and Sub Multiple Angles

Let A be any angle . For this angle A , the multiple angles will be 2A , 3A , 4A and so on. To make it more easy to understand, we can assume that what the answer will be if we multiply 2 in A, which is our angle. The answer will be 2A. Again if we multiply 3 with A, the answer will be 3A. Again if we multiply 4 with A, the answer will be 4A . In the same way we can find multiple angles of any given angle.

As we have clearly discussed, the multiple angles of any given angle . Now let us discuss what the sub multiple angles are.

Let there be an angle A, the sub multiple angles for this will be $\dfrac{A}{2}$, $\dfrac{A}{3}$, $\dfrac{A}{4}$ and so on.

For better understanding we will take a simple example . What will be the answer if we multiply $\dfrac{1}{2}$ with A, which is a given angle. The answer will be $\dfrac{A}{2}$. In the same way if we multiply $\dfrac{1}{3}$ with A, the answer will be $\dfrac{A}{3}$. And so on.

For better understanding, find the multiple angles of given angles:

Q 1. What will be the sub multiple angle of X ?

(A) $\dfrac{X}{2}$

(B) $\dfrac{D}{2}$

(C) 2X

(D) $\dfrac{D}{2}$

Ans: $\dfrac{X}{2}$

Q 2. What will be the sub multiple angle of D ?

(A) $\dfrac{X}{2}$

(B) $\dfrac{D}{2}$

(C) 2X

(D) $\dfrac{G}{2}$

Ans: $\dfrac{D}{2}$

Explanation of Quadrants

When axis X and Y intersect each other at 90 degrees, we get four regions. These regions are called quadrants.

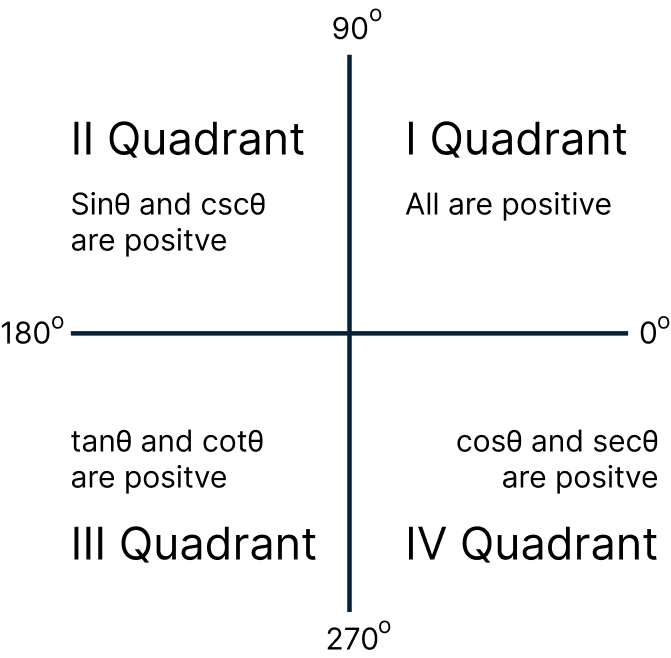
Quadrants

As shown above in figure, there are four regions. The upper right part is called the first quadrant, and it is the positive region. The upper left region is called the second quadrant, and it has minus and positive signs. The lower left region is called the third quadrant, and it has a minus sign, and the lower right region is called the fourth quadrant, and it has positive and negative signs.

Trigonometric Ratios

In a right angle triangle, the base of the triangle is called “base”. In the figure below, OA is the base. The standing straight line of the triangle is called the perpendicular of the triangle. In the below figure AB is the perpendicular of the triangle.This AB and OA make 90 ° angle. And OB is the hypotenuse of the triangle.

Right angled triangle

$\sin \theta=\dfrac{\text { opposite }}{\text { hypotenuse }}=\dfrac{A B}{O B}$

$\cos \theta=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{O A}{O B}$

$\tan \theta=\dfrac{\text { opposite }}{\text { adjacent }}=\dfrac{A B}{O A}$

$\operatorname{cosec} \theta=\dfrac{1}{\sin \theta}=\dfrac{O B}{A B}$

$\sec \theta=\dfrac{1}{\cos \theta}=\dfrac{O B}{O A}$

$\cot \theta=\dfrac{1}{\tan \theta}=\dfrac{O A}{A B}$

Trigonometry Table

As shown in the figure below, you can see the table. It is called a Trigonometry table. We can also call it a table of angles. The value of sin 0 will be 0. The value of sin 30 will be $\dfrac{1}{2}$. The value of cos 0 will be 1. The value of tan 0 will be 0, the value of cot 0 will be infinity. The value of sec 0 will be 1. The value of cosec 0 will be infinity. In the same way you can read this table.

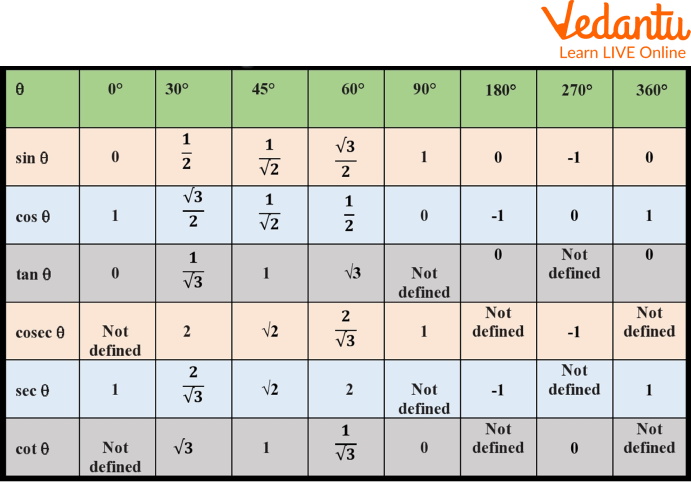
Table of Angle

Trigonometry Ratios Formulas Based on Multiple and Submultiple Angles

There are some basic formulas given below for multiple angles.

• $\sin (A \pm B)=\sin A \cos B \pm \cos A \sin B$

• $\cos (A \pm B)=\cos A \cos B \pm \sin A \sin B$

• $\tan (A \pm B)=\dfrac{\tan A \pm \tan B}{1 \pm \tan A \tan B}$

• $\sin 2 A=2 \sin A \cos A=\dfrac{2 \tan A}{1+\tan ^2 A}$

• $\cos 2 A=\cos ^2 A-\sin ^2 A=\dfrac{1-\tan ^2 A}{1+\tan ^2 A}=2 \cos ^2 A-1=1-2 \sin ^2 A$

• $\sin 3 A=3 \sin A-4 \sin ^3 A$

• $\cos 3 A=4 \cos ^3 A-3 \cos A$

• $\tan 3 A=\dfrac{3 \tan A-\tan ^3 A}{\dfrac{1-3 \tan ^2 A}{A}}$

• $\sin \dfrac{A}{2}=\sqrt{\dfrac{1-\cos A}{2}}$

• $\cos \dfrac{A}{2}=\sqrt{\dfrac{1+\cos A}{2}}$

• $\tan \dfrac{A}{2}=\sqrt{\dfrac{1-\cos A}{1+\cos A}}=\dfrac{1-\cos A}{\sin A}=\dfrac{\sin A}{1+\cos A}$

• $\sin C+\sin D=2 \sin \dfrac{C+D}{2} \cos \dfrac{C-D}{2}$

• $\sin C-\sin D=2 \cos \dfrac{C+D}{2} \sin \dfrac{C-D}{2}$

• $\cos C+\cos D=2 \cos \dfrac{C+D}{2} \cos \dfrac{C-D}{2}$

• $\cos C-\cos D=2 \sin \dfrac{C+D}{2} \sin \dfrac{D-C}{2}$

• $\tan C+\tan D=\dfrac{\sin (C+D)}{\cos C \cos D}$

• $\sin (A+B) \sin (A-B)=\sin ^2 A-\sin ^2 B$

• $\cos (A+B) \cos (A-B)=\cos ^2 A-\sin ^2 B$

• $\sin ^2 A=\dfrac{1}{2}(1-\cos 2 A)$

• $ \cos ^2 A=\dfrac{1}{2}(1+\cos 2 A)$

• $\tan ^2 A=\dfrac{1-\cos 2 A}{1+\cos 2 A}$

• $\sin ^3 A=\dfrac{3 \sin A-\sin 3 A}{4}$

• $\cos ^3 A=\dfrac{3 \cos A+\cos 3 A}{4}$

Solved Examples

For better understanding, find the multiple angles of given angles.

Q 1. What will be the multiple angle of X?

(A) 2D

(B) 5G

(C) 2X

(D) 4B

Ans: (C) 2X

In the question X is the angle. So, obviously multiple angle of "X" will contain "X" in the answer. In the options given above only the option "(C)" contains "X" . So it will be the answer.

Q 2. What will be the multiple angles of D?

(A) 2D

(B) X

(C) 2X

(D) 4B

Ans: (A) 2D

In the question D is the angle. So, obviously multiple angle of "D" will contain "D" in the answer. In the options given above only the option "(A)" contains "D" . So it will be the answer.

Q 3. What will be the multiple angle of B?

(A) 2D

(B) X

(C) 2X

(D) 4B

Ans: (D) 4B

In question B is the angle. So, obviously multiple angle of "B" will contain "B" in the answer. In the options given above only the option "(D)" contains "B" . So it will be the answer.

Practice Questions

Q 1. What will be the multiple angles of G?

Ans: 2G

Q 2. What will be the multiple angle of Z?

Ans: 2Z, 3Z, 4Z

Summary

So in this chapter you got to know about trigonometry and multiple and submultiple angles formulas in a very easy way. Also, we learned about the quadrants in trigonometry, what they are and how to name them along with the trigonometric tables and ratios. We further learned about them by solving numerous questions and practicing along with some solved examples. By solving questions, you can develop a keen understanding of the topic, which will further help you with trigonometry ahead in higher classes.