How to Find Equivalent Fractions?

How does one present the parts of an object or number in Math? How do you determine when an object has been divided in half or a quarter? This is done using the concept of Fractions. Fractions represent parts of a whole. For example, half of a quantity or an object is represented as $\dfrac{1}{2}$ in fractional form.

Fractions consist of a numerator (the number on the top half) and a denominator (the number on the bottom half). Equivalent fractions are fractions that represent the same value after they have been simplified.

What are Equivalent Fractions?

They can be defined as fractions that have different numerators and denominators from one another but represent the same amount of a whole. For example, $\dfrac{1}{3}$ and $\dfrac{4}{12}$ are equal as they both represent one-third of a whole.

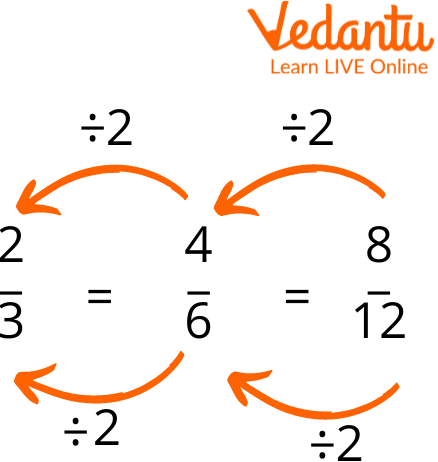
Reducing Fractions into Their Simplest Forms

Let us take a look at the image below. It has 4 circles, with each circle having some parts shaded. The first circle has one line running down it, dividing it into 2 parts. The second one has 2 lines dividing the circle into 4 parts. The third circle has 3 lines dividing it into 6 parts, and the last circle has 4 lines dividing it into 8 parts.

However, even as the number of parts increases, the amount of area shaded does not. The area shaded in the first circle is equal to the area shaded in the 4th circle even though the first circle has two divisions while the fourth circle has 8! When put in the fractional form $\dfrac{1}{2}$ and $\dfrac{4}{8}$ do not look the same, $\dfrac{4}{8}$ but can be simplified $\dfrac{1}{2}$ into.

Here is an equivalent fractions chart.

Equivalent Fractions Chart

Thus, equivalent fractions are fractions that represent the same portion of the whole.

How to Find Equivalent Fractions?

The simplest way to find the equivalents is by multiplying the denominator and the numerator of the fractions by the same non-zero number.

For example, to find the equivalent $\dfrac{6}{7}$ fraction, we can multiply the fraction by a non-zero number such as 3.

Upon multiplication, we get a new fraction $\dfrac{18}{21}$.

• $\dfrac{6}{7}$ and $\dfrac{18}{21}$ are equivalent fractions as they both represent the same partitions.

Finding Equivalent Fractions Through Multiplication

Another method that can be used to find equivalent fractions is simple division. If you divide the numerator and the denominator of a fraction with the same non-zero number, you get an equivalent fraction.

Finding Equivalent Fractions Through Division

For example, to find an equivalent fraction of $\dfrac{5}{35}$, we can divide the fraction by a non-zero number such as $5 .$

After division, we get a new fraction $\dfrac{1}{7}$.

• $\dfrac{1}{7}$ and $\dfrac{5}{35}$ are equivalent fractions as they both represent the same partition.

Thus, using either of the ways, when equivalent fractions are reduced or simplified, they will all have the same numerator and denominator. They will all be equal.

Tips for Finding Equivalent Fractions

• Multiply both the numerator and denominator with small numbers such as 2, 3, or 5.

• Never multiply or divide by 1.

• If the fraction does not have 1 as a numerator when dividing, try to see if the denominator is divisible by the numerator.

• Divide with small numbers such as 2, 3 or 5.

Solved Examples

Q1. Find 2 equivalent fractions for the fraction $\dfrac{12}{15}$ .

Ans: $\dfrac{24}{30}: \dfrac{4}{5}$

How to solve:

First, we will see if the denominator (15) and the numerator(12) have a common factor.

3 is a common factor for the two.

• Now we will divide the whole fraction by 3.

$\dfrac{12}{15} \div \dfrac{3}{3}=\dfrac{4}{5}$

Thus $\dfrac{4}{5}$ an equivalent fraction of $\dfrac{12}{15}$

• Now we will multiply the fraction by 2

$\dfrac{12}{15} \times \dfrac{2}{2}=\dfrac{24}{30}$

Since $\dfrac{24}{30}$ can also be simplified into: $\dfrac{4}{5}$ it is also an equivalent fraction of $\dfrac{12}{15}$

Thus, equivalent fractions $\dfrac{12}{15}$ of are: $\dfrac{4}{5}$ and $\dfrac{24}{30}$

Practice Questions

Q1. Find the equivalent fractions of the following.

1. $\dfrac{1}{2}$ (Ans:$\dfrac{1}{4}$ )

2. $\dfrac{15}{12}$ (Ans:$\dfrac{10}{8}$ )

Q2. Are the following equivalent fractions? Show how.

1. $\dfrac{1}{5}$ and $\dfrac{7}{35}$ (Ans: Yes)

2. $\dfrac{9}{36}$ , $\dfrac{4}{16}$ and $\dfrac{15}{65}$ (Ans: No)

Summary

Fractions represent parts of a whole. Fractions consist of a numerator (the number on the top half) and a denominator (the number on the bottom half). Equivalent fractions are fractions that represent the same value after they have been simplified. To find equivalent fractions of a given fraction, the numerator and the denominator of the given fraction need to be divided or multiplied by the same non-zero number. How we can find a fraction is explained in detail through different processes.