Introduction to Decimal Division
Decimal division is similar to dividing whole numbers, but a decimal point is inserted after each decimal place. Mathematicians divide decimals similarly to how they divide whole numbers. We must first understand what decimals are and what decimal points mean before we can understand the decimal division method.
A decimal is a numeric type that has two parts separated by a decimal point: a whole and a fraction. It is called a decimal point because it resides between parts of whole numbers and fractions. Furthermore, these numbers can be added to, subtracted from, multiplied, and divided with various arithmetic operations.
How are Decimals Divided?
Dividing Decimals
As we divide whole numbers, we also divide decimals, except the way the decimal point is handled is different. Decimals can be divided in the following ways:
Calculating decimal division by whole numbers.
Divulgation of a decimal by another decimal.
Ten, one hundred, and a thousand decimal divisions.
How Do Decimals Work?
A fractional point (also called a 'decimal separator') separates the whole part from the fractional part of a number with a point or a dot. However, in the UK, children are taught to write a point as the decimal separator, as opposed to a comma. To help children understand decimal numbers, the connection between decimal numbers and fractions will be discussed in the next section.
How to Do Decimal Division?
The whole number and fractional part of a decimal number are separated by a dot. Decimal points are the dots in decimal numbers. A value less than one appears after the decimal point. This is termed as the basic decimal division rules.
A decimal number of 17.48 features 17 as the whole number and 48 as its decimal part.
In this way here, we can use decimal division rules to find the division.
Dividing Decimals by Whole Numbers
Mathematicians divide decimals according to certain rules. The examples below show how dividing decimals by whole numbers can be done.
24 Divided by 120.6
In this case, 120.6 ÷ 24 = 5.025
Division by Five: 230.5 Divided by 5
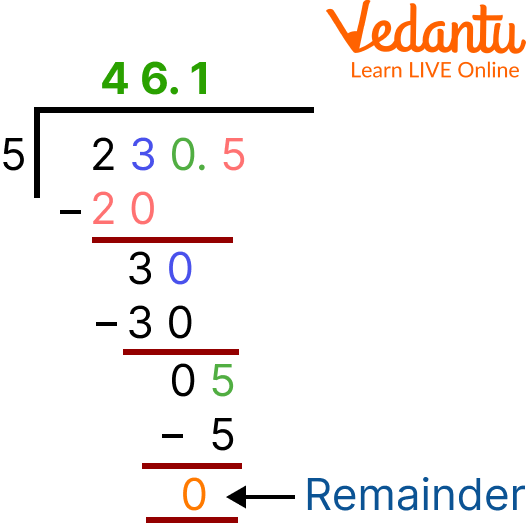
5 Divided by 230.5
The answer is 46.1 since 230.5 x 5.
The formula for dividing a decimal number by another decimal number is: When we divide numbers, we've to convert the divisor to a whole number by removing the decimal point to the right. Again, we remove the decimal point up the even number of points to the right. This can be deduced with the help of the following sample.
Example: Divide 4.88 by 0.4
Example: 15 divided by 0.2
When we multiply 0.2 by 10, we get a whole number
0.2 × 10 = 2,
But we must go to the 15
15 × 10 = 150
Thus, 15 ÷ 0.2 can be written as 150 ÷ 2
150 ÷ 2 = 75
And so the answer is
15 ÷ 0.2 = 75
Dividing Numbers by 10, 100, and 1000
Dividing Decimal by 100
Dividing numbers by 10, 100, and 1000 leaves us to find the division of a decimal Consider the number 97.5 10 = 9.75. Thus, the digits in 97.5 and 9.75 are the same, i.e., 9, 7, and 5, but the decimal point in the quotient has shifted (to the left). As a result, when dividing a decimal by 10, the decimal point will shift to the left by one position because 10 has only one zero above 1.
We may conclude from the preceding example that when dividing decimals by 10, 100, or 1000, the number and quotient digits will be the same. However, the decimal point in the quotient shifts to the left by the number of zeros greater than one.
Practice Problems
Q1. $69.27 \div 0.3 ?$
Ans: 230.9
Q2. $1.329 \div 0.06 ?$
Ans: 22.15
Summary
Thus, in this article we learnt about the decimal division. The decimal division is similar to dividing whole numbers, except for how we handle the decimal point. In addition, we learned the lengthy system of dividing decimal numbers. With the help of some examples, we learnt the division of decimals by whole numbers. We have also learned the long division styles to divide.
FAQs on Decimal Division
1. What is the step-by-step method for dividing decimals?
To divide decimals by whole numbers, follow these steps:
The division expression should be written in standard form as the first step.
The divisor must be divided by the decimal number's whole number part.
Bring down the tenth digit in the quotient after placing the decimal point above the dividend's decimal point.
In step 4, if the result's tenth digit cannot be divided by the divisor, write 0 in front of it and the quotient. If not, continue with the division process.
As you repeat steps 4 and 5 above, keep adding the zeroes to the dividend until you have a remainder of 0.
2. What are decimal numbers?
Numbers that are not whole are written with decimals. Numbers between whole numbers are decimal numbers. This can be illustrated by the decimal number 12.5, which falls between 12 and 13. The number exceeds 12 but falls below 13. Despite their different expressions, decimal numbers are just like fractions.
3. Where are decimals used?
We use decimals when dealing with money, weight, length, etc. Decimal numbers are employed when greater precision is required than whole numbers can provide. For example, when we weigh ourselves on the scale, we do not always find that the weight equals a whole number; it is usually in decimal form.
