




How to Recognize and Use Fractions in Everyday Life
A fraction has two parts, a numerator, and a denominator. In simple words, a fraction of anything is a part of the whole thing. For example, an apple is cut into 8 equal pieces and you share it with your friend. Now, if your friend eats 3 pieces and you eat the remaining 5 pieces, then what fraction of the apple do you consume? The number of pieces you eat will be the numerator of the fraction and the total number of pieces will be the denominator.
Thus, the fraction of the apple eaten by you is $\frac{5}{8}$ and that eaten by your friend is $\frac{3}{8}$. Interestingly, if you add these two fractions, $\frac{5}{8}$ and $\frac{3}{8}$, you will get the sum to be 1. In simple words, 1 whole apple is divided into two fractions $\frac{3}{8}$ and $\frac{5}{8}$. Therefore, we can say, that all fractions representing a particular thing will add up to 1 representing the whole thing.
In the following sections, the concept of a unit fraction, denominator, numerator, and number line are explained. Once you will be familiar with these concepts only then you will be able to solve sums on fractions.
Fractions: Related Terminologies
Some terminologies related to Fractions for year 3 are given below.
Fraction: As stated above, fraction is defined as a part of a whole. To express something in fractions, the whole thing has to be divided into several equal parts.
Numerator: A fraction has two parts, rather two digits, one written on the top of a horizontal bar while the other written below it. A numerator is a number or the digits placed above the bar in a fraction, it represents how many equal parts of the whole are being considered for a given scenario.
Denominator: A denominator is the number or digits written below the bar in a fraction. It represents how many equal parts are present in the whole.
Example: Let's suppose you have one slice of pizza that has a total of four slices. If you have eaten one slice then there will be three slices of pizza remaining. Hence it can be written as $\frac{3}{8}$where 3 represents how many parts are left and 4 represents how many equal parts is the whole pizza divided into. So here 3 is the numerator and 4 is the denominator.

Numerator and Denominator
Unit Fraction: A unit fraction is a fraction having a numerator of value 1. For example, $\frac{1}{7}$.
Non-unit Fraction: A non-unit fraction is any fraction with a numerator greater than 1. An example of the non-unit fraction is $\frac{3}{4}$.
Proper fraction: A proper fraction is a fraction in which the numerator is less than the denominator, thus the value of the fraction is less than the whole. For example, $\frac{3}{4}$, $\frac{2}{11}$ and $\frac{7}{19}$ are proper fractions.
Improper fraction: An improper fraction is a fraction in which the numerator is greater than the denominator, thus the value of the fraction is greater than the whole. For example, $\frac{5}{2}$, $\frac{8}{5}$ and $\frac{12}{11}$are improper fractions.
Number Line: A visual image used in almost all classrooms to help children grasp basic number relationships. The denominator indicates the total number of parts the number line must be divided into. For example, if the denominator is 4 then we need to create 4 equal parts between 0 and 1. We mark these parts with short vertical lines. The number line drawn below is divided into four parts of equal length.
Number Line from 0 to 1.
The numerator is the number of parts being considered. We always start counting from 0.
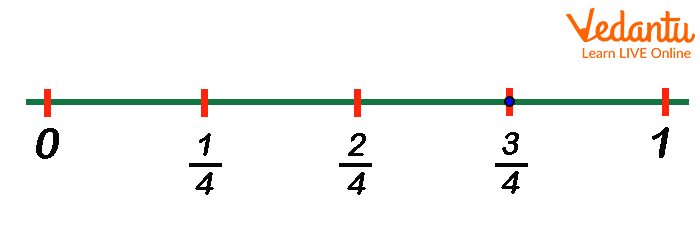
Partition of number Line
Some examples of fractions are marked on the number line. Now see these examples and analyse how they are marked.

Examples of different Fractions on Number Line
Conclusion
The above information explains some terms related to fractions that are important for kids of the age group 7-8 years as they will grab the advanced concept of fractions when they’ll be familiar with these terminologies. Solve and practice fractions for year 3 worksheets to get a better understanding of the concepts of fractions discussed above.
FAQs on Fractions Made Simple for Year 3 Children
1. What are the numerator and the denominator of a fraction?
A fraction consists of two parts. These parts are the numerator and the denominator. The number or digits written on the top of the horizontal line is called the numerator. It is used to indicate the number of parts of the whole thing being considered. The number or digits that are written below the horizontal line is known as the denominator. For example, $\frac{3}{7}$ is a fraction number where 3 is the numerator and 7 is the denominator.
2. Give some real-life examples of fractions.
We know that fractions are an important part of our daily lives because we are able to get an idea of what portion of a whole is required, have, or want by doing some calculations of fractions. The real-life example of uses of fractions can be seen in baking, cooking, shopping etc. It is used to tell time as each minute is a fraction of an hour. When we go to buy household things or any material used in cooking things are often sold in a fractions of units.

















