Fraction in Lowest Term - Learn an Easy Way to Simplify Fraction into Its Lowest Term

Fractions are numerical values that are used to represent any number of equal parts of a whole. Fractions are real numbers, represented in the form of ab. Here, both a and b are integers. The number written at the top i.e. above the horizontal bar is termed as numerator whereas the number written at the bottom i.e. below the horizontal bar is termed as denominator.

What Do the Terms Numerator and Denominator Mean in Fraction?

The top number in a fraction i.e. numerator shows the total number of parts we have. Whereas the bottom number in a fraction i.e. denominator shows the number of parts an object or item is divided into.

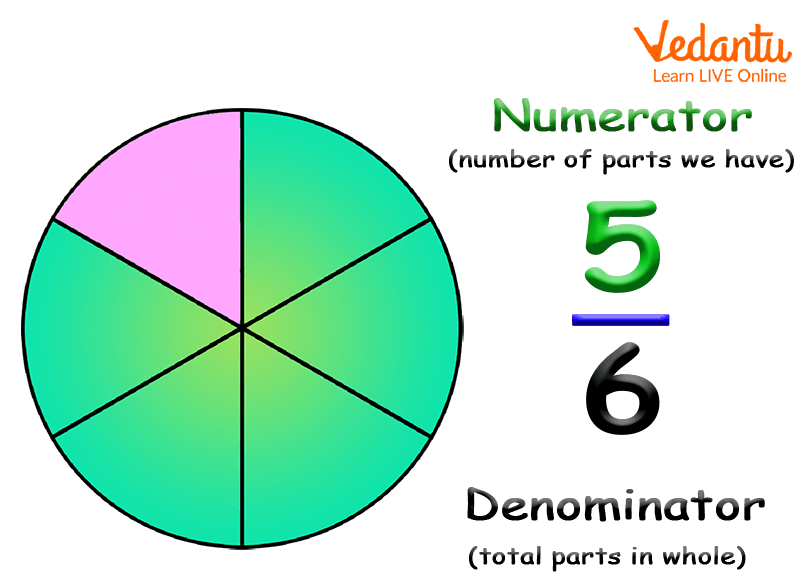
Fraction Example.

In the above image, fraction $\frac{5}{6}$ is read as “five sixths”. Here, the numerator 5 represents the number of parts we have and the denominator 6 represents the total number of equal parts in a whole.

What Does Fraction in Lowest Term Means?

A fraction is said to be written in the lowest term if its numerator and denominator are relatively prime numbers, i.e. they have no common factors other than 1. In other words, a fraction is said to be in its lowest terms or lowest form, if the HCF of the numerator and denominator is 1.

For example, $\frac{5}{3}$ is written in lowest, as both numerator and denominator have no common factors other than 1. Also, the HCF of 5 and 3 is 1.

On the other hand, $\frac{6}{3}$ is not written in its lowest term as both numerator and denominator have a common factor 3.

How to Reduce Fraction in its Lowest Term?

There are two different methods to reduce fractions in its lowest term. Let us understand both the methods with an example.

Method 1: HCF or Highest Common Factor Method

In order to reduce the fraction in its lowest term, we will divide its numerator and denominator by their HCF. 

For example, if we reduce $\frac{21}{56}$ into its lowest term, we will follow the given steps.

• Step 1: We will first find the HCF of the numerator and denominator i.e. 21 and 56.

HCF of 21 and 56

Therefore, the HCF of 21 and 56 is 7. 

• Step 2: Now, we will divide both numerator and denominator by its HCF as shown below

$\frac{21÷7}{56÷7}$ =  $\frac{3}{8}$

Therefore, $\frac{21}{56}$ in its lowest term is written as $\frac{3}{8}$.

Now, let us solve a problem to understand it better. 

1. Reduce $\frac{48}{64}$ into its lowest term using the HCF method.

Solution:

• Step 1: We will first find the HCF of the numerator and denominator i.e. 48 and 64. Here, we will find the HCF of 48 and 64 using the factorisation method. Let us find the factors of 48.

Factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.

Factors of 64 are: 1, 2, 4, 8, 16, 32, and 64.

The common factors of 48 and 64 are: 1, 2, 4, 8, and 16.

Therefore, the HCF or highest common factor of 48 and 64 is 16.

• Step 2: Now, we will divide both numerator and denominator by its HCF as shown below:

$\frac{48÷7}{64÷16}$ =  $\frac{3}{4}$

Therefore, $\frac{48}{64}$ in its lowest term is written as $\frac{3}{4}$.

Method 2: Prime Factorisation Method

In order to reduce the fraction to its lowest term using the prime factorisation method, we will first find out the prime factors of the numerator and denominator and cancel out their common factors.

For Example:

1. Reduce $\frac{120}{160}$ into its lowest term using the prime factorisation method.

• Step 1: We will first find the prime factors of 120 and 160.

Therefore, 

The prime factors of 120 are: 2 2 2 3 5

The prime factors of 160 are: 2 2 2 2   2 5

• Step 2: Now, we will cancel out the common factors. Common factors are the factors that appear in both the numerator and denominator. In this example, we will cross our three 2’s and one-time 5 from both top and bottom as their common factor. The remaining 3 in the numerator and two 2’s are not the common factors. So, we will not cross out one 3 from the numerator and two 2’s from the denominator.  

$\frac{120}{160}$ = $\frac{2*2*2*3*5}{2*2*2*2*2*5}$

Therefore, $\frac{120}{160}$ in its lowest term is written as $\frac{3}{2*2}$ = $\frac{3}{4}$

Conclusion

In short, a fraction can be written in its lowest term or simplest form, if both numerator and denominator have no common factor other than 1. HCF method and the Prime Factorisation method are the two different methods to reduce fractions in their simplest or lowest form. In other words, to reduce the fraction in its lowest term, either divide both numerator and denominator by their HCF or find out the prime factors of both numerator and denominator separately and cancel out the common factors between them.