Divisibility Rule of Number 8

The relation between divisor, dividend, quotient, and remainder must be known first.

Dividend = Divisor × Quotient + Remainder

A number is said to be divisible by another number if the remainder is zero after dividing.

For Example: If 4 is divided by 2, the remainder will be zero. So, it can be said that 4 is divisible by 2. Here, it can be written as 4= 2 x 2 + 0

Let's think about a large number like 9895763648798. Can you tell if it is divisible by 2 without actually dividing it?

Observe, carefully in 9895763648798, the last digit is 8. 8 is divisible by 2 therefore, the whole number is divisible by 2. How easy it became to tell the answer with a simple rule.

Imagine, if there is any number and you need to check the divisibility with another number, with the help of some rules you can give the answer without actual division. Such rules are known as divisibility rules.

What are Divisibility Rules?

Divisibility rules are a set of general rules used to check whether a number is divisible with the other number or not.

For Example: If a number is even that must be divisible by 2.

Here, we will learn how to check whether a number is divisible by 8 or not.

What is the Divisibility Rule of the Number 8?

If the number formed by the last three digits of the given number is divisible by 8, then the given number is also divisible by 8.

Let’s see the divisibility rule of 8 with an example.

Example 1: 6,920

Step 1: last three digits of 6,920 = 920.

Step 2: check whether 920 is divisible by 8 or not.

Division (6,920 )

Since remainder = 0, therefore 920 is divisible by 8,

Which means the given number, i.e. 6,920, is also divisible by 8.

Let’s take another example.

Example 2: 15,016

Step 1: last three digits of 15,016 = 016 = 16,

we know 16 is divisible by 8,

Which means the given number, i.e. 15,016, is also divisible by 8.

THINK

Think

We know that 0 is divisible by every number

0/8 = 0

So, in that case, the number will be divisible by 8.

Let’s understand this better with an example

Example 3: 97,000

Step 1: last three digits of 97,000 = 000 = 0,

And we know 0 is divisible by 8

So, 97,000 is also divisible by 8.

Let’s check this number by division method also for better understanding.

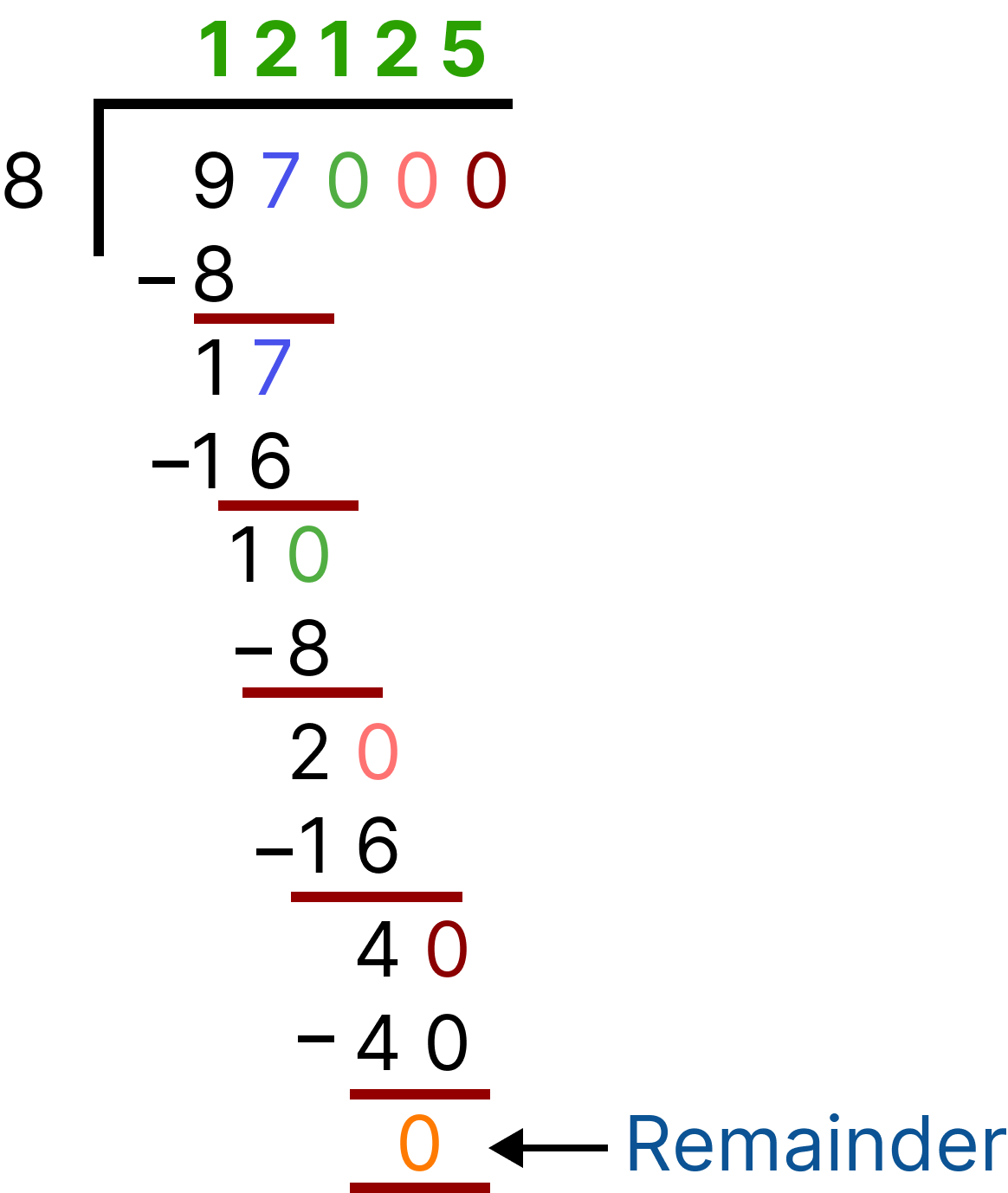
Division (97,000)

Solved Examples:

Q1. Check, Which number is divisible by 8?

Ans:

Let’s solve these by both methods( by division and divisibility rule of number 8 as well)

1. 67,060 /8

Division(67,060)

Now, check by divisibility rule, last three digits are 060

We can see that the last three-digit is not divisible by 8, therefore 67,060 is not divisible by 8.

2. 8008/8

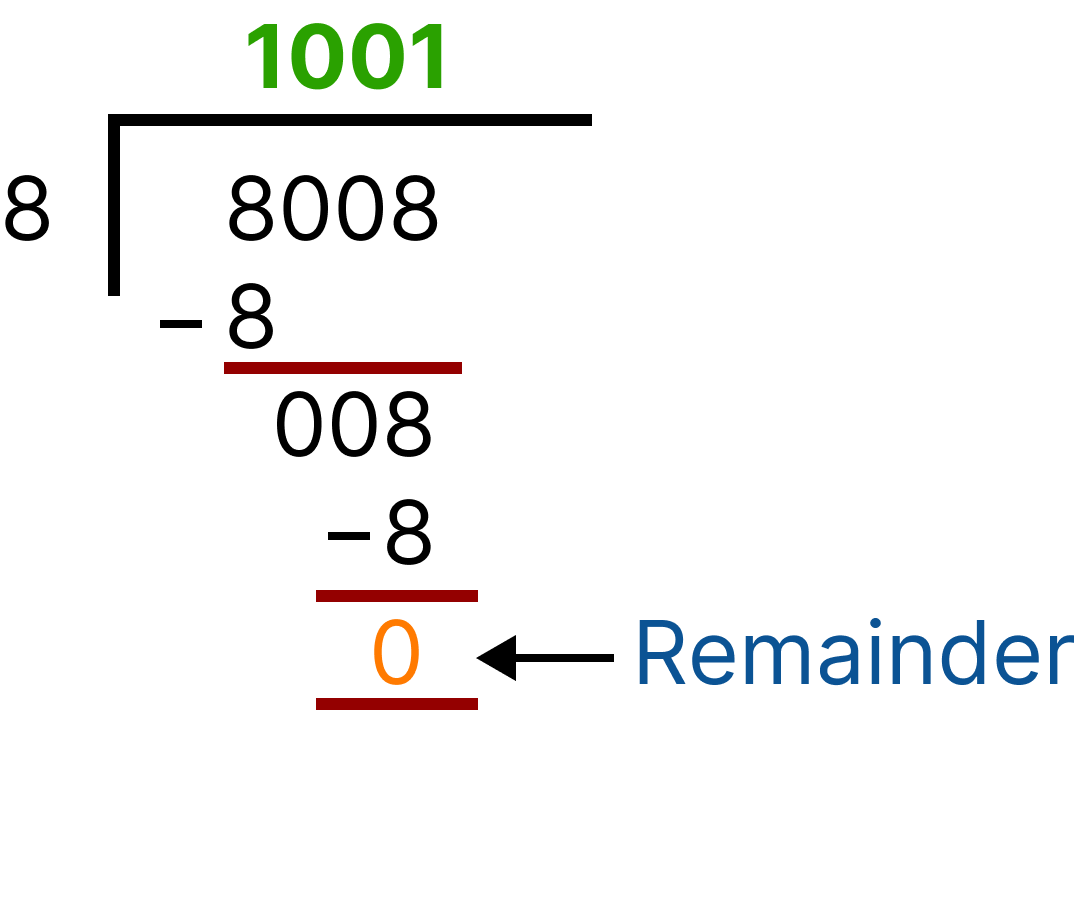
Division (8008)

Now, check by divisibility rule, last three digits are 008

008 is divisible by 8, therefore 8008 is divisible by 8

3. 687816/8

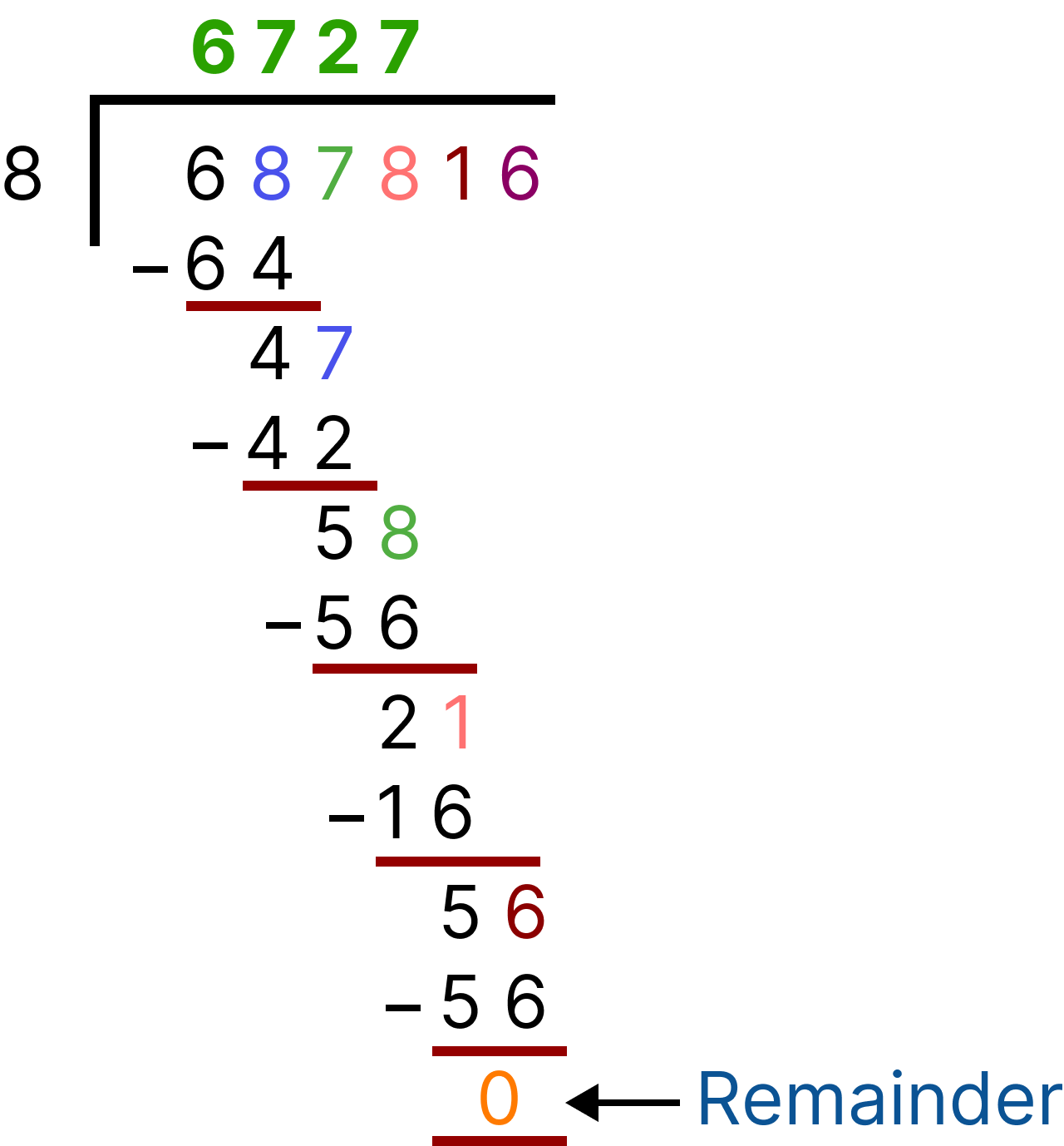
Division (687816)

Now, check by divisibility rule, last three digits are 816

816 is divisible by 8, therefore 687816 is divisible by 8.

4. 7407/8

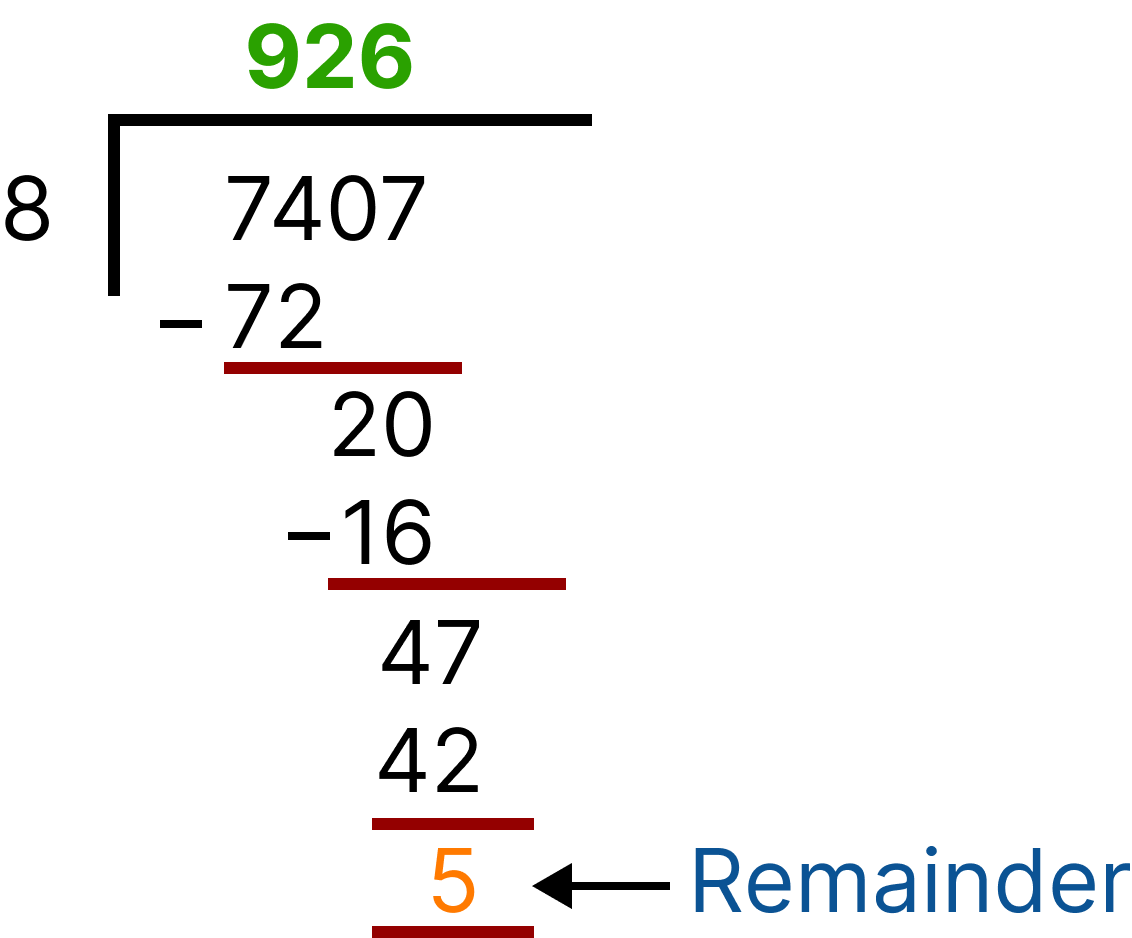
Division (7407)

Now, check by divisibility rule, last three digits are 407

407 is not divisible by 8, therefore 7404 is not divisible by 8.

5. 345,000/8

Division (345,000)

Now, check by divisibility rule, last three digits are 000

000 is divisible by 8, therefore 345,000 is divisible by 8.

6. 98,512/8

Division (98,512)

Now, check by divisibility rule, last three digits are 512

512 is divisible by 8, therefore 98,512 is divisible by 8.

Solve the Problem

Ans:

We know odd numbers are not divisible by 8. So we’ll start placing even numbers in one's place.

Because we have to choose the smallest possible digit, let’s start with the smallest even digit, i.e. 0.

The number will become 31710

The last three digits of 31710 = 710.

Let’s check whether 710 is divisible by 8 or not?

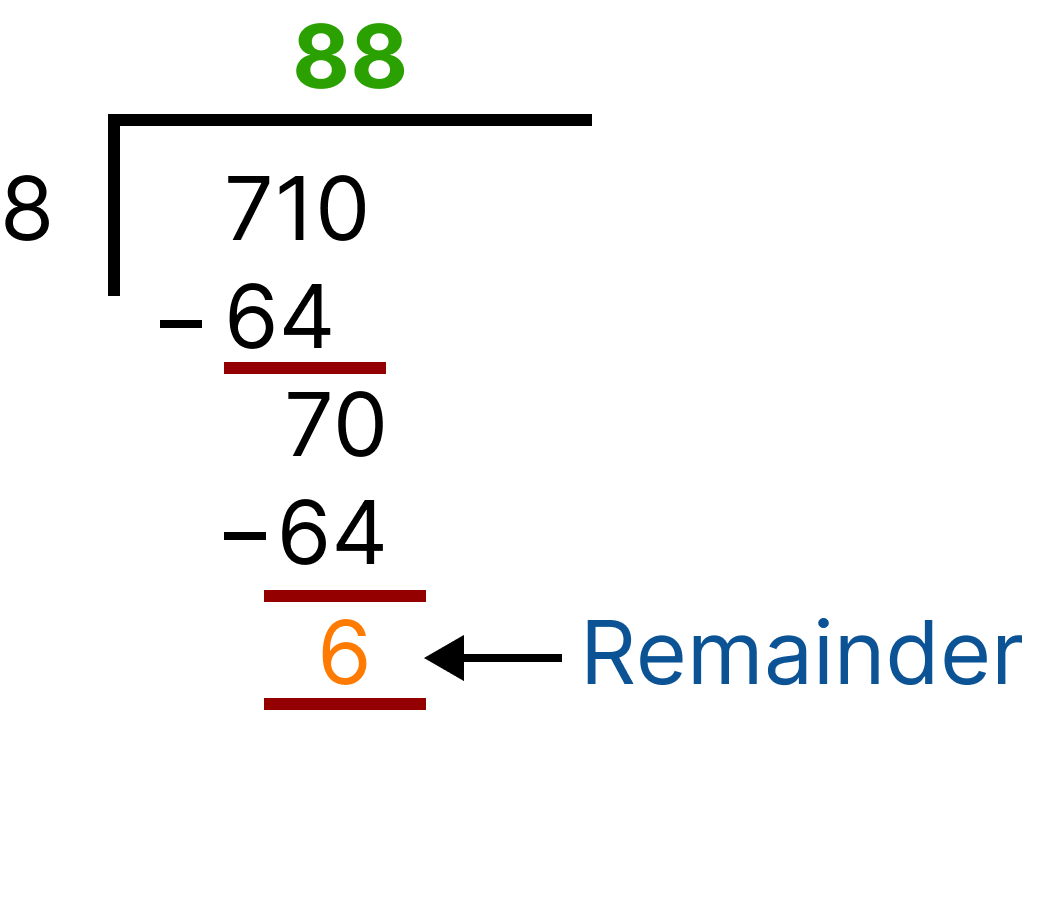
Division (710)

Remainder ≠ 0; therefore, 710 is not divisible by 8.

Let’s move to the next smallest even digit, i.e. 2, the smallest possible digit.

Last three digits of 31712 = 712.

Let’s check whether 712 is divisible by 8 or not?

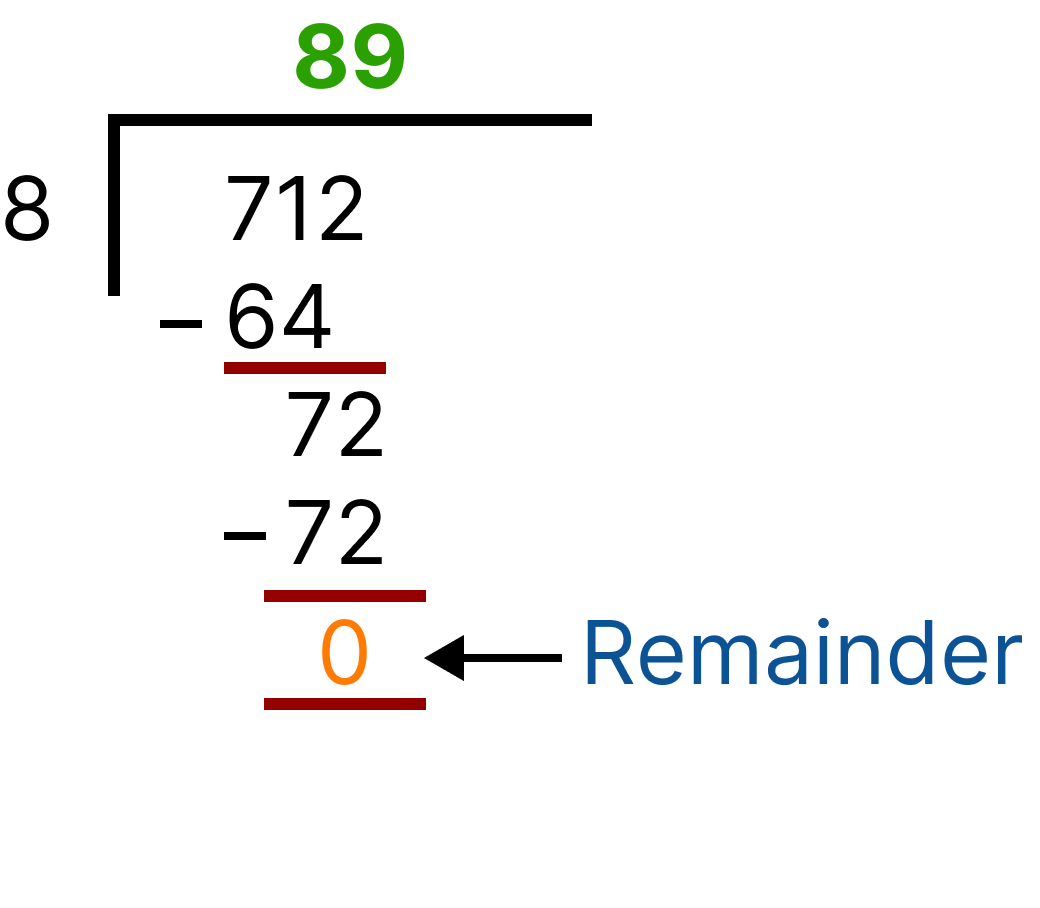
Division (712)

Remainder = 0 , therefore, 712 is divisible by 8.

So, the required number is 31712, which is divisible by 8.

Practice on Your Own:

1. Reena has 431 chocolates. Can she divide equal chocolates among her 8 friends?

Ans: No, Reena can not divide equal chocolates among her 8 friends.

2. If there are 4328 mangoes, can you distribute them in equal groups of 8?

Ans: Yes, 4328 mangoes can be distributed in equal groups of 8.

Fun Facts:

1. Every Number is divisible by 1.

2. When a number is divisible by another number, then it is also divisible by each of the factors of that number. For instance, a number divisible by 8, will also be divisible by 2 and 4 because 8 is divisible by 2 and 4.

3. If we divide zero by any number, the result will be zero.