Classifying Angles and Figures

Angles are formed when two lines intersect at a point. The measure of the 'opening' between these two rays is called an 'angle'. Angles in Mathematics are measured when we need to find the inclination of a line with respect to another line or to describe the various types of figures in geometry. We always measure the angle in an anticlockwise direction from the x-axis but if we measure the angle in a clockwise direction the measure will be equal to $180^{\circ}-\mathrm{a}$ where a is the measure in a clockwise direction. In this article, we will learn about types of angles in Maths and also the different types of figures.

What are Angles?

Angle is the measure of the inclination of a line concerning another line or an axis. The inclination of a line is always measured in an anticlockwise direction from an axis. The angle is measured in degrees and radians represented by $\left({ }^{\circ}\right)$ and $(\mathrm{rad})$ respectively. Every time two lines or two line segments intersect, it forms an angle with the other line, and two pairs of vertically opposite angles form. Let us understand this concept of angle with the help of a figure:

Angles

Types of Angles in Maths

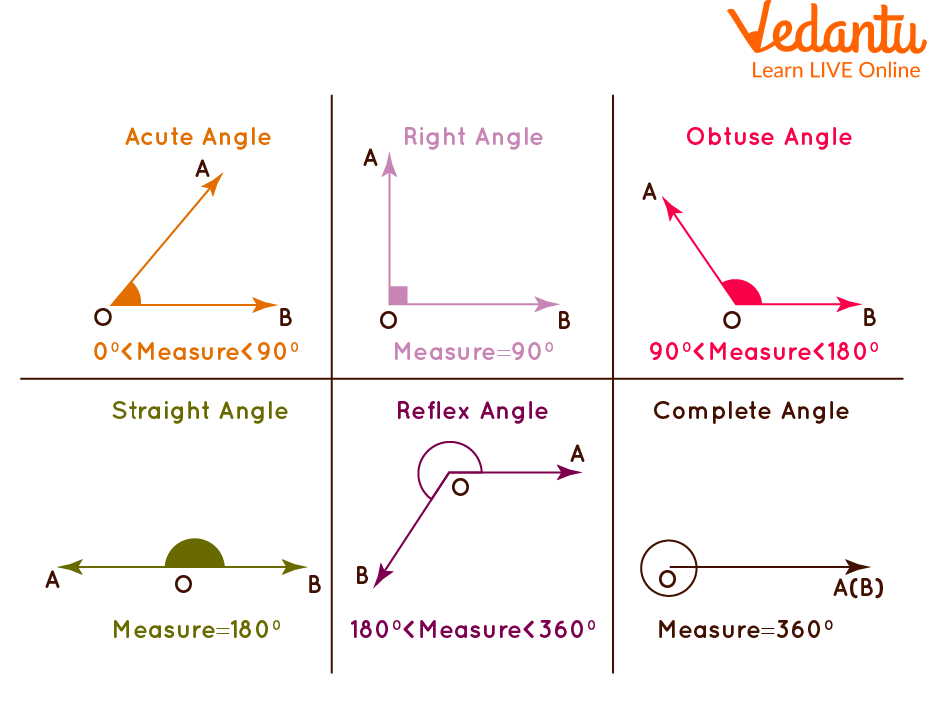
Angles can be classified into 3 types and they are right angle, acute angle, and obtuse angle.

Let us understand each one of these in significant detail:

Acute angle: The angle which has its measures less than 90⁰ or any angle which is less than 90⁰ is known as the acute angle.

Acute Angles

Obtuse Angle: The angle which measures more than 90⁰ or any angle which is more than 90⁰ is known as an obtuse angle.

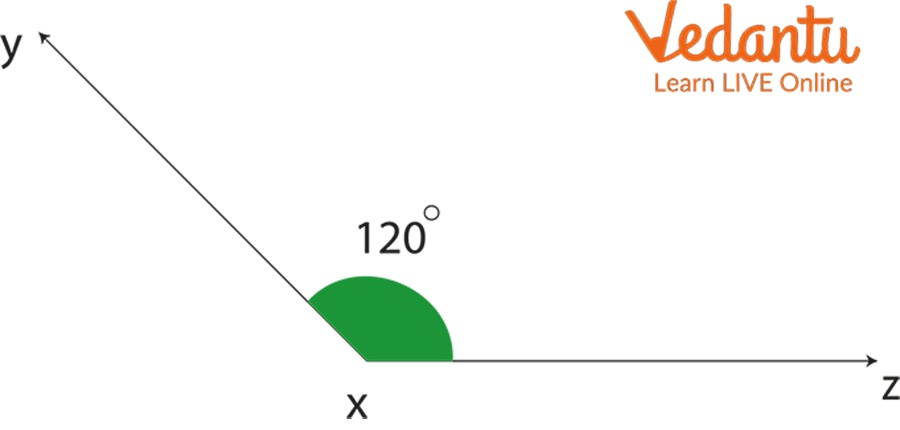
Obtuse Angle

Right Angle: The angle which has a measure of 90⁰ is known as the right angle.

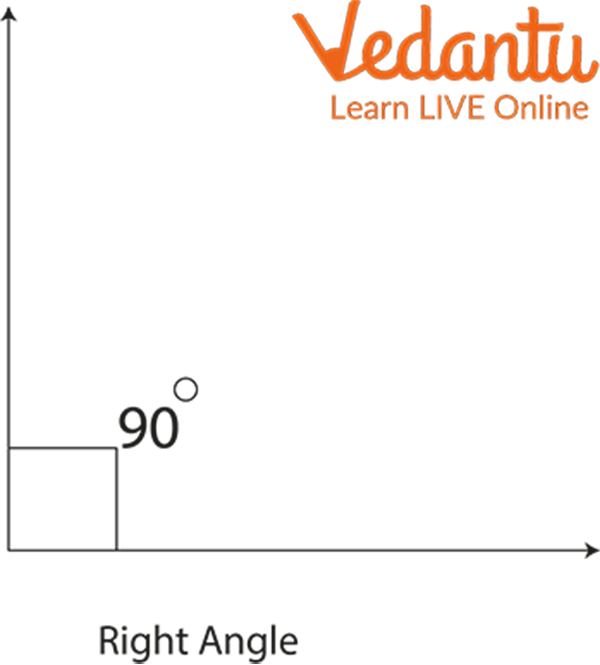
Right Angle

What are Figures?

Figures in a plane are said to be plane figures. It means if a figure can be drawn in a single plane then it is said to be the plane figure. There are various geometrical figures in Mathematics. To form a figure, a minimum of three lines are required. By varying the angle and increasing the number of sides, different plane figures are obtained namely square, rectangle, pentagon, hexagon, etc.

Different Plane Figures

Square: It is a plane figure which has four sides and all four sides are equal in length. The area of the square is given by squaring the length of one of its sides i.e.,

Area $=(\text { Side })^2$

The perimeter of the square is $=4 \times$ the Length of one side.

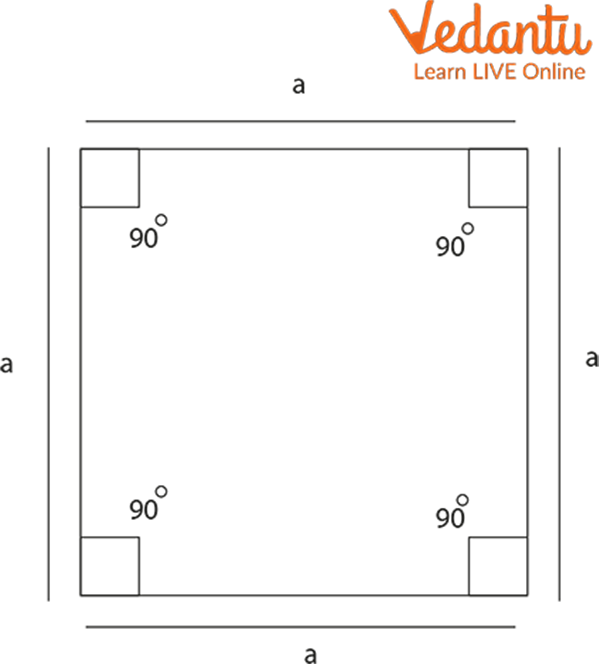
Square

Rectangle: It is a plane figure which has four sides but the length of opposite sides is equal and length of adjacent sides is unequal.

The area of the rectangle is $=$ Length $(\mathrm{I}) \times$ Breadth $(\mathrm{b})$

The perimeter of the rectangle is the sum of all four sides i.e.,

$=2 \mathrm{l}+2 \mathrm{b}$

$=2(l+b)$

Rectangle

Triangle: It is a plane figure which has three sides.

The area of triangle is = \[\frac{1}{2}\] x base x hieght

The perimeter of the triangle is = Sum of the length of all the three sides

Triangle

Parallelogram: It is a plane figure which is bounded by four sides and the opposite sides are parallel and equal but the vertex angle is not equal to 90⁰ which is in the case of square and rectangle.

The parallelogram which has all the sides equal is known as Rhombus.

Area of Rhombus $=\dfrac{1}{2} \times d_1 \times d_2$;

where $d_1$ and $d_2$ are the two diagonals of the rhombus.

If the adjacent sides of the parallelogram are parallel and equal then the area = base × altitude; where the base is one of the sides of the parallelogram and altitude is the perpendicular distance between the base and the opposite sides.

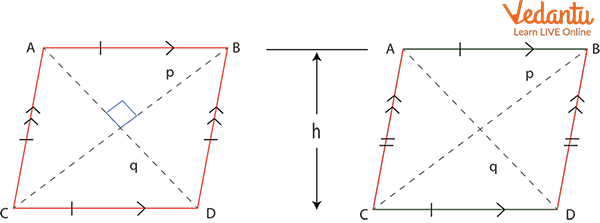
Rhombus and Parallelogram

Circle: It is a plane figure which is represented as below:

Circle

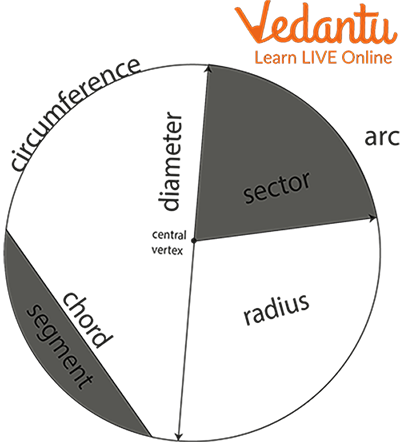
Area of circle $=\pi r^2$

The perimeter of the circle is $=2 \pi r$; where $r$ is the radius of the circle and the value of $\pi$ is taken to be $3.14$ or $\dfrac{22}{7}$.

Solved Examples

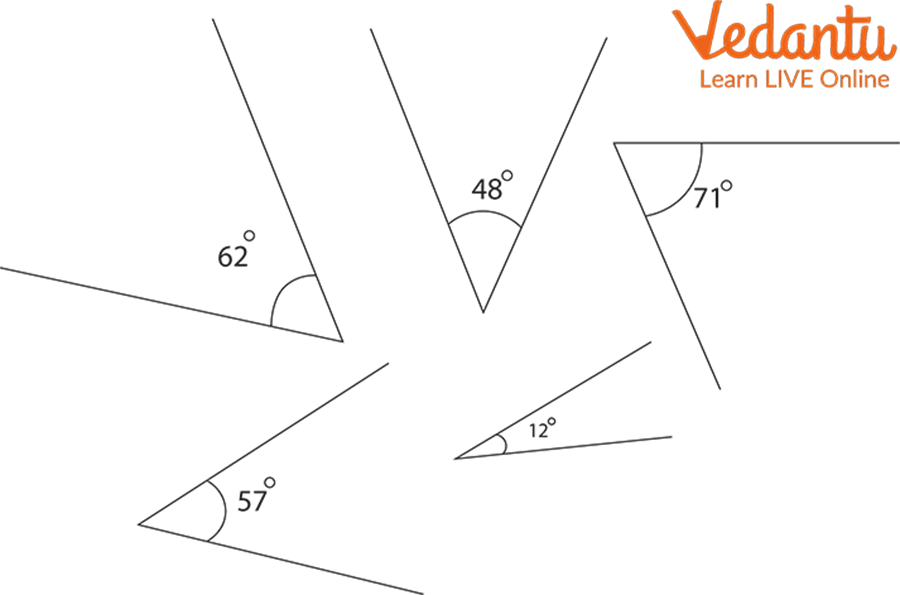
Q1. Find the value of the missing angle in the following figure:

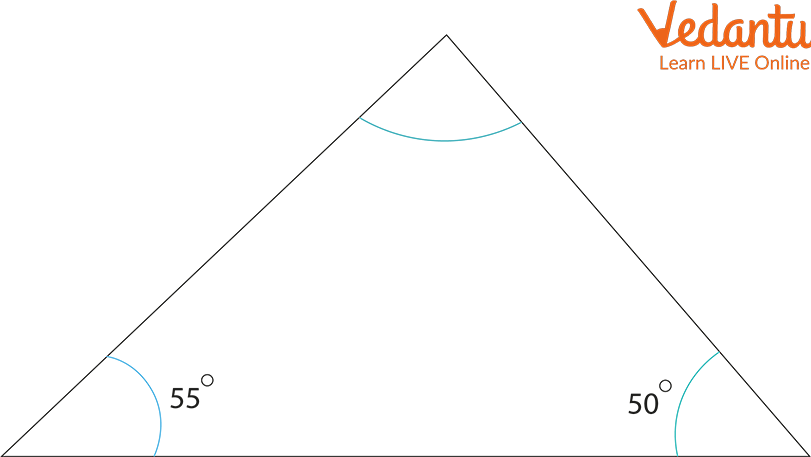
Missing Angle

Ans: We know that the sum of angles in a triangle is $180^{\circ}$.

Let the unknown angle be $x$.

Now, according to the question,

$x^0+50^{\circ}+55^{\circ}=180^{\circ}$

$\Rightarrow x^0+105^{\circ}=180^{\circ}$

$\Rightarrow x^0=180^{\circ}-105^{\circ}$

$\Rightarrow x^0=75^{\circ}$

Q2. Calculate the area and perimeter of the triangle whose base is 56 units and height is 32 units and the length of the third side is 62 units.

Ans: Given, the sides of the triangle are 56, 32, and 62 units.

The area of triangle is $=\dfrac{1}{2} \times$ base $\times$ height

$=\dfrac{1}{2} \times 56 \times 32$

$=896 \text { units }^2$

The perimeter of the triangle is $=$ (Sum of lengths of all three sides)

$=(56+32+62)$

$=150$ units.

Practice Problems

Q1. Calculate the missing angles of a parallelogram if the two adjacent angles are $135^{\circ}$ and $45^{\circ}$

Ans: $135^{\circ}$ and $45^{\circ}$ as the opposite angles of the parallelogram are equal.

Q2. What is the area of the circle with a radius of $7 \mathrm{~m}$? Also, calculate its circumference.

Ans: $154 \mathrm{~m}^2\left[A=\pi r^2\right], 44 \mathrm{~m}$.

Q3. What is the area of a rectangle whose length is 32 units and whose breadth is half of its length? Also, calculate its perimeter.

Ans: 512 units $^2$, 96 units

Summary

We have seen that there are different kinds of angles in Mathematics and that triangles can be right-angled triangles or isosceles triangles. We have also learned about plane figures and different types of plane figures. We further learned how to find the area and perimeter of plane figures. We took note of the different types of angles and the area and perimeter of figures in mathematics. We also got to know about the formation of different types of figures using different numbers of line segments and varying the angles between them.