Benchmark Fractions

What are Benchmark Fractions?

Before understanding the meaning of benchmark fractions, let us first learn what do/es the term ‘Benchmark’ mean? Benchmark can be defined as the standard or reference point against which you can measure or compare something. Whereas, Benchmark fractions are common fractions to which we can compare less common fractions. For example, if you want to compare two fractions, 15 and 27, then in such a case, by finding a benchmark which lies between the two fractions, you can compare if a fraction is greater than, lesser than, or equals to another fraction.

Benchmark Fractions

What are the most Common Benchmark Fractions?

The most common benchmark fractions are zero, one-half, and 1. Sometimes thirds or tenths are also used.

How to Compare Fractions using Benchmark Fractions?

Students often use benchmark fractions to compare fractions with different or unlike denominators. You can use benchmarks on a number line to compare fractions. Also, you can use the relationship between numerator and denominator of a fraction to compare to a known benchmark fraction and then use this information to compare the given fractions.

Let us understand with an example:

Suppose, you want to compare 47 and 25, then in such case, you can see 47 is greater than 12 ( 47 > 12) , whereas 25 is less than 12 (25 < 12). Hence, we can say that 47 > 25.

How You Can Use Benchmarks On A Number Line To Compare Fractions?

Let us understand with an example how to use benchmark fraction on a number line to compare a given fraction.

Suppose, you want to know whether 26 is greater than or less than 12, then in such a case you can draw a number as shown below.

Step 1: First draw a number line and mark it with benchmark 0, 12 and one whole or 1 as shown below.

Step 2: Now check how many sixths are there in one whole using the number line given below.

There are toal 6 sixths in one whole.

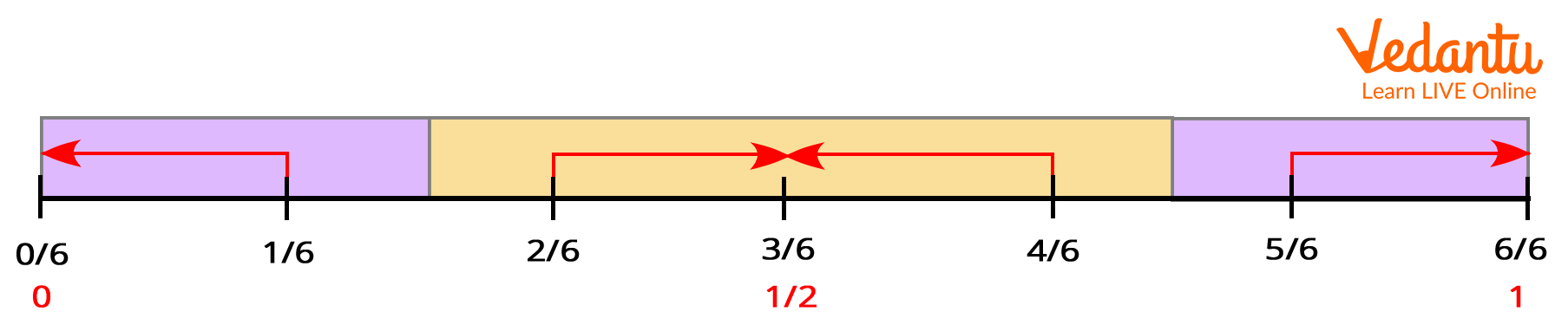
Also, we can see 36 is same as 12 in the above number line,

Now compare whether 26 is greater or lesser than 36 .

We can see 26 is lesser than 36 , because 26 is closer to 0 on a number line. And, we know a fraction is smaller if it is closer to 0 on a number line.

Accordingly, 26 <12

Benchmark Fraction Examples Using Number Line

1. Find 316 + 1259 using benchmark fraction on a number line.

Solution:

In number line below, we can see 16 is closer to 0, hence, 316 is close to 3.

In the below number line, we can see 49 is close to 12, hence, 1249 is close to 1212.

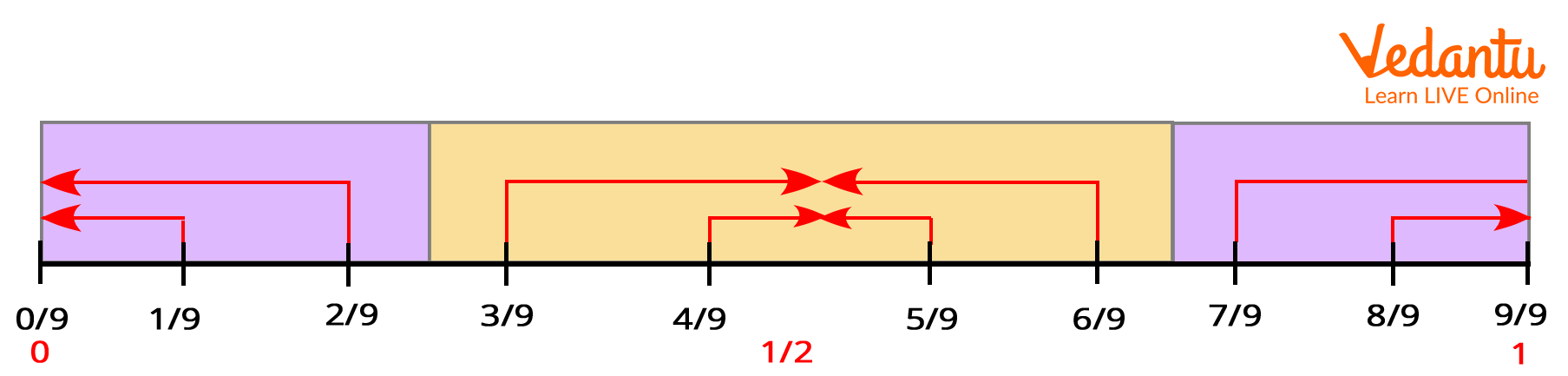
Hence, 316 + 1249 is close to 3 + 1212

Therefore, 316 + 1249 is close to 1512.

Benchmark Fraction Guidelines For Rounding Fraction

1. Round the given fraction to 0 if the numerator is much smaller than the denominator. For example: 18, 321, 417, etc.

2. Round the given fraction to 12, if the numerator is almost half the denominator. For example, 37, 613, 817, etc.

3. Round the given fraction to 1, if the numerator is nearly equal to the denominator. For example, 78, 2123, 97100, etc.

Benchmark Fraction Example For Rounding Fraction

1. Estimate 79 - 15

Solution:

Let us first round each fraction

79 is rounded to 1

15 is rounded to 0

Now subtract

1 - 0 = 1

Hence, 79 - 15 is close to 1.

2. Estimate 459 + 318

Solution:

Let us first round each fraction

In 459, 59 is rounded to 12. Hence, 459 is rounded to 412.

In 318, 18 is rounded to 0. Hence, 318 is rounded to 3.

Now Add,

412 + 3 = 712

Hence, 459 + 318 is close to 712.

Hope you have clearly understood the concept of benchmark fractions through these solved examples. You can find many more information on any math topic and solved examples on our website.