




Step-by-Step Guide to Solving Maths Questions Using Bar Models
Introduction to Bar Model
A bar model is a pictorial representation of Mathematics problems. The bar model is popularised by the Singapore teaching model and is now being increasingly used in the United Kingdom. Jerome Bruner in the 1960s introduced that people learn in three stages, namely concrete, pictorial, and abstract. The bar model is a way to support students with the middle stage, i.e., pictorial. Read below to know more about bar models.
What is a Bar Model?
Bar model, also known as tape diagram in Japan and strip diagram in the United States, is used throughout the world to help students visualise Maths problems. The main purpose of the bar model is to simply represent Mathematical problems, especially which are quite difficult to solve without visualising it first. There are several variations of the bar model, but all follow the same principles as discussed below:
Bar models are designed in a specific way, using rectangles to represent known and unknown amounts.
Bar models are designed to gather all the relevant information from a problem to examine any facts presented in the questions. This helps children to start working towards solving an answer.
It should be noted that the bar model is not a method of calculation, but in fact, it is used as a way to help children decide which Mathematical operation should be used.
Once a bar model has been developed, the children can start the calculation. This can be done using students' preferred written or mental calculation methods.
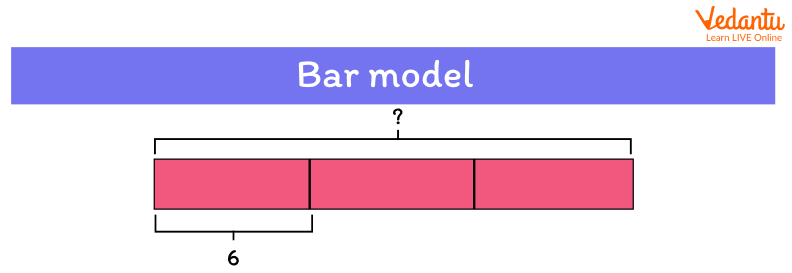
In the bar model given below, one bar or one rectangular box of the bar model represents the value of 6. Here, we have to find the 3 times the value of one bar.
Types of Bar Model
There are two types of bar models. They are:
Part-Whole Bar Model
Comparison Bar Model
Let us understand both the models briefly.
Part-Whole Model
The part-whole model, also known as the part-part whole model, is a pictorial representation of problems that help learners to observe the relationship between the numbers. A horizontal bar represents the whole amount. Below it, a similar bar is divided into pieces to represent the part of the whole.
Part whole model is further splitted into:
Discrete Part/Whole Model: In this model, each unit in the problem is represented by its own individual box, similar to using Numicon cubes. An example of discrete part/whole model is represented below:
Discrete Part/Whole Model Example:

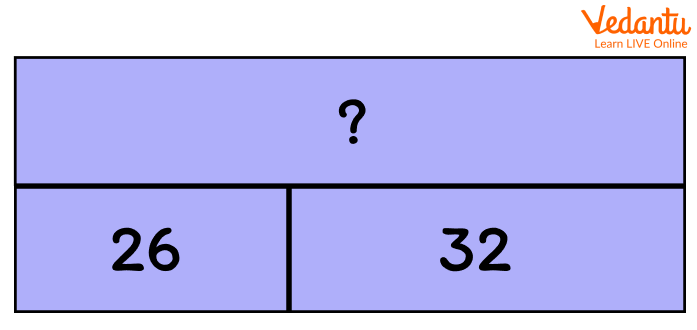
Continuous Part/ Whole Bar Model: In this model, units are grouped into one box for each amount in the problem. For example, in the problem, 26 + 32, 26 will have one longer bar, instead of having 26 small rectangles joined together.
Continuous Part/Whole Model Example
Part-Whole Model is ideal to solve:
Addition Problems
Subtraction Problems
Multiplication Problems
Division Problems
Fraction
Comparison Bar Model
Instead of having a bar which represents the whole problem, in a comparison model, two or more vertical bars are drawn to help children to compare two or more amounts. In this type of model, bars are often used to represent the whole amount.
The comparison bar model is basically used to find the difference between two amounts, helping to strengthen the ideas of using subtraction to find the difference. Here is an example of a problem and comparison bar model representation.
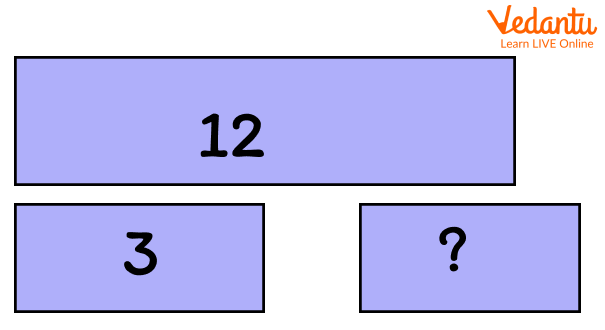
Problem: Tina has 12 playing cards and Riya has 3. How many more cards does TIna have than the Riya?
Bar Models with Four Mathematical Operations
Here are bar models representing four Mathematical operations namely addition, subtraction, multiplication, and division.
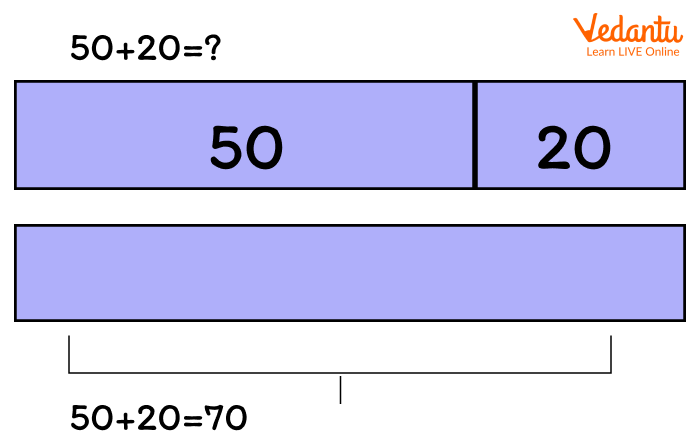
Bar Model Representing Addition
Bar Model Representing Subtraction
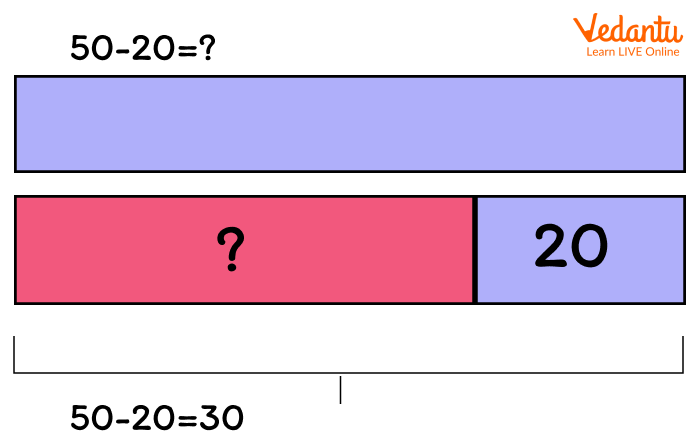
Bar Model Representing Multiplication
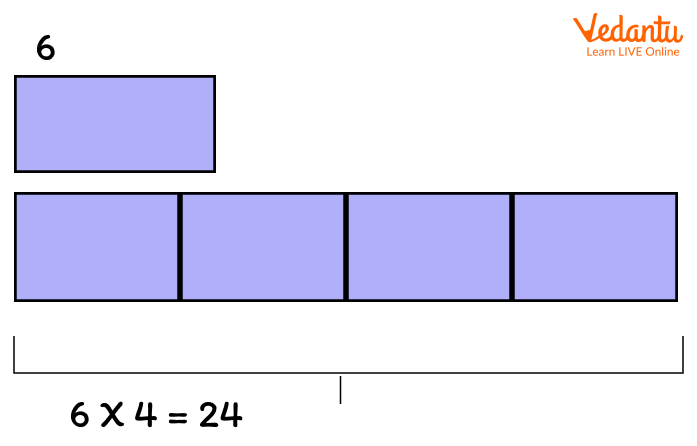
Bar Model Representing Division
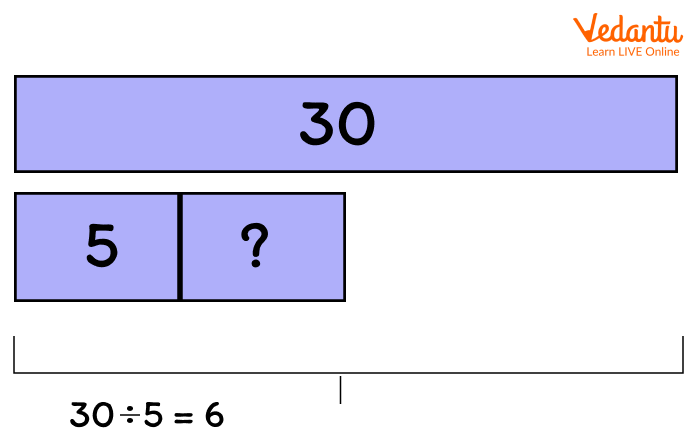
Does the Bar Model Provide an Answer?
The bar model is a visual representation to help solve problems using different sized rectangles to represent the bar. The rectangles or bars in the bar model should be proportional so that the larger number is represented by the larger number.
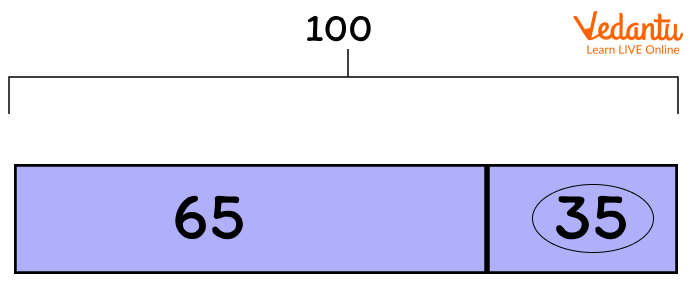
The bar model does not provide an answer but gives a clear understanding of what calculation is required to find an answer. For example, in the above problem, 35 is the answer as 65 and 100 are already given and we can solve this by taking 65 out of 100.
Conclusion
In short, the bar model is a pictorial representation of problems or concepts where bars or rectangular boxes are used to represent the known and unknown quantities. Bar models are used to solve numerical problems with four arithmetic operations namely addition, subtraction, multiplication, and division. In word problems, bar models help students to decide which Mathematical operation should be used to visualise problems.
FAQs on Bar Model in Maths: What It Is, How It Works & Examples
1. What exactly is a bar model in Maths?
A bar model is a visual problem-solving strategy used in mathematics. It involves drawing rectangular bars to represent numbers and quantities in a problem. This method helps students visualise the relationship between known and unknown values, making it easier to understand which operation (like addition, subtraction, multiplication, or division) is needed to find the solution.
2. How does a bar model work to solve a Math problem?
A bar model works by breaking down a math problem into a simple diagram. You draw a bar to represent the 'whole' amount and divide it into smaller bars to represent the 'parts'. For example, in a word problem, you would identify the known numbers and the unknown number you need to find. By placing the known values into the bars, the diagram makes it visually clear what the unknown value is and how to calculate it.
3. What are the key benefits of using the bar model method?
The key benefits of using the bar model method include:
It provides a visual representation of abstract problems, which is helpful for all learners.
It helps in understanding complex word problems by simplifying them into parts.
It builds a strong foundation for understanding various mathematical concepts like fractions, percentages, and ratios.
It is a versatile strategy that can be applied to a wide range of topics, from basic arithmetic to more complex algebra.
4. How do you use a bar model for a subtraction word problem?
To solve a subtraction problem using a bar model, you start by drawing a long bar to represent the total amount (the 'whole'). Then, you draw a smaller bar below it to represent the part that is known or being taken away. The remaining empty space in the top bar visually represents the unknown quantity you need to find. For example, if 'Ria had 10 apples and gave 4 to Sam', the top bar represents 10, a part of it represents 4, and the remaining part is the answer.
5. What is the difference between a bar model and a bar graph?
The primary difference is their purpose. A bar model is a mathematical tool used to solve problems by visualising the relationship between numbers. In contrast, a bar graph is a statistical tool used to represent and compare data. A bar model helps you calculate an answer, while a bar graph helps you see the distribution or comparison of a set of collected information.
6. Can bar models be used for more advanced topics like fractions and percentages?
Yes, bar models are extremely effective for teaching fractions and percentages. For fractions, a single bar can represent a whole, which is then divided into equal parts to show fractions like 1/2 or 3/4. For percentages, the entire bar represents 100%, and different segments of the bar can represent various percentages, making it easier to calculate and understand concepts like '25% of 80'.
7. Why is it important that the bars in a bar model are proportional?
It's important for the bars to be proportional because it helps students develop a sense of number magnitude and relationship. A larger bar visually represents a larger number, and a smaller bar represents a smaller number. This proportional drawing helps to make the mathematical relationship intuitive. For example, in a comparison problem, seeing one bar clearly longer than another reinforces the concept of 'greater than' or 'less than' before any calculation is even performed.























