Concise Mathematics Class 10 ICSE Solutions for Chapter 19 - Constructions (Circles)

Exercise – 19

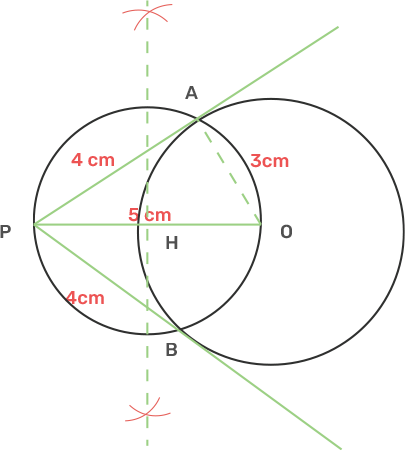
1. Draw a circle of radius 3 cm. Mark a point P at a distance 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.

Ans: Draw a circle with centre O and Radius 3 cm.

From point O take another point P as the distance between O and P is 5 cm.

Draw a bisector of OP that cuts the OP at M.

Take centre M and Radius OM, draw another circle which intersects the given circle at A and B.

Join AP and BP.

AP and BP are the tangents.

In right angle triangle AOP:

${{H}^{2\text{ }}}=\text{ }{{\text{P}}^{2}}\text{ + }{{\text{B}}^{2}}$

$\Rightarrow \text{ O}{{\text{P}}^{2\text{ }}}=\text{ P}{{\text{A}}^{2\text{ }}}+\text{ O}{{\text{A}}^{2\text{ }}}----(1)$

We know that OP = 5cm, OA = 3cm

$\Rightarrow \text{ }{{\text{5}}^{2}}\text{ = P}{{\text{A}}^{2}}\text{ + }{{\text{3}}^{2}}$

$\Rightarrow \text{ P}{{\text{A}}^{2\text{ }}}=\text{ 25 - 9}$

$\Rightarrow \text{ PA = 4}$

So PA = 4 cm

Similarly we get BP = 4 cm

The length of AP and BP after measurement is 4 cm.

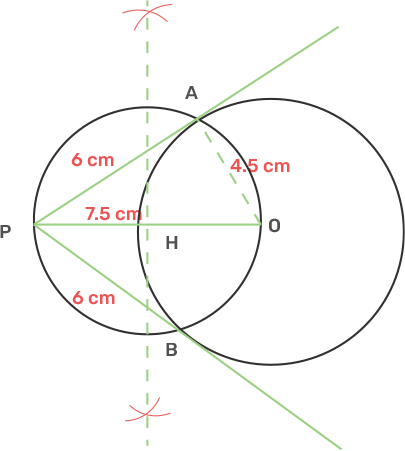
2. Draw a circle of diameter 9 cm. Mark a point at a distance 7.5 cm from the centre of the circle drawn. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.

Ans: Radius of the given circle is half the diameter.

Draw a circle with centre O and Radius 4.5 cm.

From point O take another point P as the distance between O and P is 7.5 cm.

Draw a bisector of OP that cuts the OP at M.

Take centre M and Radius OM, draw another circle which intersects the given circle at A and B.

Join AP and BP.

AP and BP are the tangents.

In right angle triangle AOP :

${{H}^{2\text{ }}}=\ {{P}^{2\text{ }}}+\text{ }{{\text{B}}^{2}}$

$\Rightarrow \text{ O}{{\text{P}}^{2}}\text{ = P}{{\text{A}}^{2\text{ }}}+\text{ O}{{\text{A}}^{2}}\text{ ---- (1)}$

We know that OP = 7.5 cm, OA = 4.5 cm

$\Rightarrow \text{ 7}\text{.}{{\text{5}}^{2\text{ }}}=\ P{{A}^{2\text{ }}}+\text{ 4}\text{.}{{\text{5}}^{2}}$

$\Rightarrow \text{ P}{{\text{A}}^{2\text{ }}}=\text{ 56}\text{.25 - 20}\text{.25 }$

$\Rightarrow \text{ P}{{\text{A}}^{2}}\text{ = 36}$

$\Rightarrow $ PA = 6

So PA = 6 cm

Similarly we get BP = 6 cm

The length of AP and BP after measurement is 6 cm.

3. Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between tangents is 45°.

Ans: Draw a circle with centre O and Radius 5 cm.

Draw an arc making an angle 135° as 180° - 45° = 135° and mark angle AOB.

From point A and B draw two rays making an angle of 90° at each point which meet each other at point P, outside the circles.

Join AP and BP.

AP and BP are the tangents that make an angle 45° with each other at P.

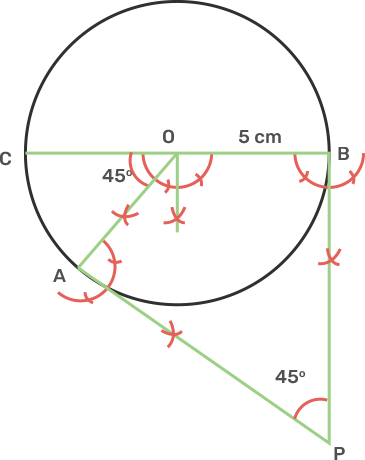
{Please add the dimensions in diagram: OB = 5 cm}

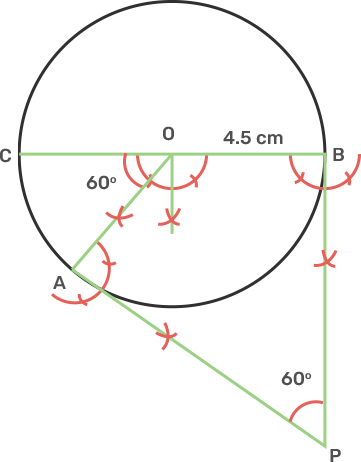
4. Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between tangents is 60°.

Ans: Draw a circle with centre O and Radius 4.5 cm.

Draw an arc making an angle 120° as 180° - 60° = 120° and mark angle AOB.

From point A and B draw two rays making an angle of 90° at each point which meet each other at point P, outside the circles.

Join AP and BP.

AP and BP are the tangents that make an angle 60° with each other at P.

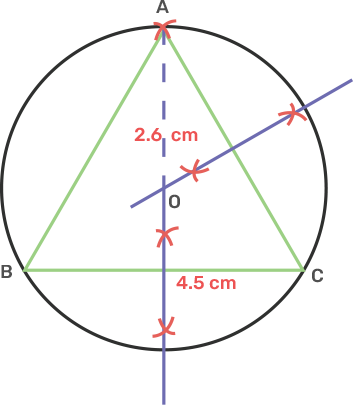
5. Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.

Ans: Draw a line segment BC as 4.5 cm.

Take centre B and C draw two arcs of radius 4.5 cm which intersect each other at A.

Join AC and AB.

Draw a perpendicular bisector of AC and BC intersecting each other at O.

Take centre O and radius OA, OB or OC draw a circle which passes through A, B and C.

The circle is circumscribed with triangle ABC.

The radius is measured as OA of 2.6 cm.

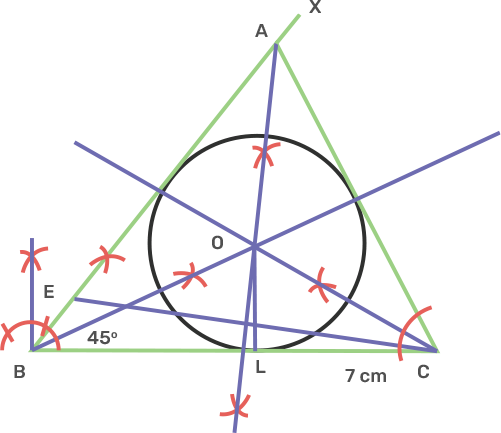
6. Using ruler and compasses only.

i) Construct triangle ABC, having given BC = 7 cm, AB - AC = 1 cm and angle ABC = 45°.

Ans: i) Triangle Construction:

Draw a line segment BC as 7 cm.

Take centre B, draw a ray BX making an angle of 45° and cut off BE as 1 cm.

Join EC and draw the perpendicular bisector of EC intersecting BX at A.

Join AC.

The triangle obtained is ABC.

ii) Inscribe a circle in the triangle ABC constructed in (i) above.

Ans: Incircle Construction:

Draw a bisector of angle ABC and ACB intersecting each other at O.

Take a point O and draw perpendiculars OL to BC.

Again take O as a centre and OL as radius draw a circle which touches the side of triangle ABC.

This is required incircle of triangle ABC.

After measurement radius OL is 1.8 cm.

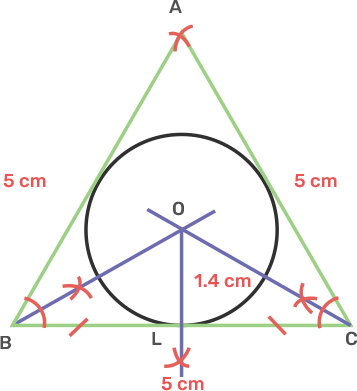
7. Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.

Ans: Draw a line segment BC as 5 cm.

Take centre B and C draw two arcs of 5 cm radius each which intersect each other at A.

Join AB and AC,

Draw angle bisector of angle B and C intersecting each other at O.

From O, draw OL perpendicular to BC.

Take centre O and radius OL, draw a circle that touches the triangle ABC.

After measurement radius OL is 1.4 cm.

8. Using ruler and compasses only,

i) Construct a triangle ABC with following data:

Base AB = 6 cm, BC = 6.2 cm and angle CAB = 60°.

Ans: i) Draw a line segment AB as 6 cm.

Take point A and make an angle 60° with BC.

Take B as centre and radius 6.2 cm and draw an intersecting arc on AX at C.

Join BC.

The obtained figure is the triangle of ABC.

ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre O.

Ans: Draw a perpendicular bisector of  BC and AC intersecting each other at O.

Take centre O and radius OA, OB or OC, draw a circle which passes through A, B, C.

iii) Draw a perpendicular from O to AB which meets AB in D.

Ans: Take point O and draw perpendicular to AB meets at D.

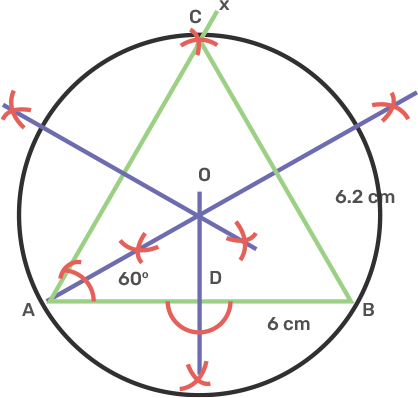
iv) Prove that: AD = BD.

Ans: In the right angle triangle OAD and OBD.

The radius of circle OA is equal to OB.

The side OD is common.

The angle D is perpendicular.

From RHS the triangle OAD and OBD is congruent.

Therefore, by CPCT,

AD = BD

9. Using ruler and compasses only construct a triangle ABC in which BC = 4cm, angle ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.

Ans: Draw a line segment BC as 4 cm.

Take point C and draw a perpendicular line CX and form it, cut off CE is 2.5 cm.

From E draw a perpendicular line EY.

From C draw a ray making an angle 45° with CB, which intersect EY at A.

Join AB.

The obtained figure is the triangle of ABC.

Draw a perpendicular bisector of sides AB and BC intersecting each other at O.

Take O as centre, join OB and take it as radius, draw a circle which passes through A, B, C.

After measurement the radius is 2 cm.

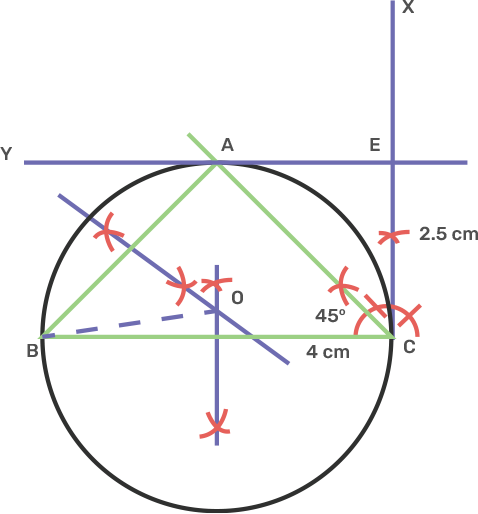
10. Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.

i) What do you call the point O?

Ans: 

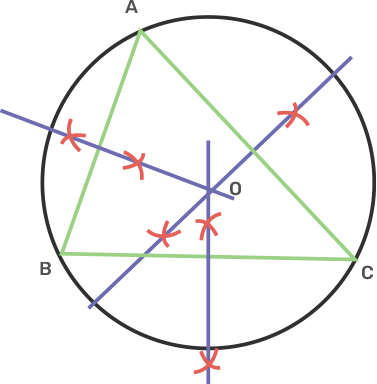
i) The point O is called the circumcentre of the circumcircle of triangle ABC.

ii) What is the relation between the distances OA, OB and OC?

Ans: The side OA, OB, OC are the radii of the circumcircle.

iii) Does the perpendicular bisector of BC pass through O?

Ans: The perpendicular bisector of BC will pass through O.

11. The bisector of angles A and B of a scalene triangle ABC meet at O.

i) What is the point O called?

Ans: 

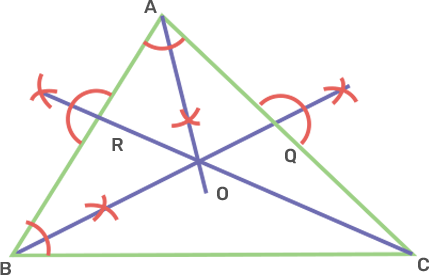
i) The point O is called the incentre of incircle of the triangle ABC. 

ii) OR and OQ are perpendiculars drawn to AB and AC respectively. What is the relation between OR and OQ?

Ans: The side OR and OQ are the radii of the incircle and are equal to each other.

iii) What is the relation between angle ACO and angle BCO?

Ans: OC is the bisector of angle C. Therefore, angle ACO and BCO are equal.

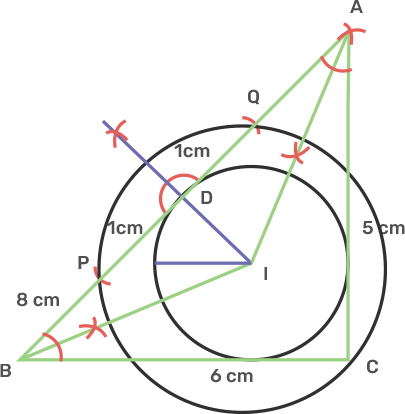
12. i) Using ruler and compasses only, construct a triangle ABC in which AB = 8cm, BC = 6 cm and AC = 5 cm.

Ans: Draw a line segment BC as 6 cm.

Take centre B and radius 8 cm, draw an arc.

Again Take centre C and radius 5 cm, draw another arc that intersect the first arc at A.

Join AB and AC.

The triangle ABC obtained.

ii) Find its incentre and mark it I.

Ans: Now draw the angle bisector of the B and A intersecting each other at I.

The I is called the incentre of the triangle.

iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.

Ans: Again from this point I, draw ID perpendicular to AB.

Now from D cut off DP and DQ as 1 cm.

Take centre I, and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.

13. Construct an equilateral triangle ABC with sides 6cm. Draw a circle circumscribing the triangle ABC.

Ans: Draw a line segment BC as 6 cm.

Take centre B and C and radius 6 cm, draw an arc intersecting each other at point A.

Join AB and AC.

Draw perpendicular bisectors of AC, AB and BC intersecting each other at O.

Take centre O and radius OA or OB or OC, draw a circle which passes through A, B and C.

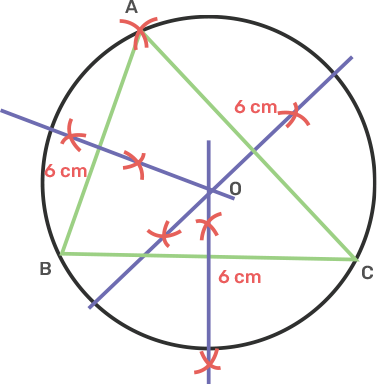
The circle obtained is the circumcircle of the equilateral triangle ABC.

14. Construct a circle, inscribing an equilateral triangle with side 5.6 cm.

Ans: Draw a line segment BC as 5.6 cm.

Take centre B and C and radius 5.6 cm, draw two arc intersecting each other at point A.

Join AB and AC

Draw angle bisectors of B and C intersecting each other at O. 

Take centre O draw OL perpendicular to BC.

Now take centre O and radius OL, draw a circle which will touch the sides of triangle ABC.

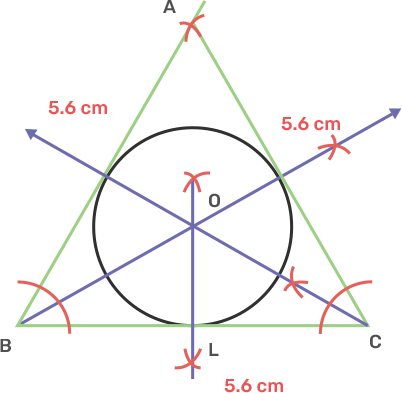
The circle obtained is inscribed the equilateral triangle ABC.

15. Draw a circle circumscribing a regular hexagon with sides 5 cm.

Ans: The interior angle of a regular hexagon is 120°.

Draw a regular hexagon ABCDEF that each side equal to 5 cm and each interior angle 120°.

Join its diagonal AD, BE, and CF intersecting each other at O.

Take centre O and radius OA, draw a circle which will pass through the vertices A, B, C, D, E and F.

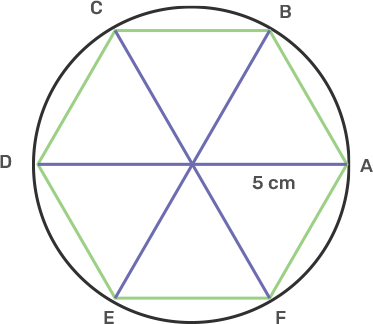
The circle is the circumcircle of a regular hexagon.

16. Draw an inscribing circle of a regular hexagon of side 5.8 cm.

Ans: The interior angle of a regular hexagon is 120°.

Draw a line segment AB as 5.8 cm.

Take point A and B, draw rays making an angle of 120° each cut off AF and BC as 5.8 em.

Take point F and C, draw rays making an angle of 120° each cut off FE and CD as 5.8 cm.

Join its DE, and CF intersecting each other at O.

From O draw a perpendicular OL to AB.

Take centre O and radius OL, draw a circle which touches the sides of the hexagon.

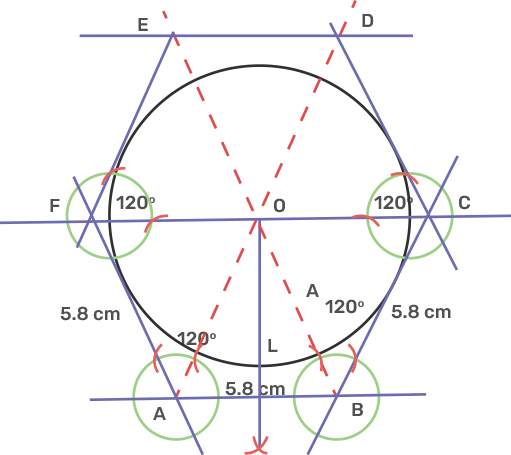
The circle is the incircle of a regular hexagon.

17. Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.

Ans: Draw a circle of radius 4 cm and centre as O.

Now draw radii OA and OB such that angle AOB is 60°.

Cut off arc BC, CD, EF and each arc equal to arc AB on the given circle.

Join its AB, BC, CD, DE, EF and FA to get a regular hexagon.

The circle is the circumcircle of a regular hexagon.

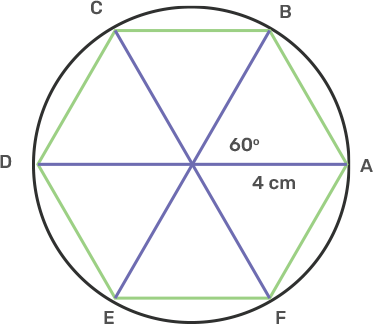
18. Draw a circle of radius 3.5 cm. Mark the point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.

Ans: Draw a line segment OP is 6 cm.

Take centre O and radius 3.5 cm, draw a circle .

Draw the midpoint of OP.

Take centre M and diameter OP, draw a circle which intersect the circle at T and S.

Join PT and PS.

PT and PS are the tangents.

The length of PT and PS after measurement was found as 4.8 cm.

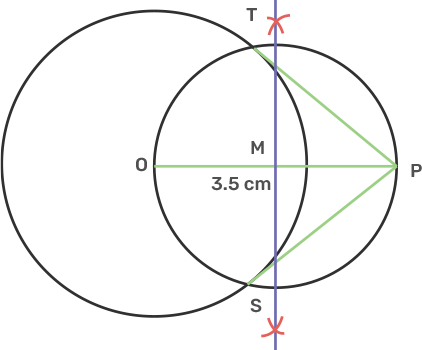
19. Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm angle ABC = 120°

i) Construct a circle circumscribing the triangle ABC.

Ans: Draw a line segment BC is 5.5 cm.

Draw line AB as 6 cm such that angle ABC is 120°.

Join AC then we will get triangle ABC.

Draw the perpendicular bisectors of AB and BC and intersect at O.

Take centre O and radius OA and draw the circle.

ii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B to C.

Ans: Extend the perpendicular bisector of BC such that it intersects the circle at D.

Join BD and CD,

Here, BD is equal to DC.

Join D with point A then will get cyclic quadrilateral ABCD.

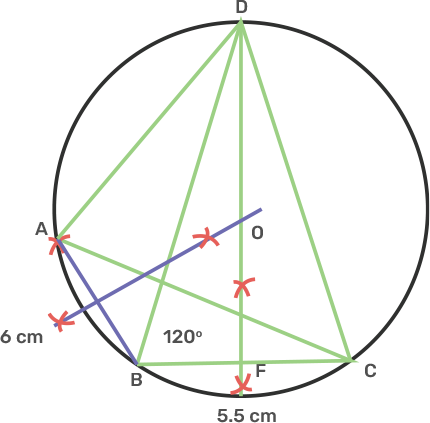
20. Using a ruler and compasses only:

i) Construct a $\Delta BMP$ with the following data:

AB = 3.5 cm, BC = 6 cm and angle ABC = 120°

Ans: Draw a line segment BC is 6 cm.

Take point B, draw a ray BX making an angle of 120° with BC with B as centre and radius 3.5 cm, cut off AB is 3.5 cm and join AC.

Thus, ABC is the obtained triangle.

ii) In the same diagram, draw a circle with BC as diameter. Find a point P on circumference of the circle which is equidistant from AB and BC.

Ans: Draw the perpendicular bisector of MN of BC which cuts BC at point O.

Take radius as OB and centre as O and draw a circle.

Draw angle bisector of ABC which meets circle at point P and point P is equidistant from AB and BC.

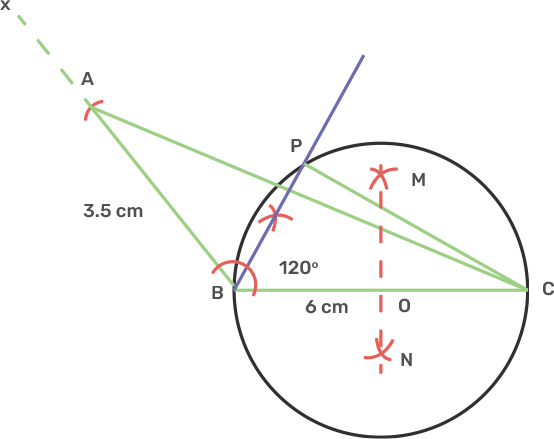
iii) Measure angle BCP.

Ans: We know that angle subtended on diameter from a point on circumference is 90°.

So Angle BPC = 90°.

BP is angle bisector of angle B, So angle CBP = 60°

Therefore the angle BCP is 30°.

21. Construct a $\Delta ABC$ with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.

Ans: Draw a line segment BC is 6.5 cm.

Take point B as centre, draw an arc of radius 5.5 cm.

Take point C as centre, draw an arc of radius 5 cm.

Both the arc intersects at A.

Join AB and AC.

Thus, ABC is the obtained triangle.

Draw the angle bisector of angle ABC and ACB.

The bisector meets each other at O.

Draw ON perpendicular to BC.

Take O as centre and radius ON, draw an incircle that touches all sides of triangle ABC.

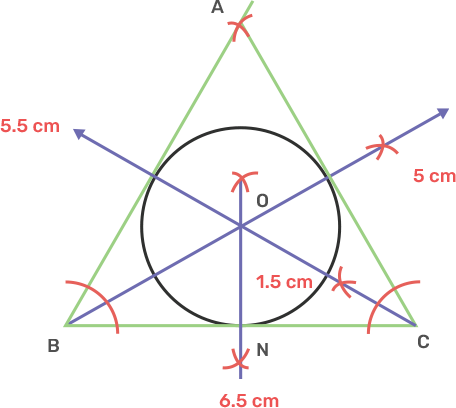
The length of radius ON is 1.5 cm.

22. Construct a $\Delta ABC$ with AB = 5.5 cm, AC = 6 cm and angle BAC = 105° Hence: 

i) Construct the locus of points equidistant from BA and BC.

Ans: Draw a line segment AB is 5.5 cm.

Draw angle BAR as 105°.

Take centre A and radius 6 cm cut off an arc AR at C.

Join BC, ABC is the triangle.

Draw the angle bisector BD of angle ABC the locus of point equidistant from BA and BC.

ii) Construct the locus of points equidistant from B and C.

Ans: Draw the perpendicular bisector EF of BC, gives the locus of point equidistant from B and C.

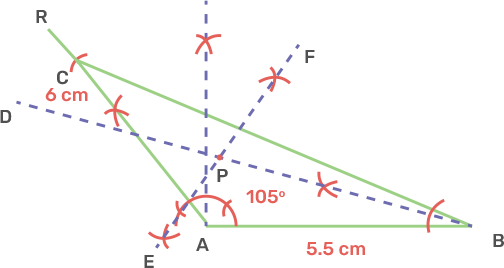
iii) Mark the point which satisfies the above two loci as P. Measure and write the length of the PC.

Ans: BD and EF intersect each other at point P.

Thus, P satisfies the above two loci.

The length of the PC is 4.8 cm.

23. Draw a regular hexagon of 5 cm.

Ans: Draw a line segment AF as 5 cm.

Take point A as centre and radius equal to AF, draw an arc above AF.

Take point F as centre and same radius equal to AF, cut the previous arc Z.

Take point Z as centre and the same radius equal to AF, draw a circle passing through A and F.

Take point A as centre and the same radius equal to AF, cut the circle above AF at B.

Take point B as centre and the same radius equal to AF, cut the circle at C.

Repeat the process to get remaining vertices of the hexagon at D.

Join consecutive arcs on the circle to form the hexagon.

Draw the perpendicular bisector of AF, EF and DE.

Extend the bisector of AF, FE, DE to meet CD, BC, AB at X, L, O respectively.

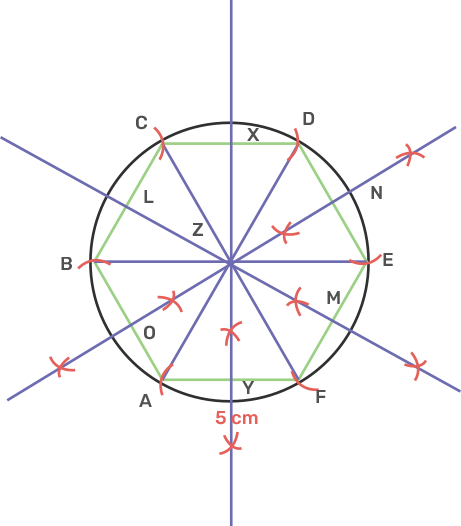
Join AD, CF, and EB.

24. Draw a line AB = 5cm. Mark a point C on AB such that AC = 3 cm. Using ruler and a compass only, construct:

i) a circle of radius 2.5 cm, passing through A and C.

Ans: Draw a line segment AB as 5 cm.

Take point A as centre and cut an arc of 3 cm on AB to obtain C.

Take point A as centre and cut an arc of 2.5 cm above AB.

Take the same radius and C as centre, draw another arc that cuts the previous arc and mark the intersection point as O.

Take centre as O and radius 2.5 cm, draw a circle so that points A and C lie on the circle formed.

Join OB.

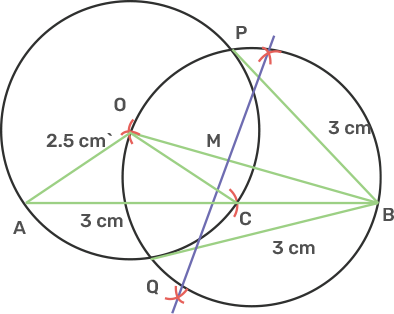
ii) construct two tangents to the circle from the external point B. Measure and record the length of the tangents.

Ans: Draw the perpendicular bisector of OB to obtain the midpoint of OB as M.

Take M as a centre and radius equal to OM, draw a circle to cut the previous circles at points P and Q.

Join PB and QB, PB and QB are the tangent to the given circle from exterior point B.

QB and PB is 3 cm.

The length of the tangent is 3 cm.

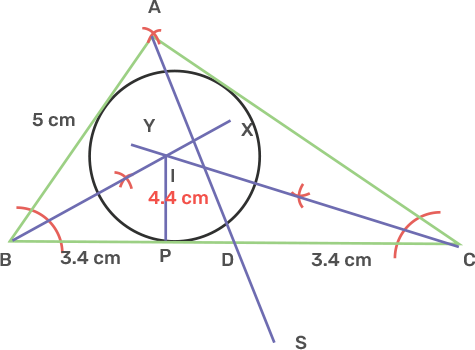
25. Using a ruler and a compass, construct a triangle ABC in which AB = 7cm, angle CAB = 60° and AC = 5 cm. Construct the locus of:

i) point equidistant from AB and AC.

Hence construct a circle touching the three sides of the triangle internally.

Ans: i) Draw a line segment AB as 7 cm.

Take point A as centre and draw an arc of circle which intersects AB at M.

Take point M as centre and the same radius as before drew an arc intersecting previously drawn arc at point N.

Draw the ray AX that is passing through N and the angle XAB is 60°.

Taking A as centre and radius equal to 5 cm, draw an arc cutting AX at C.

Join BC.

The triangle ABC is obtained.

ii) point equidistant from BA and BC.

Ans: Draw the angle bisector of angle CAB and ABC and mark the intersecting point as O.

Take the centre as O, draw a circle with radius OD.

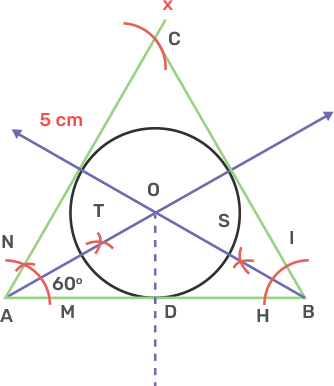
26. Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.

Ans: Draw a line segment BC as 6.8 cm.

Mark a point D as BD is equal to DC is 3.4 cm that is the midpoint of BC.

Mark another point A that intersects the arc AD (4.4 cm) and AB (5 cm) from point D and B respectively.

Join AB, AC and AD.

The triangle ABC is obtained.

Draw the angle bisector of angle B and C which are rays BX and CY and I is the incentre of a circle.

From I draw a perpendicular on BC as IP.

Take centre as I and radius as IP and draw the circle of radius IP and that is incircle of triangle ABC.

27. Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both tangents, show that they are equal to each other.

Ans: Draw a concentric circle of radius 4 cm and 6 cm with centre O.

Mark point P on the outer circle.

Join OP,

Draw a perpendicular bisector of OP where M is the midpoint of OP.

Take a distance of point O from M and mark arcs from M on the inner circle it cuts a point A and B respectively.

Join PA, PB.

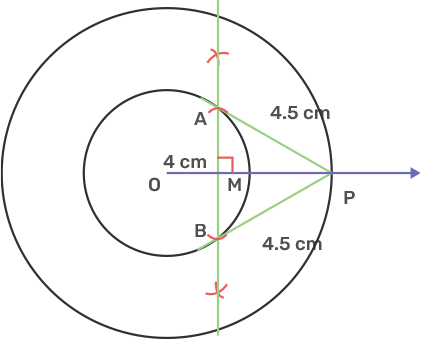
From diagram we can see that:

$\Rightarrow \text{ AM = BM}$ 

$\Rightarrow \text{ PM = PM}$

angle AMP = angle BMP = 90°

So $\Delta AMP$ and $\Delta BMP$ are similar triangles. So by CPCT we can say AP = BP.

It is observed from the Figure that PA and PB are the tangents from the outer circle to inner circle are equal in length 4.5 cm each.

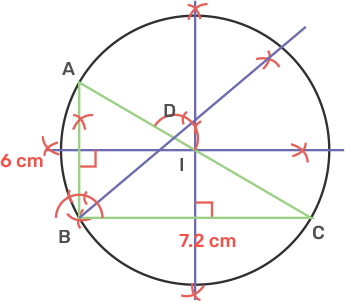
28. In triangle ABC, angle = 90°, side AB = 6 cm, side BC = 7.2 cm and BD is perpendicular to side AC. Draw a circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.

Ans: Draw a line segment BC of length 7.2 cm.

Draw an angle ABC 90° using a compass.

Draw BD perpendicular to AC using a compass.

Join BD.

Draw a perpendicular bisector of AB and BC that intersect at I, where I is the circumcenter of a triangle.

Draw a circumcircle by using circumcenter I and IC as the radius and the radius of the circle obtained is 4.7cm.

Steps to Prepare for Class 10 ICSE Exams

Students in grade 10 are in a crucial state, their board exams are in the near future. They should do as much practice as possible. It is because their board exams decide which career to choose. Their board marks are important to get a strong career. It is just the foundation that is built by the students by securing marks. To secure good marks, students must start their preparation right away. Students must be in the revision phase by this time. The first time for preparation will be knowing the syllabus. The Vedantu website provides you with an updated syllabus that follows ICSE standards. 

The second step will be going through the important questions. Students need to learn the important questions because the important questions tell you how to approach a question. It also gives you all the possibilities of twisted questions that can be asked in the main exam. This helps them beware of every question possible. Also, it tells you the importance and weightage of every concept. It keeps changing year over year. So it is necessary to check the updated syllabus and update important questions.

The final step in the preparation would be taking up a mock test. The more and more practice you do, the better your scores will be. Make sure to practice the mock test twice a week. It gives an overview of how the exam works and how its environment will be. So taking up mock tests will give them enough confidence to face the examination. And the best part of this whole preparation is, 1) it gives you an incredible output. An amazing score and 2) all these materials are available for free on the Vedantu website right from the updated syllabus to the important questions to the mock test PDFs. Make use of them! Grab the opportunity.  

What can I do If I have Doubts?

Doubt clarification is another important parameter in your preparation. It has to be sorted now and then to have a clear understanding of the concept. Or else the concepts following it will be chaotic. To avoid this situation, students can either post their doubts on the Vedantu website or can register for online doubt clarification sessions. Either way is to make sure that students are free from doubts. The doubts are clarified by our own team and subject experts who have extensive work experience in teaching the same subject. Do your preparation well and Good Luck with your examination.

Conclusion

Preparing for Class 10 ICSE Concise Mathematics for chapter 19 is quite helpful with the assistance of online PDF file