Concise Mathematics Class 10 ICSE Solutions for Chapter 15 - Similarity (With Applications to Maps and Models)

Exercise 15(A)

1. In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:

(i) ΔAPC and ΔBPD are similar.

(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.

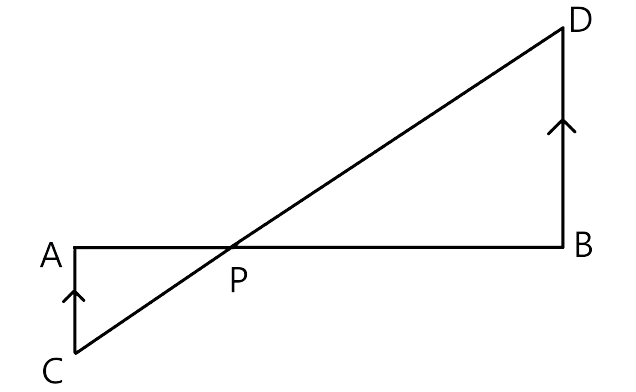
Ans:  At point P, two line segments AB and CD intersect each other. AC || BD and we have to prove that 

(i) ΔAPC ~ ΔBPD

(ii) If BD = 2.4cm, AC = 3.6cm, PD = 4.0 cm and PB = 3.2, find length of PA and PC

Proves 

(i) In ΔAPC and ΔAPD

\[\angle APC{\text{ }} = \angle BPD{\text{ }}\left( {Vertically{\text{ }}opp.{\text{ }}angles} \right)\]

∠PAC = ∠PBD (Alternate angles)

ΔAPC ~ ΔBPD (AA axiom)

(ii) From the figure we can say that the corresponding parts of the similar triangle are equal, then we have 

$\dfrac{{PA}}{{PB}} = \dfrac{{PC}}{{PD}} = \dfrac{{AC}}{{BD}}$

In the questions its given that BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm

On substituting the values, we have 

$\dfrac{{PA}}{{3.2}} = \dfrac{{PC}}{4} = \dfrac{{3.6}}{{2.4}}$

$\dfrac{{PA}}{{3.2}} = \dfrac{{3.6}}{{2.4}}$and$\dfrac{{Area{\text{ of }}\Delta {\text{BPQ}}}}{{Area{\text{ of }}\Delta {\text{CPD}}}} = \dfrac{{(B{P^2})}}{{(C{P^2})}} = \dfrac{1}{4}$

Thus, 

$\dfrac{{PA}}{{3.2}} = \dfrac{{3.6}}{{2.4}}{\text{ and }}\dfrac{{PC}}{4} = \dfrac{{3.6}}{{2.4}}$

Furthermore we can say that 

PA = (3.6 x 3.2)/ 2.4 = 4.8 cm and

PC = (3.6 x 4)/ 2.4 = 6 cm

2. In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:

(i) ΔAPB is similar to ΔCPD.

(ii) PA × PD = PB × PC.

Ans: 

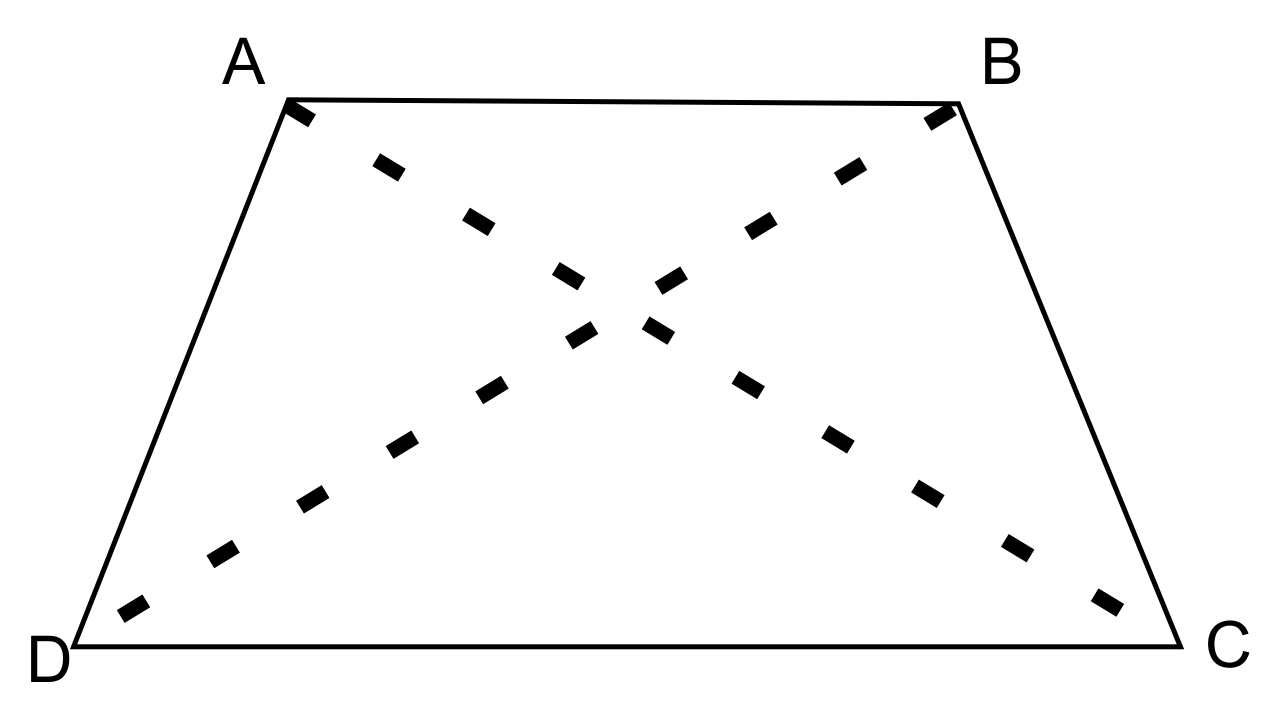
To prove that, 

(i) ΔAPB is similar to ΔCPD.

In ∆APB and ∆CPD, we have 

∠APB = ∠CPD as they are vertically opposite angles 

∠ABP = ∠CDP, Alternate angles as, AB||DC

Thus, ∆APB ~ ∆CPD is as per the AA similarity criterion. 

(ii) To prove that, PA × PD = PB × PC.

As we know that As ∆APB ~ ∆CPD

And since the corresponding sides of similar triangles are proportional, we have

$\dfrac{{PA}}{{PC}} = \dfrac{{PB}}{{PD}}$

Thus after cross multiplying, we have,

PA × PD = PB × PC

3. P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:

(i) DP : PL = DC : BL.

(ii) DL : DP = AL : DC.

Ans:  

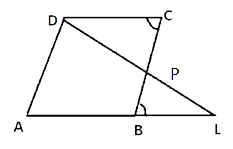
To prove that 

(i) DP: PL = DC: BL. 

As AD||BC, we can also have AD|| BP also 

So, from BPL

$\dfrac{{DP}}{{PL}} = \dfrac{{AB}}{{BL}}$

And, since ABCD is a parallelogram, AB = DC

Hence,

$\dfrac{{DP}}{{PL}} = \dfrac{{DC}}{{BL}}$

And since it’s known that ABCD is a parallelogram, AB = DC

Therefore, $\dfrac{{DP}}{{PL}} = \dfrac{{DC}}{{BL}}$

Which is nothing but DP: PL = DC: BL. 

(ii) DL: DP = AL: DC

As it has been mentioned that AD||BC, we also can say that AD|| BP

From BPL, we have 

$\dfrac{{DL}}{{DP}} = \dfrac{{AL}}{{AB}}$

$\dfrac{{DL}}{{DP}} = \dfrac{{AL}}{{AB}}$

As ABCD is a parallelogram, we can say that AB = DC

Therefore,$\dfrac{{DL}}{{DP}} = \dfrac{{AL}}{{AB}}$

Which is nothing but DL: DP = AL: DC

4. In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that:

(i) ΔAOB is similar to ΔCOD.

(ii) OA x OD = OB x OC.

Ans:  

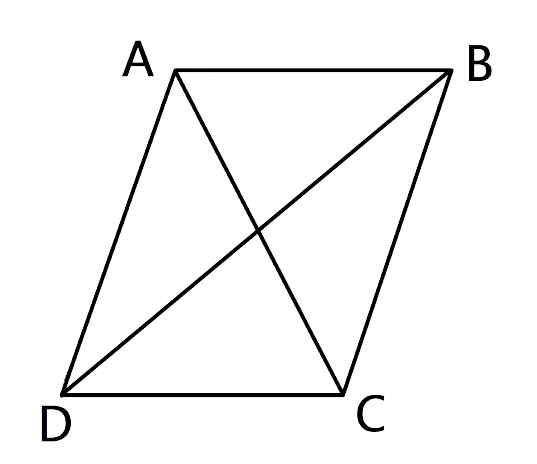
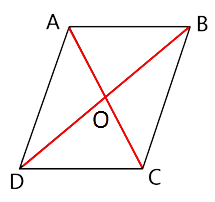
(i) ΔAOB is similar to ΔCOD

Given in the question that 

AO = 2CO and BO = 2DO,

$\dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}} = \dfrac{2}{1}$

From the vertically opposite angles property, we can say that ∠AOB = ∠DOC 

Hence by SAS criterion for similarity, we can say that ΔAOB is similar to ΔCOD

(ii) OA × OD = OB × OC.

As we know that $\dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}} = \dfrac{2}{1}$

Thus from the given information, we can say that OA × OD = OB × OC

5. In ΔABC, angle ABC is equal to twice the angle ACB, and the bisector of angle ABC meets the opposite side at point P. Show that:

(i) CB: BA = CP: PA

(ii) AB x BC = BP x CA

Ans: 

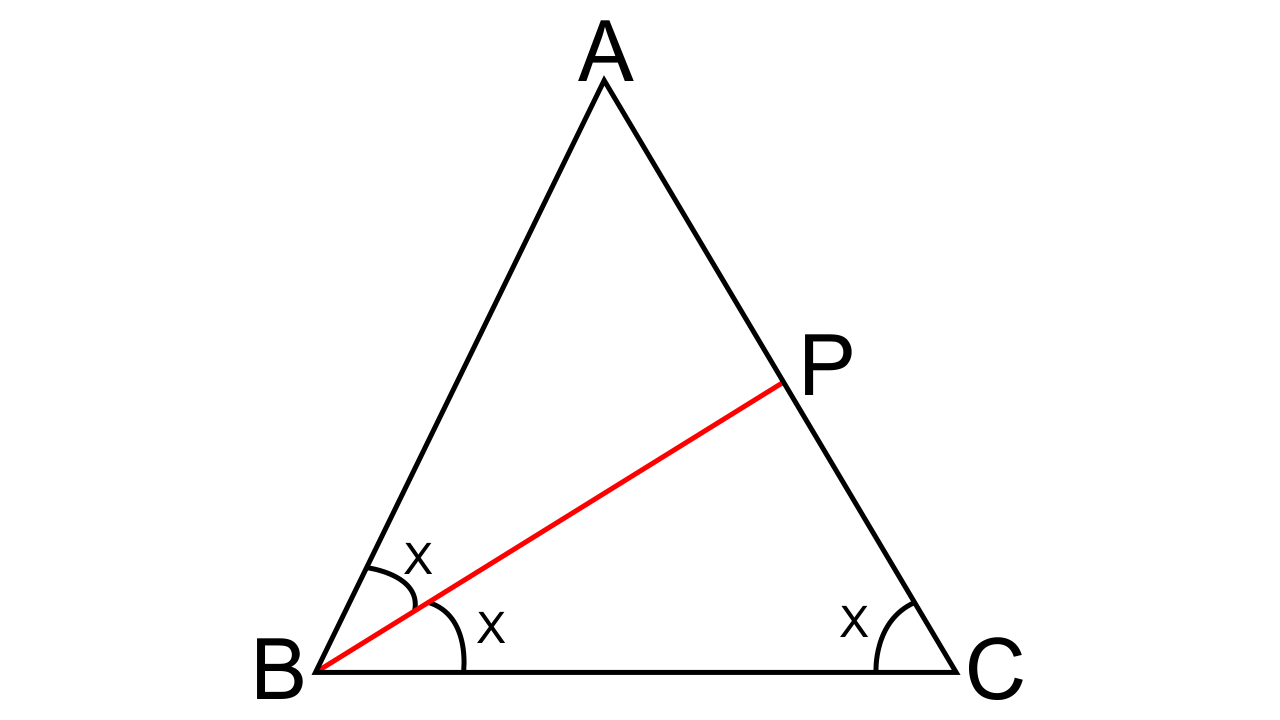
(i) As given, 

In Δ ABC, we have 

∠ABC = 2 ∠ACB

Now let us consider that ∠ACB = x

So, from this, we can also say that ∠ABC = 2x

Also, it is given that, BP is the bisector of ∠ABC

Hence, ∠ABP = ∠PBC = x

As we know from the angle bisector theorem, that the bisector of an angle divides the side opposite to it in the ratio of the other two sides.

Therefore, CB: BA = CP: PA.

(ii) To show that AB x BC = BP x CA

 In Δ ABC and Δ APB,

From exterior angle property, we can say that ∠ABC = ∠APB

∠BCP = ∠ABP

Thus by AA criterion for similarity, ∆ABC ~ ∆APB

In similar triangles, the corresponding sides are proportional ad from that we have

$\dfrac{{CA}}{{AB}} = \dfrac{{BC}}{{BP}}$

Therefore, AB × BC = BP × CA

6. In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:

$\mathbf{\dfrac{{AB}}{{AC}} = \dfrac{{BM}}{{CN}} = \dfrac{{AM}}{{AN}}}$

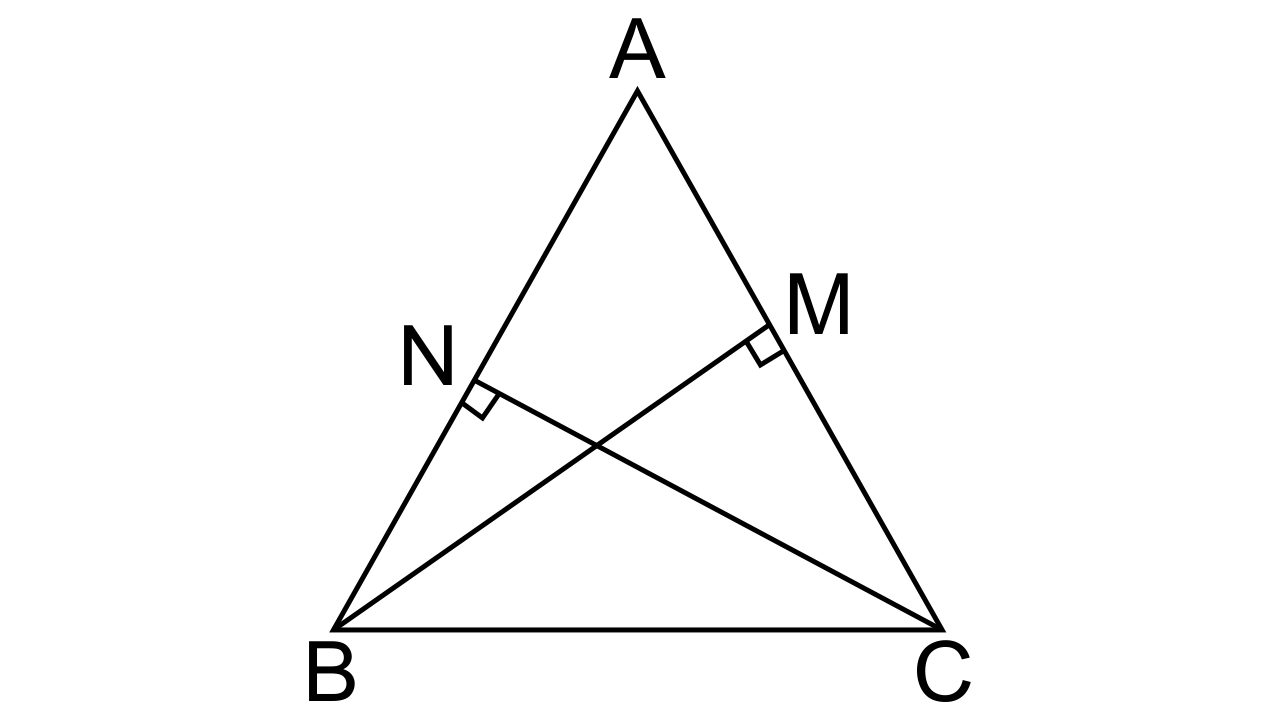
Ans: 

Let us consider two triangles, Δ ABM and Δ ACN. 

∠AMB = ∠ANC as BM ⊥ AC and CN ⊥ AB(given)

∠CAN=∠BAM(Common angle)

Hence by AA criterion for similarity, we can say that ∆ABM ~ ∆ACN

Furthermore by corresponding sides of similar triangles we have

$\dfrac{{AB}}{{AC}} = \dfrac{{BM}}{{CN}} = \dfrac{{AM}}{{AN}}$

7.In the given figure, DE // BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.

(i) Write all possible pairs of similar triangles.

(ii) Find lengths of ME and DM.

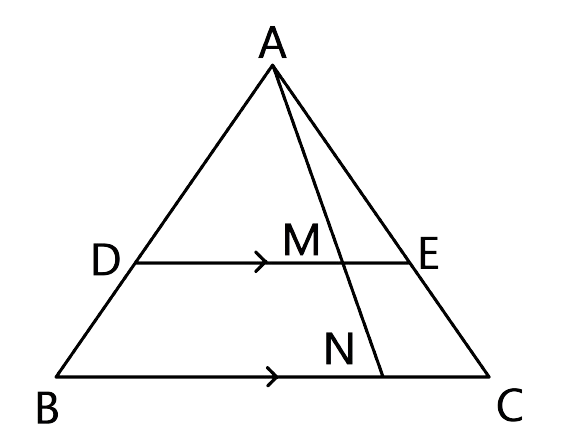
Ans: (i)In Δ AME and Δ ANC,

Since DE || BC so, ME || NC, we can say that ∠AME = ∠ANC

∠MAE = ∠NAC(common angle)

Hence, by AA criterion for similarity, we can say that ∆AME ~ ∆ANC.

Let us consider the Δ ADM and Δ ABN, 

Since DE || BC so, BC || BN, we can say that ∠ADM = ∠ABN

∠DAM = ∠BAN(common angle)

Hence, by the AA criterion for similarity, we can say that ∆ADM ~ ∆ABN

For Δ ADE and Δ ABC,

Since DE || BC so, ME || NC, we can say that, ∠ADE = ∠ABC

∠AED = ∠ACB as DE || BC

Hence, by the AA criterion for similarity, we can say that ∆ADE ~ ∆ABC

(ii) To find lengths of ME and DM.

Since we have proven that ∆AME ~ ∆ANC 

So, the corresponding sides of the similar triangle are proportional, we can say that 

$\dfrac{{AE}}{{AC}} = \dfrac{{ME}}{{NC}}$

$\dfrac{15}{24} = \dfrac{ME}{6}$

ME = 3.75 cm 

As we have proved above that ∆ADE ~ ∆ABC 

As the corresponding sides of a similar triangle are proportional, we have 

$\dfrac{{AE}}{{AC}} = \dfrac{{AD}}{{AB}} = \dfrac{{15}}{{24}}$ ……….. (1)

Also, ∆ADM ~ ∆ABN (As proven above)

As the corresponding sides of a similar triangle are proportional, we have 

$\dfrac{{AD}}{{AB}} = \dfrac{{DM}}{{BN}} = \dfrac{{15}}{{24}}$from equation(1)

$\dfrac{{DM}}{{24}} = \dfrac{{15}}{{24}}$

DM = 15 cm

8.In the given figure, AD = AE and AD² = BD x EC

Prove that: triangles ABD and CAE are similar.

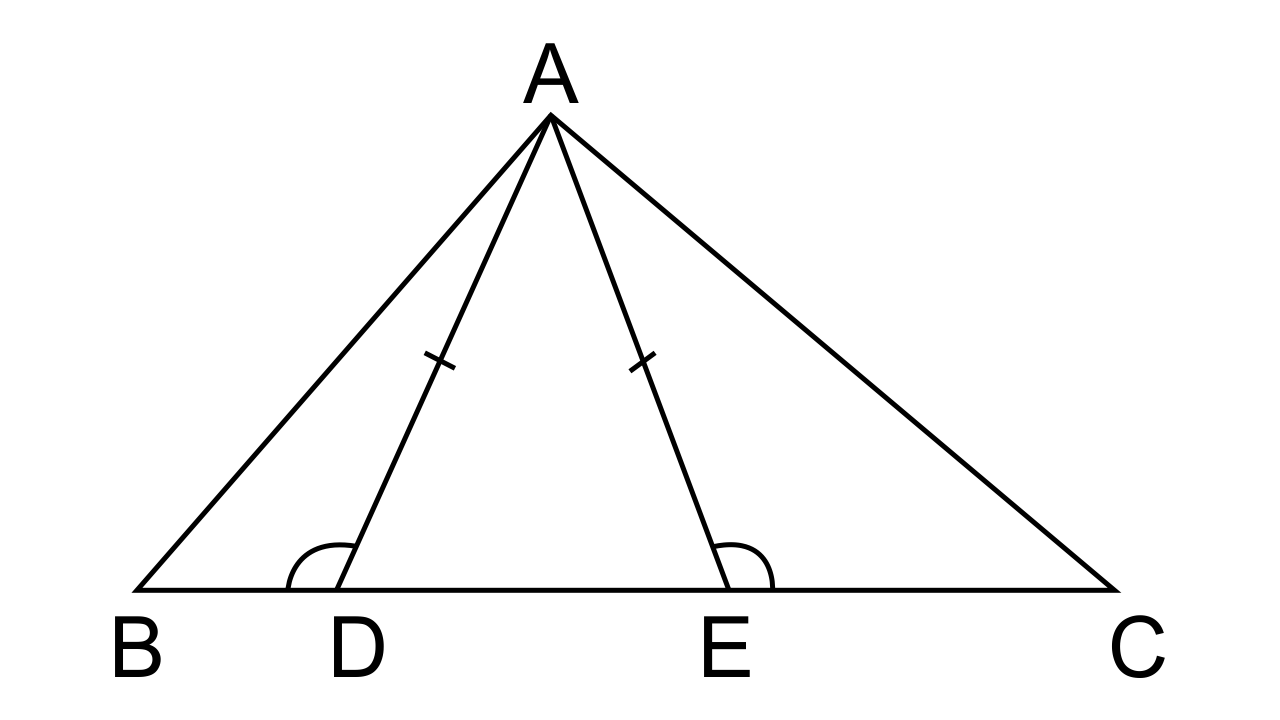
Ans: To prove that Δ ABD and Δ CAE are similar.

∠ADE = ∠AED (Angles opposite to equal sides are equal)

As ∠ADB + ∠ADE = 180° and ∠AEC + ∠AED = 180ׄ°, so we can say that ∠ADB = ∠AEC

And as its given that AD2 = BD × EC

$\dfrac{{AD}}{{BD}} = \dfrac{{EC}}{{AD}}$

$\dfrac{{AD}}{{BD}} = \dfrac{{EC}}{{AE}}$

By SAS criterion for similarity, we can say that ∆ABD ~ ∆CAE. 

9.In the given figure, AB // DC, BO = 6 cm and DQ = 8 cm; find: BP × DO

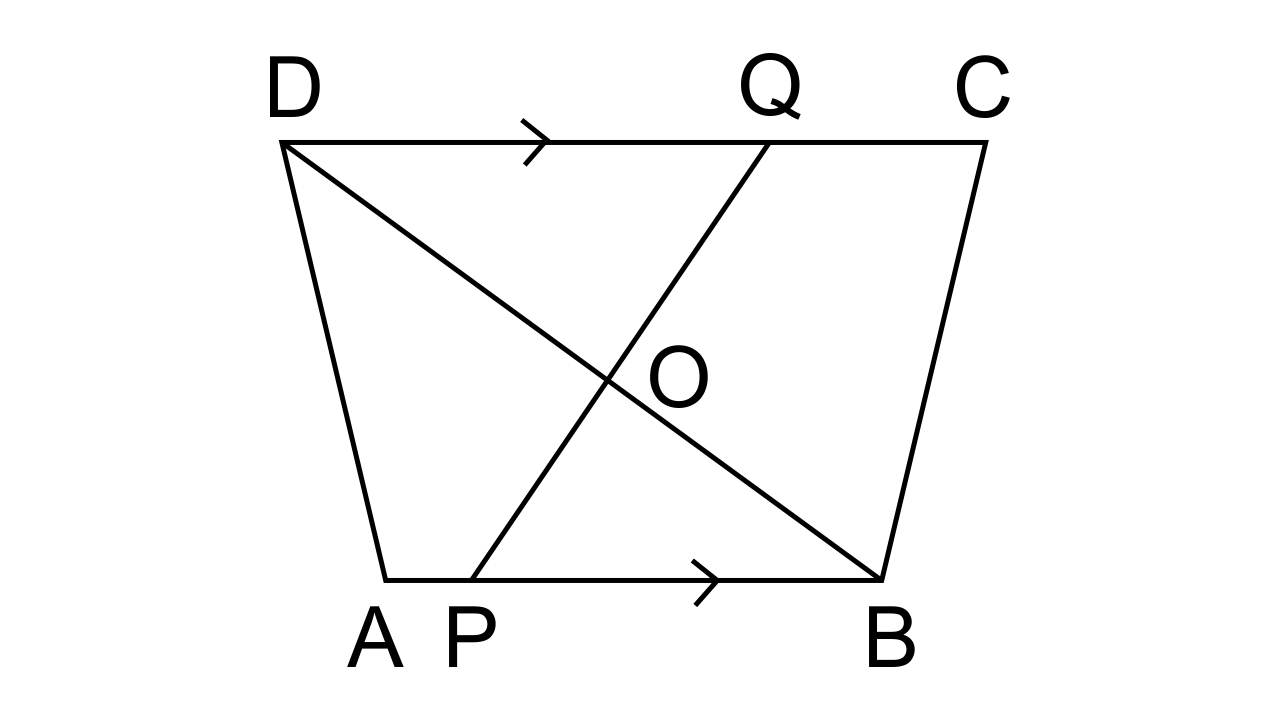
Ans: Let us consider Δ DOQ and Δ BOP, 

∠QDO = ∠PBO (As it given that AB || DC, it also means that PB || DQ)

So ∠DOQ = ∠BOP (As they are vertically opposite angles)

By AA criterion for similarity, we can say that ∆DOQ ~ ∆BOP. 

As the corresponding sides of similar triangles are proportional we have

$\dfrac{{DO}}{{BO}} = \dfrac{{DQ}}{{BP}}$

$\dfrac{{DO}}{6} = \dfrac{{DQ}}{8}$

BP × DO = 48 cm²

10. Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.

Ans: 

Let us consider Δ ABC,

As it’s given that AC = AB

So, ∠ABC = ∠ACB(As angles opposite to equal sides are equal)

In Δ PRC and Δ PQB,

∠ABC = ∠ACB

∠PRC = ∠PQB(As both are right angles)

Hence by the AA criterion for similarity, we can say that ∆PRC ~ ∆PQB

Since corresponding sides of similar triangles are proportional we have

$\dfrac{{PR}}{{PQ}} = \dfrac{{RC}}{{QB}} = \dfrac{{PC}}{{PB}}$

$\dfrac{{PR}}{{PQ}} = \dfrac{{RC}}{{PB}}$

$\dfrac{9}{{15}} = \dfrac{{12}}{{PB}}$

Hence PB = 20 cm

11. State, true or false:

(i) Two similar polygons are necessarily congruent.

Ans:  False

(ii) Two congruent polygons are necessarily similar.

Ans:  True

(iii) All equiangular triangles are similar.

(iv) All isosceles triangles are similar.

(v) Two isosceles-right triangles are similar.

(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.

(vii) The diagonals of a trapezium, divide each other into proportional segments.

Ans:  True

(iv) All isosceles triangles are similar.

Ans:  False

(v) Two isosceles-right triangles are similar.

Ans:  True

(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.

Ans:  True

(vii) The diagonals of a trapezium, divide each other into proportional segments.

Ans:  True

12.Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.Find the lengths of segments DG and DE.

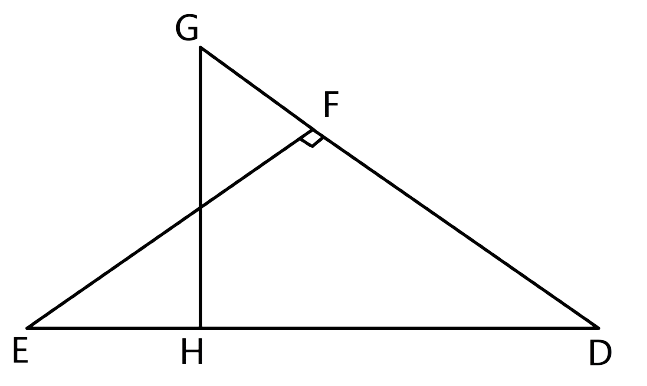
Ans:  Let us consider the Δ DHG and Δ DFE,

∠DFE=∠GHD= 90°

∠D = ∠D(Common)

Hence by the AA criterion for similarity, we can say that ∆DHG ~ ∆DFE

Thus, we have 

$\dfrac{{DH}}{{DF}} = \dfrac{{DG}}{{DE}}$

$\dfrac{8}{{12}} = \dfrac{{(3x - 1)}}{{(4x + 2)}}$

32x + 16 = 36x – 12

28 = 4x

x = 7

Now as its given in the question that 

DG = 3x – 1 and DE = 4x + 2.

DG = 3 × 7 – 1 = 20

DE = 4 × 7 + 2 = 30

13.D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB × CD.

Ans: 

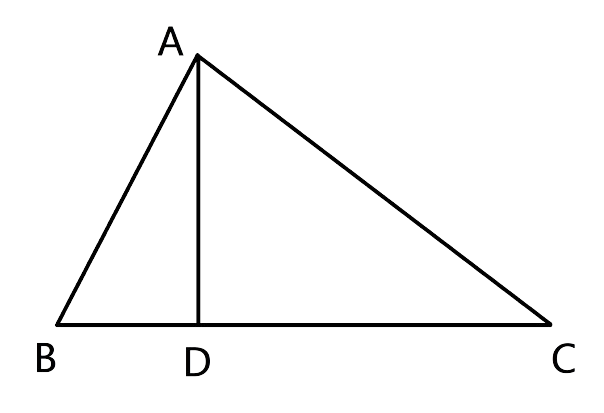
Let us consider Δ ADC and Δ BAC,

From the given information we can say that ∠ADC = ∠BAC

∠ACD = ∠ACB(common angles)

Hence by the AA criterion for similarity, we can say that ∆ADC ~ ∆BAC

Thus, from thus we have 

$\dfrac{{CA}}{{CB}} = \dfrac{{CD}}{{CA}}$which is nothing but, 

$C{A^2}$= CB × CD.

14. In the given figure, ∆ ABC and ∆ AMP are right-angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

(i) ∆ ABC ~ ∆ AMP.

(ii) Find AB and BC.

Ans: 

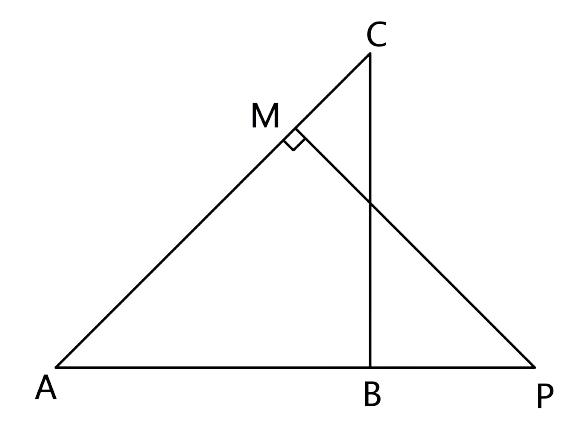
(i) From the figure let us consider ∆ ABC and ∆ AMP, from the triangles we have 

∠BAC = ∠PAM (Common angles)

∠ABC = ∠PMA (Each angle is equal to 90°)

Hence by the AA criterion for similarity, we can say that ∆ABC ~ ∆AMP

(ii) To find AB and BC.

Let us consider the right triangle AMP

By applying Pythagoras theorem, we will have 

AM = 

As earlier we have proven that ∆ABC ~ ∆AMP, we can say that 

$\dfrac{{AB}}{{AM}} = \dfrac{{BC}}{{PM}} = \dfrac{{AC}}{{AP}}$

$\dfrac{{AB}}{9} = \dfrac{{BC}}{{12}} = \dfrac{{10}}{{15}}$

$\dfrac{{AB}}{9} = \dfrac{{10}}{{15}}$

Hence, AB = 6 cm

$\dfrac{{BC}}{{12}} = \dfrac{{10}}{{15}}$

BC = 8 cm

15.Given: RS and PT are altitudes of ΔPQR prove that:

(i) ΔPQT ~ ΔQRS,

(ii) PQ x QS = RQ x QT.

Ans: 

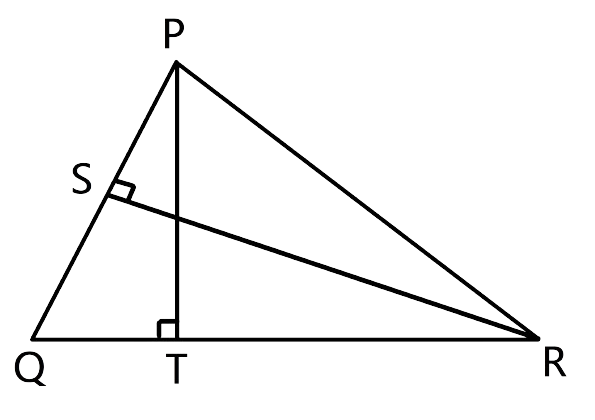
Proof: 

Given, RS and PT are altitudes of ΔPQR 

From the figure let us consider ΔPQT and ΔQRS, 

∠PTQ = ∠RSQ as they are equal to 90°

∠Q = ∠Q (Common angles)

Hence by the AA criterion for similarity, we can say that ΔPQT ~ ΔQRS

$\dfrac{{PQ}}{{RQ}} = \dfrac{{QT}}{{QS}}$

PQ × QS = RQ × QT, hence proved. 

16.Given: ABCD is a rhombus, DPR and CBR are straight lines.

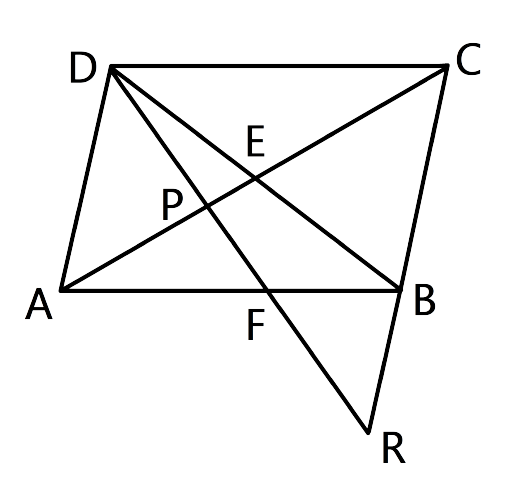
Prove that: DP × CR = DC × PR.

Ans: Let us consider the triangles ΔAPD and ΔPRC 

∠CPR=∠DPA as they are vertically opposite angles 

∠PAD = ∠PCR as they are alternate angles 

Hence by the AA criterion for similarity, we can say that ΔAPD ~ ΔPRC

Thus, $\dfrac{{DP}}{{PR}} = \dfrac{{AD}}{{CR}}$

$ \Rightarrow \dfrac{{DP}}{{PR}} = \dfrac{{DC}}{{CR}}$

Hence, AD=DC 

$ \Rightarrow $DP CR = DC PR(sides of the rhombus)

Hence proved 

17.Given: FB = FD, AE ⊥ FD and FC ⊥ AD.

Prove:$\mathbf{\dfrac{{FB}}{{AD}} = \dfrac{{BC}}{{ED}}}$

Ans:

 

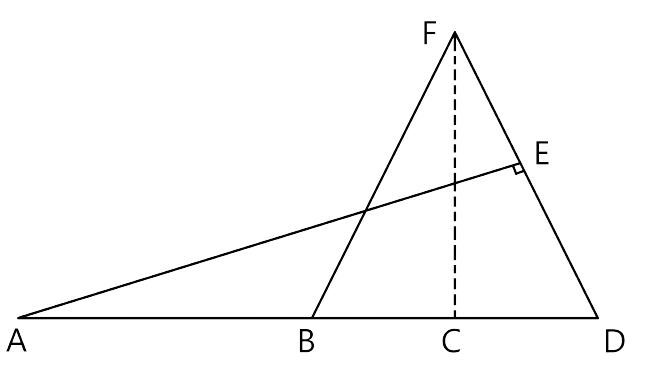
Let us consider the Δ FBC and ΔADE

∠FCB=∠AED(As each angle is equal to 90°)

∠FBC = ∠ADE(As FB=FD)

Hence by the AA criterion for similarity, we can say that Δ FBC ~ ΔADE

Therefore, $\dfrac{{FB}}{{AD}} = \dfrac{{BC}}{{ED}}$

18.In ΔPQR, ∠Q = 90° and QM is perpendicular to PR, Prove that:

(i) PQ² = PM × PR

(ii) QR² = PR × MR

(iii) PQ² + QR² = PR²

Ans: 

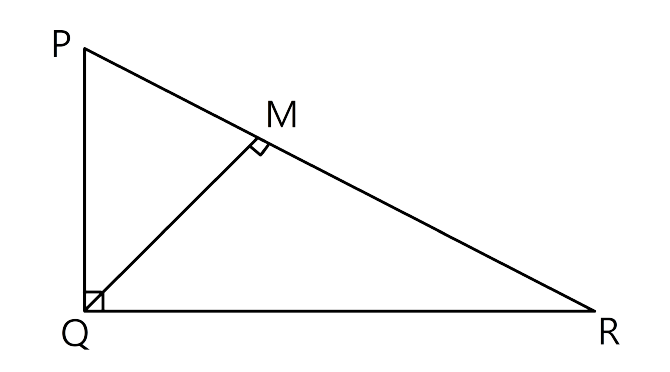
It is given that in ΔPQR, ∠Q =90° and QM ⊥ PR.

Let us consider that triangles ΔPQM and ΔPQR

∠QMP = ∠PQR(As each angle is equal to 90°)

∠P = ∠P

Hence by the AA postulate, we can say that ΔPQM ~ ΔPQR

As ΔPQM ~ ΔPQR, now we can say that 

$\dfrac{{PQ}}{{PR}} = \dfrac{{PM}}{{PQ}}$

PQ² = PM × PR let us consider this to be (i)

Now consider the triangles Δ QRM and Δ PQR,

∠QMR= ∠Q (As each angle is equal to 90°)

∠R=∠R

Therefore, we can say that Δ QRM ~Δ PQR(by the AA postulate)

$\dfrac{{QR}}{{PR}} = \dfrac{{MR}}{{QR}}$

QR² = PR × MR let us consider this to be (ii)

On adding (i) and (ii) we get 

PQ² + QR² = PR²

19.In ΔABC, ∠B = 90° and BD x AC.

(i) If CD = 10 cm and BD = 8 cm; find AD.

(ii) If AC = 18 cm and AD = 6 cm; find BD.

(iii) If AC = 9 cm, AB = 7 cm; find AD

Ans: 

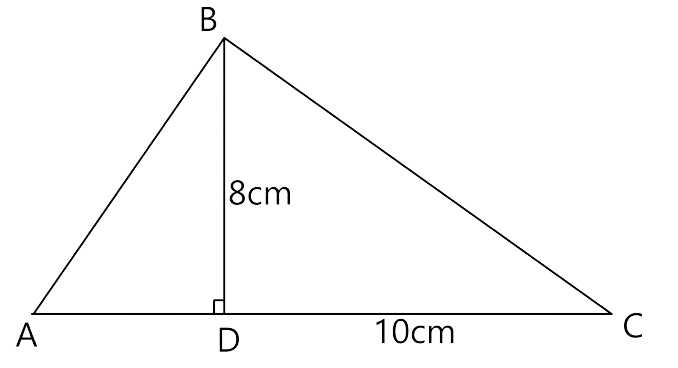
Given that in ΔABC, ∠B = 90°

∠A + ∠C = 90° let this be …….(i)

In ΔBDC, ∠D = 90°

∠CBD + ∠C = 90° let this be ….(ii)

By equating (i) and (ii)

∠A + ∠C = ∠CBD + ∠C

∠A = ∠CBD

Similarly,∠C = ∠ABD

Now let us consider ΔABD and ΔCBD,

∠A = ∠CBD and ∠ABD = ∠C

By AA Postulate we can say that ΔABD ~ ΔCBD

∴$\dfrac{{BD}}{{CD}} = \dfrac{{AD}}{{BD}} = \dfrac{{AB}}{{AC}}$……….……. (i)

$ \Rightarrow B{D^2}$=AD×CD

In the question its given that CD = 10 cm and BD = 8 cm, so 

AD= 6.4 cm 

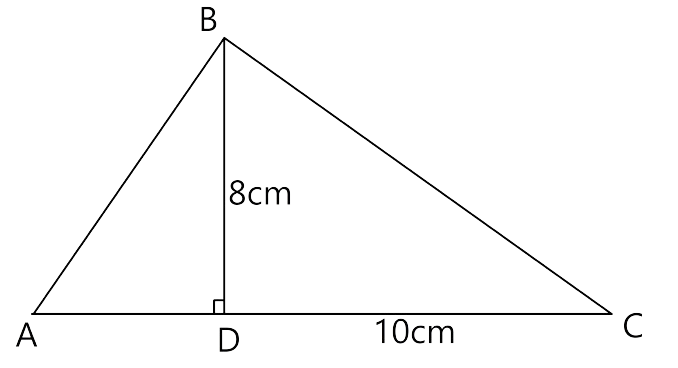
(ii) Let us consider$B{D^2}$=AD×CD, it is also given that 

AC = 18 cm and AD = 6 cm

Substitute the values of AD and CD in $B{D^2}$=ADCD, we have 

$B{D^2}$= 6 12 = 72 

BD = 8.5 cm 

(iii) In ΔABD and Δ ABC 

∠ADB=∠ABC(As its equal to 90°)

∠A = ∠A

By AA postulate we can say that ΔABD ~ Δ ABC 

∴$\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}} = \dfrac{{A{B^2}}}{{AC}}$= AD 

$ \Rightarrow $AD = $\dfrac{{49}}{9}$

20.In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

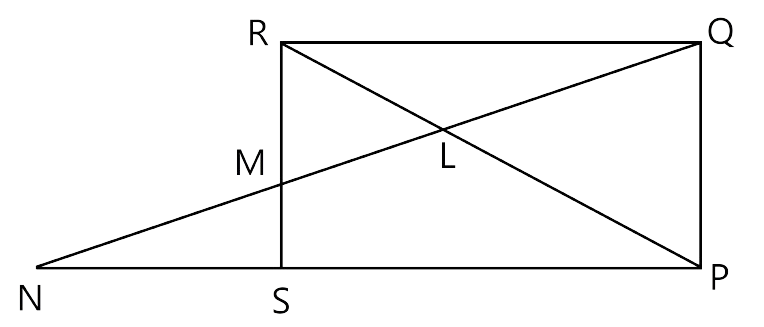
Find the lengths of PN and RM.

Ans: Let us consider ΔLNP and ΔRLQ

∠LNP = ∠LQR(Alternate angles)

∠NLP = ∠QLR (Vertically opposite angles)

By AA Postulate we can say that ΔLNP ~ ΔRLQ

∴$\dfrac{{PN}}{{QR}} = \dfrac{{LP}}{{RL}}$

$\dfrac{{PN}}{{10}} = \dfrac{3}{2}$

PN = 15 cm. 

Similarly, we can prove that Δ LPQ and Δ LMR.

$\dfrac{{RM}}{{QP}} = \dfrac{{RL}}{{LP}}$

RM =$\dfrac{3}{2}$cm 

21.In quadrilateral ABCD, diagonals AC and BD intersect at point E. Such that AE : EC = BE : ED. Show that ABCD is a parallelogram.

Ans: 

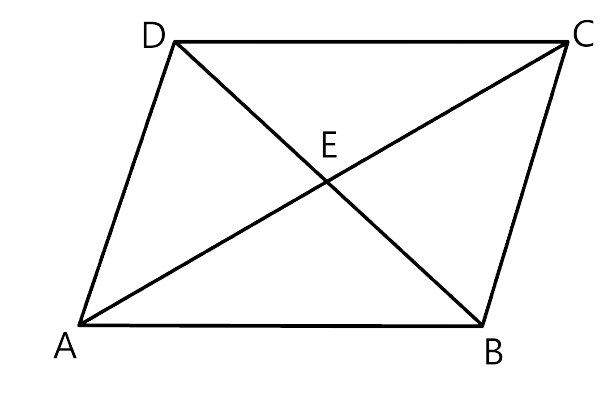
As it is given in quadrilateral ABCD, diagonal AC and BD intersect each other at E and

 In AE : EC = BE : ED

$\dfrac{{EA}}{{EC}} = \dfrac{{BE}}{{ED}}$

$\dfrac{{EA}}{{BE}} = \dfrac{{EC}}{{ED}}$

In Δ AEB and Δ CED

$\dfrac{{AE}}{{BE}} = \dfrac{{EC}}{{ED}}$

∠AEB = ∠CED(As they are vertically opposite angles)

ΔAEB ~ ΔCED(by SAS axiom)

∠EAB = ∠ECB

∠EBA = ∠CDE, as these are pairs of alternate angles

AB || CD …. (i)

Similarly, we can prove that

AD || BC …. (ii)

from (i) and (ii)

ABCD is a parallelogram.

22.  In ΔABC, AD is perpendicular to side BC and AD² = BD × DC. Show that angle BAC = 90°

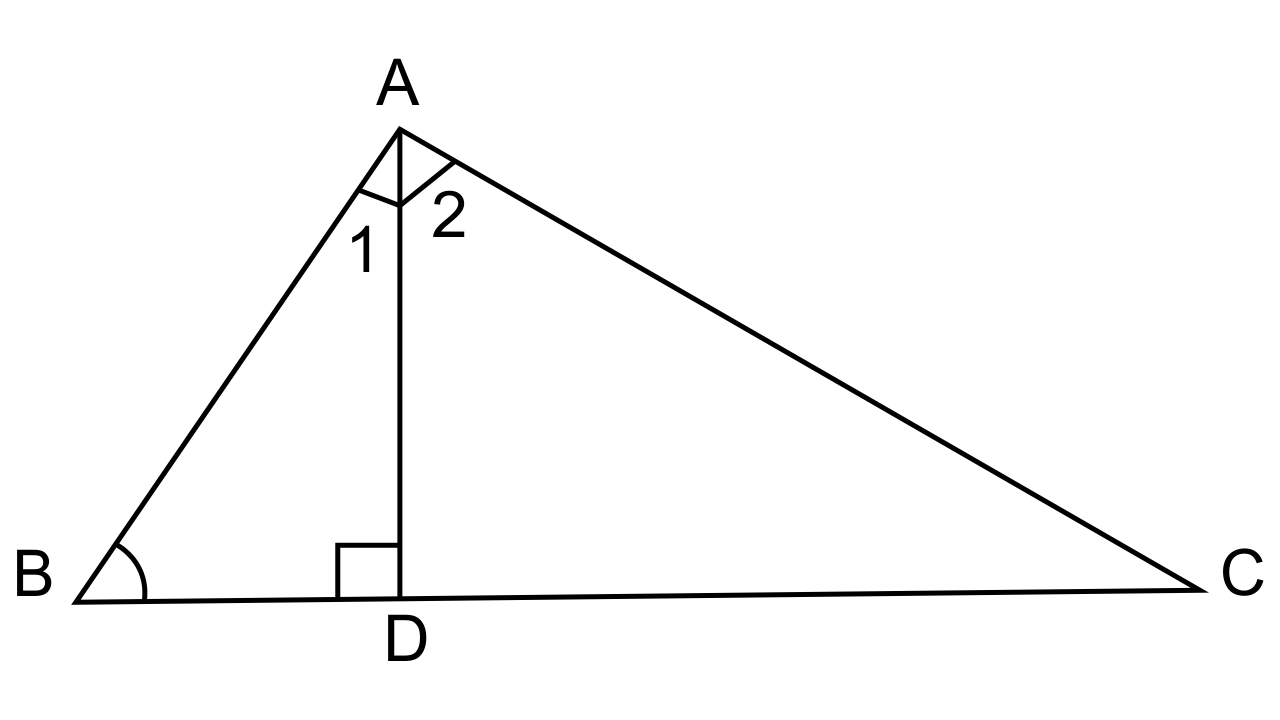
Ans: It is given that ΔABC, AD × BC and AD² = BD × DC

To Prove: ∠BAC = 90°

AD² = BD × DC 

$\dfrac{{AD}}{{DC}} = \dfrac{{BD}}{{AD}}$

Now in Δ ABD and ΔACD, 

$\dfrac{{AD}}{{DE}} = \dfrac{{BD}}{{AD}}$(Given information)

∠ADB = ∠ADC (As they are equal to 90°)

∴ By SAS Postulate we can say that ΔADB ~ Δ ACD

∴∠B = ∠DAC……...(i)

And ∠BAD = ∠C……...(ii)

Add (i) and (ii)

∠B + ∠C= ∠DAC+ ∠BAD= ∠BAC= ∠A

But ∠A + ∠B + ∠C =180° (Angles of the triangle)

∠A+∠A=180°

∠A = 90° or we could say ∠BAC = 90° 

23.In the given figure AB || EF || DC; AB = 67.5 cm. DC = 40.5 cm and AE = 52.5 cm.

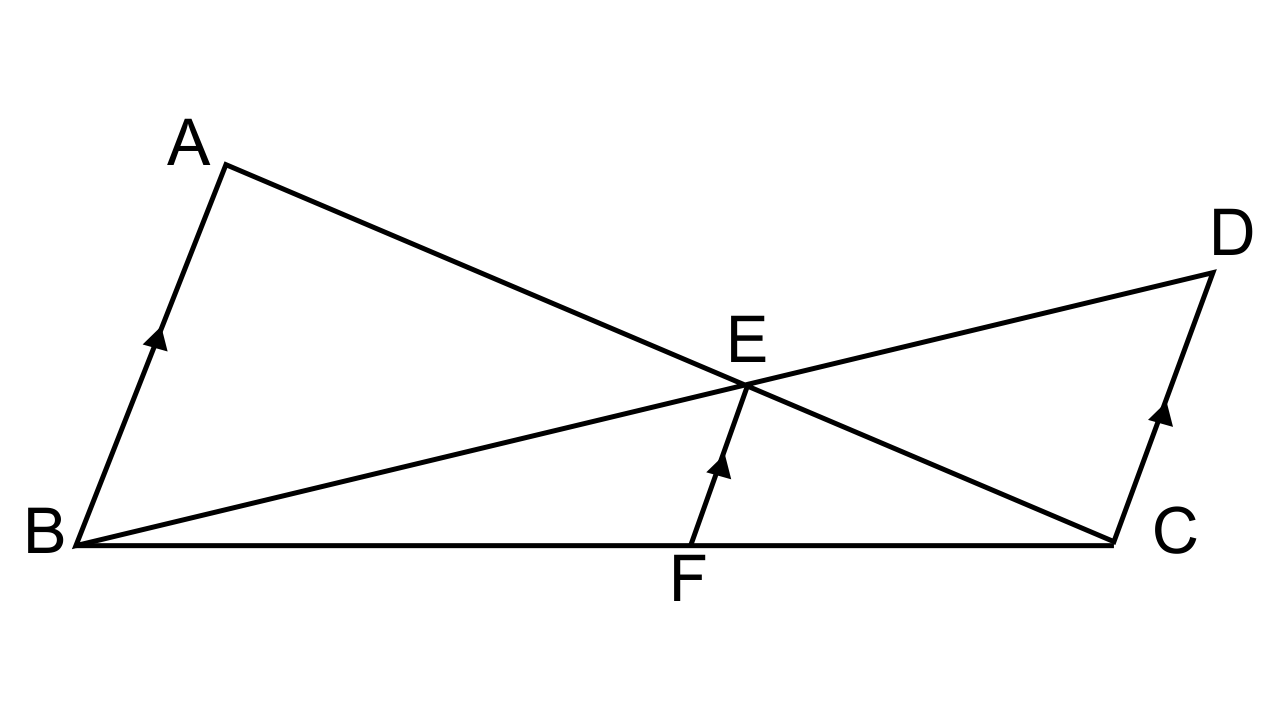
(i) Name the three pairs of similar triangles.

(ii) Find the lengths of EC and EF

Ans: (i) In the figure AB || EF || DC

There are three pairs of similar triangles.

(i) ΔAEB ~ ΔDEC

(ii) ΔABC ~ ΔEEC

(iii) ΔBCD ~ ΔEBF

(ii) ΔAEB ~ ΔDEC

∴$\dfrac{{EA}}{{EC}} = \dfrac{{BE}}{{EB}} = \dfrac{{AB}}{{DC}}$

It is given that AB = 67.5 cm. DC = 40.5 cm and AE = 52.5 cm.

∴$\dfrac{{52.5}}{{EC}} = \dfrac{{7.5}}{{40.5}}$

EC = 31.5 cm 

In ΔABC, EF ||AB

∴$\dfrac{{AC}}{{EC}} = \dfrac{{AB}}{{EF}}$

$\dfrac{{84}}{{31.5}} = \dfrac{{67.5}}{{EF}}$

EF=$\dfrac{{405}}{{16}}$

24. In the given figure, QR is parallel to AB and DR is parallel to QB.

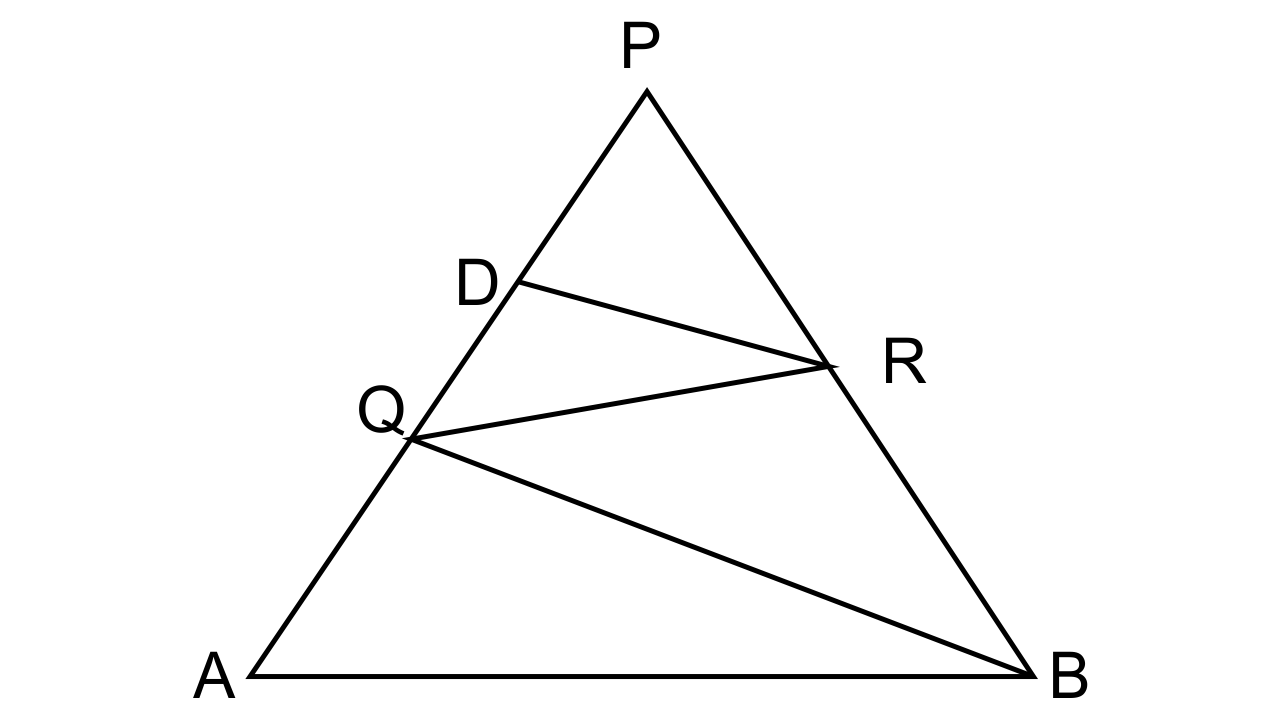
Prove that PQ² = PD × PA.

Ans: Given that in the figure QR is parallel to AB and DR is parallel to QB.

To prove that PQ² = PD × PA.

Let us consider ΔPQB

DR || QB

∴ PD/PQ = PR/PB……....(i)

In ΔPAB

QR || AB

$\dfrac{{PQ}}{{PA}} = \dfrac{{PR}}{{PB}}$………......(ii)

From (i) and (ii)

$\dfrac{{PD}}{{PQ}} = \dfrac{{PQ}}{{PA}}$

PQ² = PD × PA.

25. Through the midpoint M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E.

Prove that: EL = 2 BL.

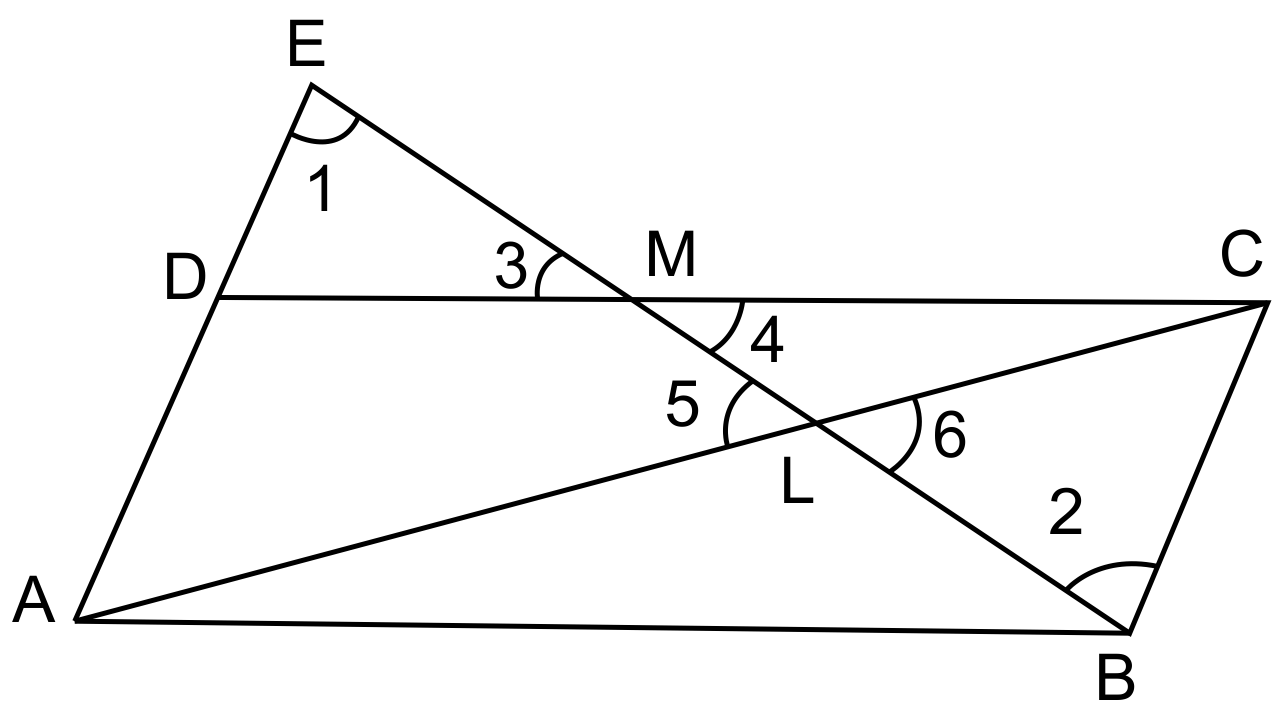
Ans: In parallelogram ABCD, M is the mid-point A of CD.

AC is the diagonal.

BM is joined and produced meeting AD produced in E and, intersecting AC in L.

To Prove: EL = 2 BL.

Proof: In ΔEDM, and ΔMBC,

DM = MC (M is midpoint of DC)

∠EMD = ∠CMD (vertically opposite angles)

∠EDM = ∠MCB (Alternate angles)

ΔEDM = ΔMBC (ASA postulate of congruence)

ED = CB = AD

EA = 2 AD = 2 BC

AB = BC(Opposite sides of the parallelogram)

∠DEM = ∠MBC

Now in ΔELA and ΔBLC,

∠ELA = ∠BLC (vertically opposite angles)

∠DEM or ∠AEL = ∠LBC (proved)

ΔELA ~ ΔBLC (AA postulate)

∴$\dfrac{{EA}}{{BC}} = \dfrac{{EL}}{{LB}}$

$\dfrac{{2BC}}{{BC}} = \dfrac{{EL}}{{LB}}$

EL=2LB

∴ EL=2BL

26. In the figure given below P is a point on AB such that AP: PB = 4 : 3. PQ is parallel to AC.

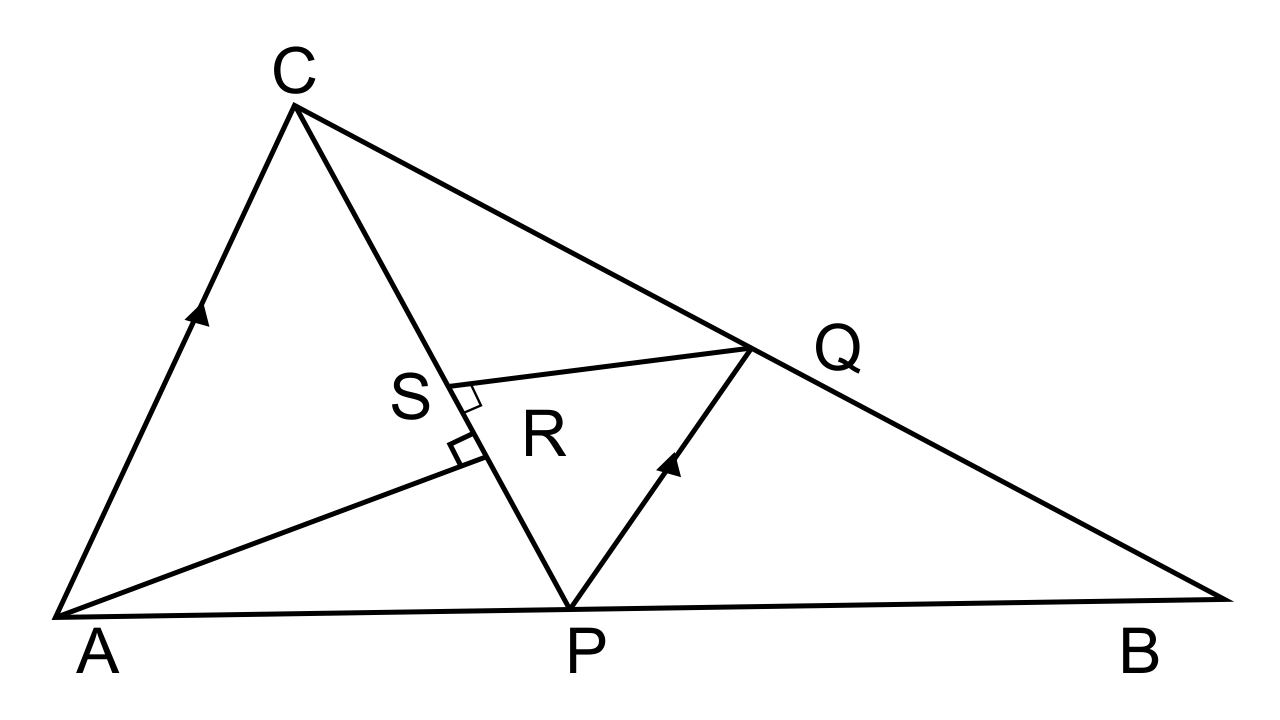
(i) Calculate the ratio PQ: AC, giving the reason for your answer.

(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°.

Given QS = 6 cm, calculate the length of AR.

Ans: It is been given that, In ΔABC, P is a point on AB such that AP: PB = 4 : 3

and PQ || AC is drawn meeting BC in Q. It is also given that CP is joined and QS ⊥ CP and AR ⊥ CP

(i) In ΔABC, PQ || AC

= $\dfrac{{PQ}}{{AC}} = \dfrac{{BP}}{{AB}} = \dfrac{{BP}}{{BP + AP}} = \dfrac{3}{{3 + 4}} = \dfrac{3}{7}$

PQ: AC =3:7

(ii) Now let us consider ΔARC and ΔPSQ

∠ARC= ∠PSQ (As each is equal to 90°)

∠ACR= ∠QPS (Alternate angles)

Hence by AA postulate, we can say that, ΔARC ~ ΔPSQ

∴$\dfrac{{AC}}{{PQ}} = \dfrac{{AR}}{{QS}}$

We know that$\dfrac{{PQ}}{{AC}} = \dfrac{3}{7}$, QS = 6 cm

$\dfrac{{AC}}{{PQ}} = \dfrac{{AR}}{{QS}}$

$\dfrac{7}{3} = \dfrac{{AR}}{6}$

AR = 14 cm. 

The length of side AR is 14 cm

27. In the right-angled triangle QPR, PM is an altitude.

Given that QR = 8 cm and MQ = 3.5 cm. Calculate the value of PR.

Given: In right-angled ΔQPR, ∠P = 90° PM ⊥ QR, QR = 8 cm, MQ = 3.5 cm. Calculate PR

Ans: Let us consider ΔPQM and ΔQPR

∠PMQ = ∠QPR (each angle is equal to 90°)

∠Q = ∠Q 

Hence by AA postulate, we can say that, ΔPQM ~ ΔQPR 

∴$\dfrac{{PQ}}{{QR}} = \dfrac{{QM}}{{PQ}} = \dfrac{{PM}}{{PR}}$let us consider this as an equation (i)

$P{Q^2}$= QRQM = 8 3.5= 28

PQ =$\sqrt {28} $let us consider this as an equation (ii)

In ΔPQR, ∠P = 90° and we know that PM ⊥ QR

∴$P{\text{ }}{{\text{M}}^2}$=MR×QM = 3.5 4.5

PM=$\sqrt {3.5 \times 4.5} $ let us consider this as an equation   (iii)

Let us consider equation (i)

$\dfrac{PQ}{QR}=\dfrac{QM}{PQ}=\dfrac{PM}{PR}$

$\dfrac{{\sqrt {28} }}{8} = \dfrac{{\sqrt {3.5 \times 4.5} }}{{P{R^2}}}$

On squaring both sides and solving it we get 

$P{R^2}$ = 36

PR = 6 cm. 

28. In the figure given below, the medians BD and CE of a triangle ABC meet at G.

Prove that

(i) ΔEGD ~ ΔCGB

(ii) BG = 2 GD from (i) above.

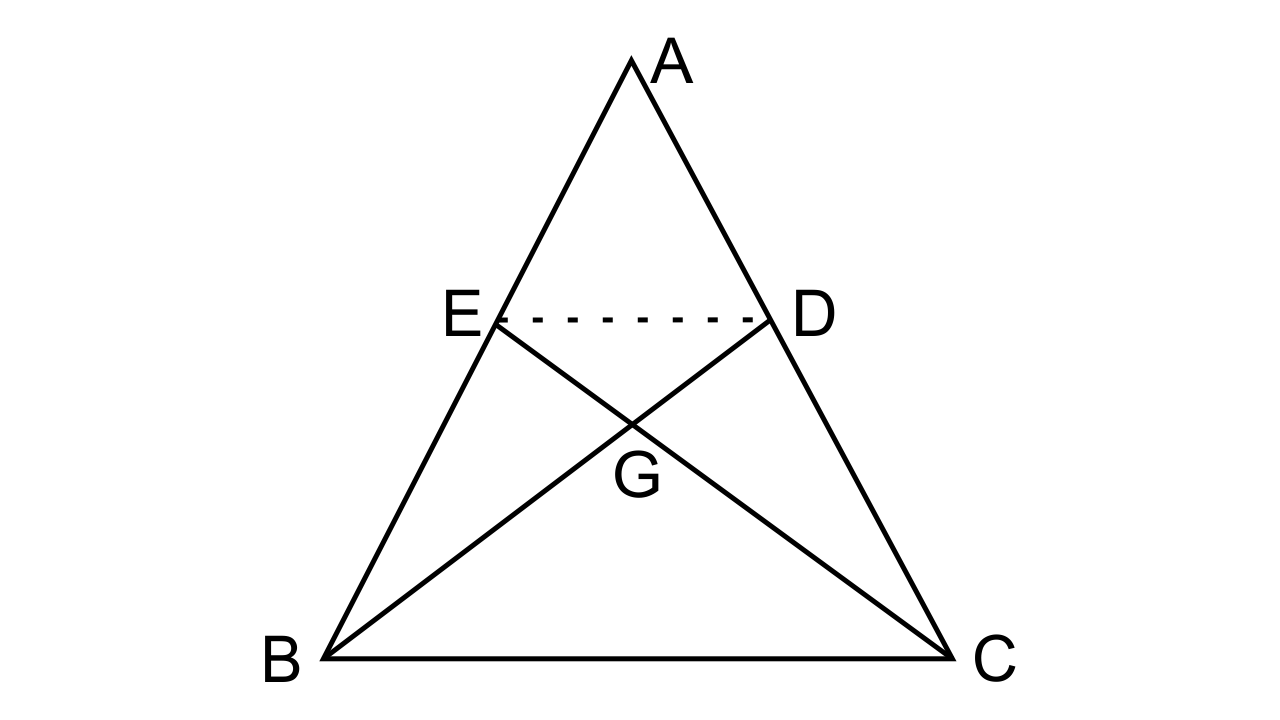
Ans: It is given that In ΔABC, BD and CE are the medians of sides AC and AB respectively which intersect each at G.

To Prove that 

(i) ΔEGD ~ ΔCGB 

From the figure, we can say that D and E are the midpoints of AC and AB respectively.

∴ ED || BC and ED = ½ BC or it can be also represented as 

ED/BC= ½, let this be equation (i)

Now let us consider ΔEGD and ΔCGB 

∠EGD = ∠BCG (As they are vertically opposite angle)

∠EDG = ∠BGG (Alternate angles)

Hence by AA postulate, we can say that, ΔEGD ~ ΔCGB 

∴$\dfrac{{GD}}{{BG}} = \dfrac{{ED}}{{BC}} = \dfrac{1}{2}$

BG = 2 GD, Hence, proved. 

Exercise 15(B) 

1. In the following figure, point D divides AB in the ratio 3: 5. Find:

(i) AE/EC 

(ii) AD/AB 

(iii) AE/ACAlso if,

(iv) DE = 2.4 cm, find the length of BC.

(v) BC = 4.8 cm, find the length of DE.

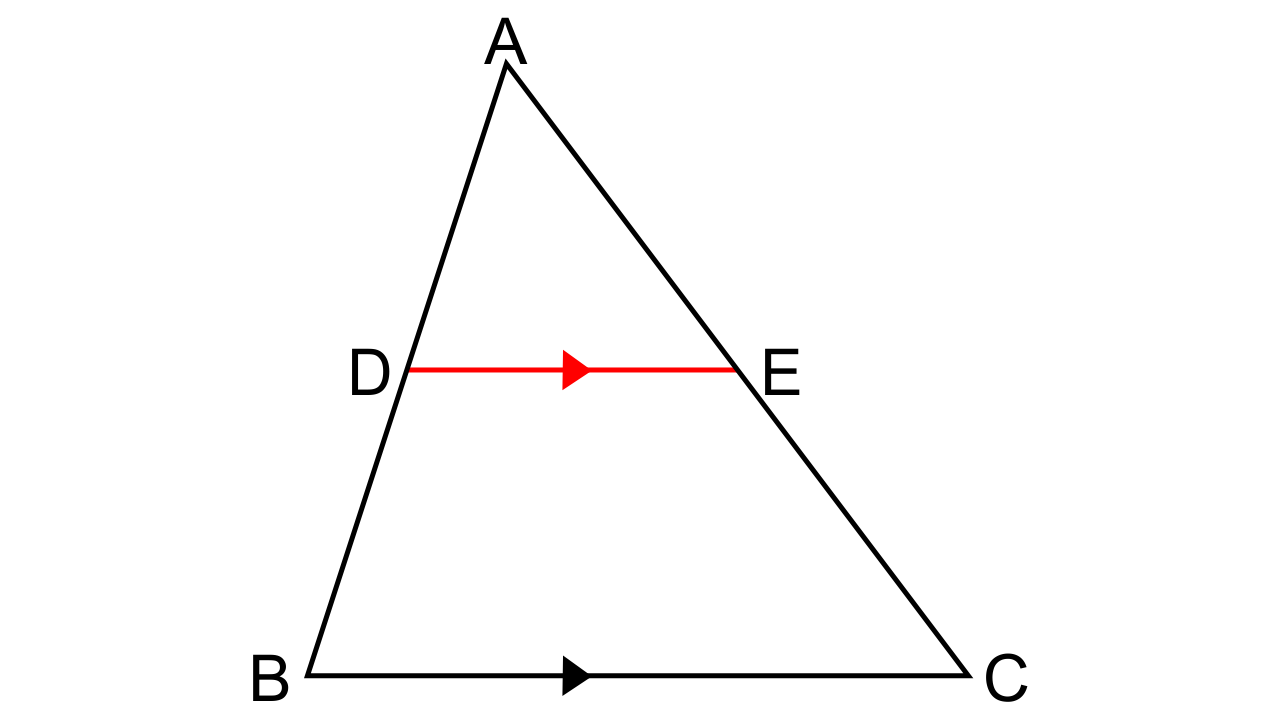
Ans: (i) It is given that $\dfrac{{AD}}{{AB}} = \dfrac{3}{5}$and DE || BC.

By following the Basic Proportionality theorem, we have 

$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{EC}}$

$\dfrac{{AE}}{{EC}} = \dfrac{3}{5}$

(ii)Given that $\dfrac{{AD}}{{AB}} = \dfrac{3}{5}$

Then, $\dfrac{{DB}}{{AD}} = \dfrac{5}{3}$

Add 1 on both sides, we will get 

$\dfrac{{AB}}{{AD}} + 1 = \dfrac{5}{3} + 1$

(DB + AD)/ AD = (5 + 3)/ 3

$\dfrac{{AB}}{{AD}} = \dfrac{8}{3}$

Now, $\dfrac{{AD}}{{AB}} = \dfrac{3}{8}$

(iii) Let us consider ∆ABC in which DE || BC

By following the Basic Proportionality theorem, we have

$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}$

So, $\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}$

$\dfrac{{AD}}{{AB}} = \dfrac{3}{8}$

∴$\dfrac{{AE}}{{AC}} = \dfrac{3}{8}$

(iv) Let us consider ∆ADE and ∆ABC,

∠ADE = ∠ABC(As corresponding angles are equal also as DE || BC)

∠A = ∠A

Hence by AA criterion for similarity, we can say that ∆ADE ~ ∆ABC

Now we have,

$\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}$

$\dfrac{3}{8} = \dfrac{{2.4}}{{BC}}$

BC = 6.4 cm

(v) Since we have proven that ∆ADE ~ ∆ABC due to AA criterion for similarity

We have, 

$\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}$

$\dfrac{3}{8} = \dfrac{{DE}}{{4.8}}$

DE = 1.8 cm

2. In the given figure, PQ ‖ AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find:

(i) $\mathbf{\dfrac{CP}{PA}}$ 

(ii) PQ 

(iii) If AP = x, then the value of AC in terms of x.

Ans:  

It is given that PQ ‖ AB and CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm then 

(i) Let us consider ∆CPQ and ∆CAB,

As PQ || AB, and corresponding angles are equal we can say that ∠PCQ = ∠APQ

∠C = ∠C as its a common angle 

Hence by the AA criterion for similarity, we can say that ∆CPQ ~ ∆CAB

Now we have,

$\dfrac{{CP}}{{AC}} = \dfrac{{CQ}}{{CB}}$

$\dfrac{{CP}}{{AC}} = \dfrac{{4.8}}{{8.4}} = \dfrac{4}{7}$

Thus,$\dfrac{{CP}}{{PA}} = \dfrac{4}{3}$

(ii) As we have proven that ∆CPQ ~ ∆CAB by AA criterion for similarity

We have, 

$\dfrac{{PQ}}{{AB}} = \dfrac{{CQ}}{{CB}}$

$\dfrac{{PQ}}{{6.3}} = \dfrac{{4.8}}{{8.4}}$

PQ = 3.6 cm

(iii)As we have proven that ∆CPQ ~ ∆CAB by AA criterion for similarity

We have,

$\dfrac{{CP}}{{AC}} = \dfrac{{CQ}}{{CB}}$

$\dfrac{{CP}}{{AC}} = \dfrac{{4.8}}{{8.4}} = \dfrac{4}{7}$

So, if CP is 4 parts and AC is 7 parts then we can say that PA is 3 parts

Hence, $AC = \dfrac{7}{3} \times PA = \left(\dfrac{7}{3}\right)x$

3. A-line PQ is drawn parallel to the side BC of Δ ABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.

Ans:  

Let us consider ∆ APQ and ∆ ABC,

As PQ || BC, and corresponding angles are equal we can say that, ∠APQ = ∠ABC

∠PAQ = ∠BAC (Common angles)

Hence by the AA criterion for similarity, we can say that ∆APQ ~ ∆ABC

Now we have,

$\dfrac{{AP}}{{AB}} = \dfrac{{AQ}}{{AC}}$

$\dfrac{{AP}}{9} = \dfrac{{4.2}}{6}$

Thus,

AP = 6.3 cm

4. In Δ ABC, D and E are the points on sides AB and AC respectively.

Find whether DE ‖ BC, if

(i) AB = 9cm, AD = 4cm, AE = 6cm and EC = 7.5cm. 

(ii) AB = 6.3 cm, EC = 11.0 cm, AD =0.8 cm and EA = 1.6 cm.

Ans: (i) Let us consider ∆ ADE and ∆ ABC,

$\dfrac{{AE}}{{EC}} = \dfrac{6}{{7.5}} = \dfrac{4}{5}$

$\dfrac{{AD}}{{BD}} = \dfrac{4}{5}$ (As BD = AB – AD = 9 – 4 = 5 cm)

So,$\dfrac{{AE}}{{EC}} = \dfrac{{AD}}{{BD}}$

∴By the converse of Basic Proportionality theorem, DE || BC

(ii) Let us consider the ∆ ADE and ∆ ABC,

$\dfrac{{AE}}{{EC}} = \dfrac{{1.6}}{{11}} = \dfrac{{0.8}}{{5.5}}$

$\dfrac{{AD}}{{BD}} = \dfrac{{0.8}}{{5.5}}$(As BD = AB – AD = 6.3 – 0.8 = 5.5 cm )

Hence, $\dfrac{{AE}}{{EC}} = \dfrac{{AD}}{{BD}}$

∴By the converse of Basic Proportionality theorem, DE || BC

5. In the given figure, Δ ABC ~ Δ ADE. If AE: EC = 4: 7 and DE = 6.6 cm, find BC. If ‘x’ is the length of the perpendicular from A to DE, find the length of the perpendicular from A to BC in terms of ‘x’.

Ans: 

It is given that, Δ ABC ~ Δ ADE (AA criterion for similarity)

So, we have, 

$\dfrac{{AE}}{{EC}} = \dfrac{{DE}}{{BC}}$

$\dfrac{4}{{11}} = \dfrac{{6.6}}{{BC}}$

$BC = \dfrac{(11 \times 6.6)}{4} = 18.15 cm$

As Δ ABC ~ Δ ADE, we can say that ∠ABC = ∠ADE and ∠ACB = ∠AED

So ∴ DE || BC

And since $\dfrac{{AE}}{{EC}} = \dfrac{4}{7}$, we have$\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}} = \dfrac{{11}}{4}$

Now let us consider ∆ ADP and ∆ ABQ, 

∠ADP = ∠ABQ(Since DP || BQ, corresponding angles are equal)

∠APD = ∠AQB(Since DP || BQ, corresponding angles are equal)

By applying the AA criterion for similarity, we can say that ∆ADP ~ ∆ABQ.

$\dfrac{{AD}}{{AB}} = \dfrac{{AP}}{{AQ}}$

$\dfrac{4}{{11}} = \dfrac{X}{{AQ}}$

Thus,

$AQ = \left(\dfrac{11}{4}\right)x$

6. A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.

Ans:  

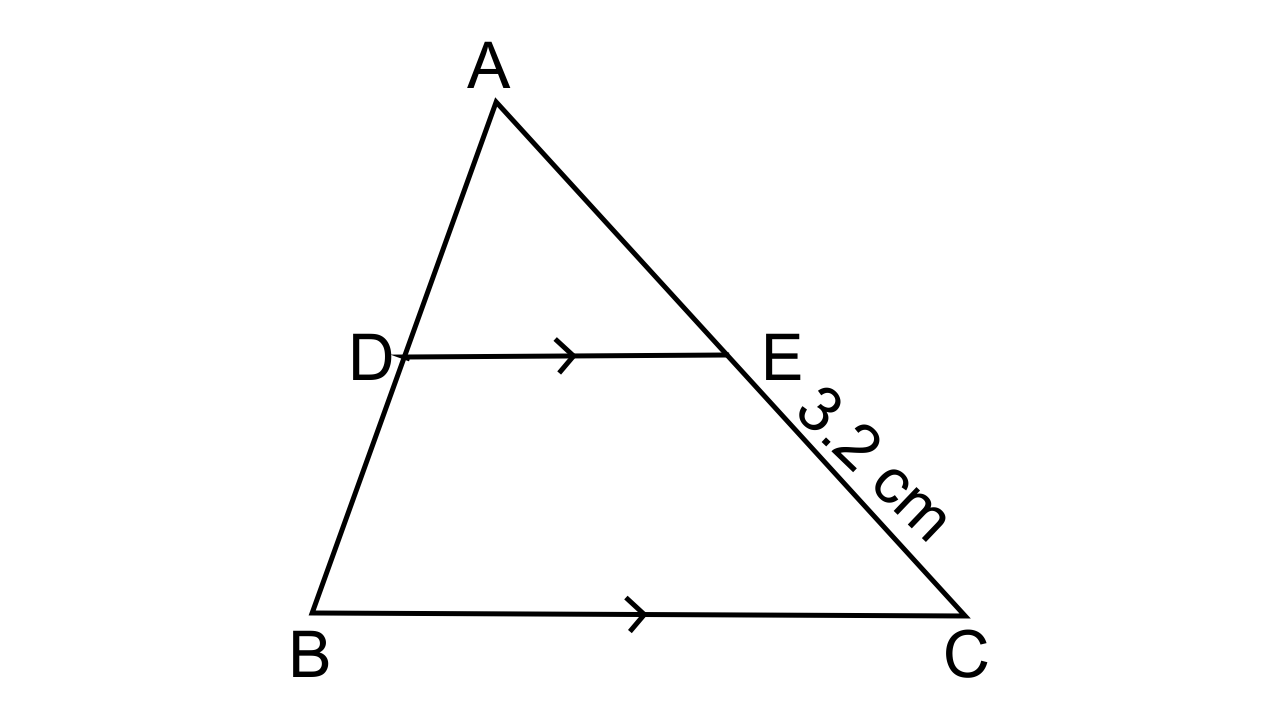
Given that, 

In ΔABC, DE || BC

AB = 5 BD and EC = 3.2 cm

Since it is given that DE || BC

 Hence by the AA criterion for similarity, we can say that ΔADE ~ ΔABC 

∴$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{EC}}$

$\dfrac{4}{1} = \dfrac{{AE}}{{3.2}}$

$AE = \dfrac{12.8}{1} = 12.8 cm$. 

7. In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y. 

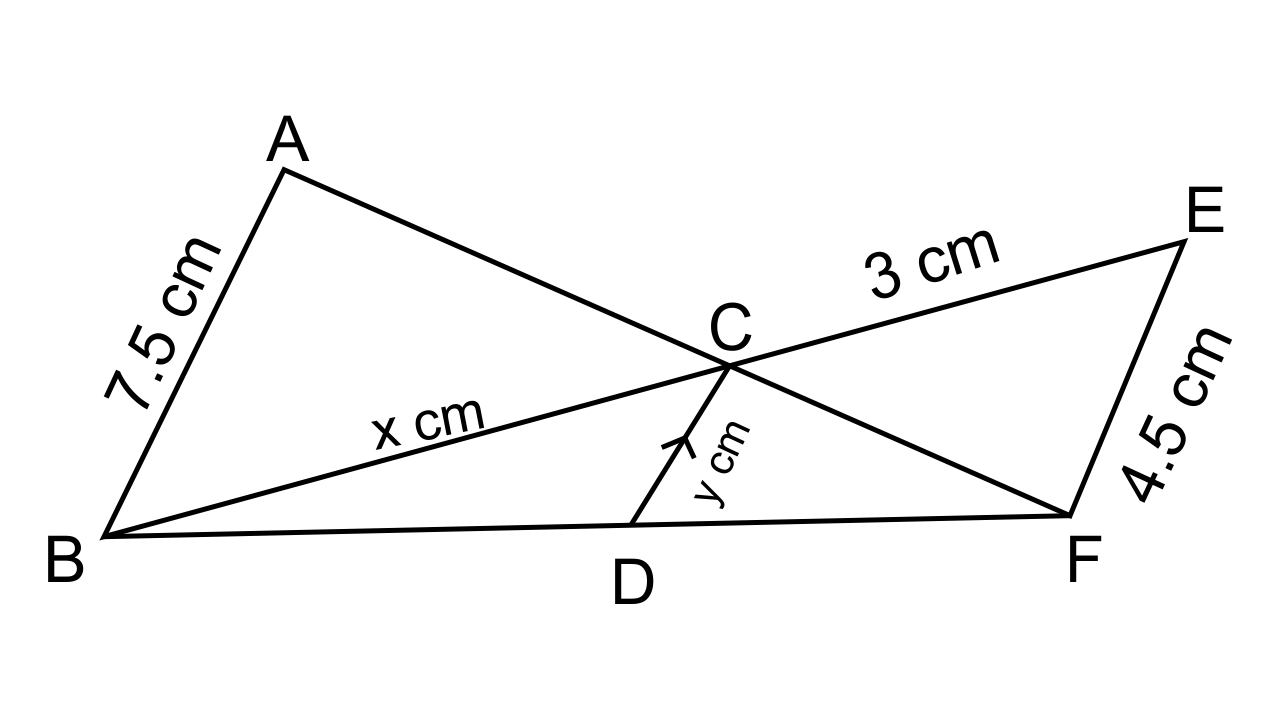
Ans: Let us consider the ΔACB and ΔFCE, in which we have 

∠ACB = ∠FCE(As they are vertically opposite angles)

∠CBA = ∠CEF(Alternate to each other)

Hence, by AA Axiom of similarity, we can say that ΔACB ~ ΔFCE

Thus, the corresponding sides of the triangles are proportional to each other. 

∴$\dfrac{{AB}}{{BC}} = \dfrac{{EF}}{{EC}}$

$ \Rightarrow \dfrac{{7.5cm}}{{xcm}} = \dfrac{{4.5cm}}{{3cm}}$

On solving  x= 5 cm 

Now let us consider ΔEFB and ΔBCD, we have 

∠EFB = ∠DBC (Corresponding angles)

∠BEF = ∠BCD 

∴ By AAA axiom of similarity, we can say that ΔEFB ~ ΔBCD.

Hence,$\dfrac{{EB}}{{CB}} = \dfrac{{4EF}}{{CD}}$

$\dfrac{{EC}}{{CB + CB}} = \dfrac{{4.5cm}}{y}$

$3 + \dfrac{x}{x} = \dfrac{{4.5}}{y}$

On solving and by substituting the value of x= 5 cm here we get, 

y= $\dfrac{{45}}{{16}}$cm

8. In the figure, given below, PQR is a right angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR. 

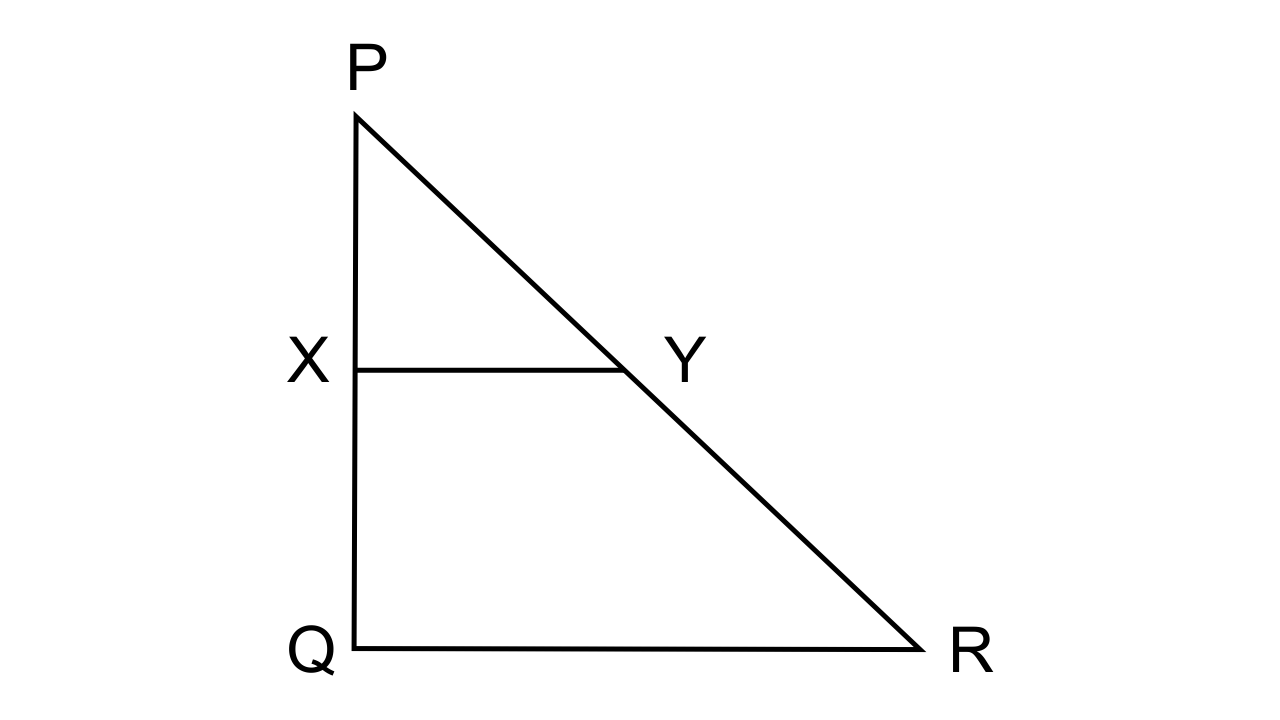
Ans: In the question it is given that PQ = 6 cm; PY = 4 cm, and PX : XQ = 1 : 2

From the figure given it is evident that the line drawn parallel to one side of the triangle divides the other two sides proportionally.

∴we can say that,

$\dfrac{{PX}}{{XQ}} = \dfrac{{PY}}{{YR}} = \dfrac{1}{2} = \dfrac{4}{{YR}}$

Hence, YR = 8 cm.

But PR = PY+ YR

= 4+ 8 = 12 cm 

Let us consider the right angled ΔPQR, and on using the Pythagorean theorem we have 

$Q{R^2} + P{Q^2} = P{R^2}$

QR =$\sqrt {144 - 36}  = 10.392cm$

9. In the following figure, M is the midpoint of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that: PE = 2PD.

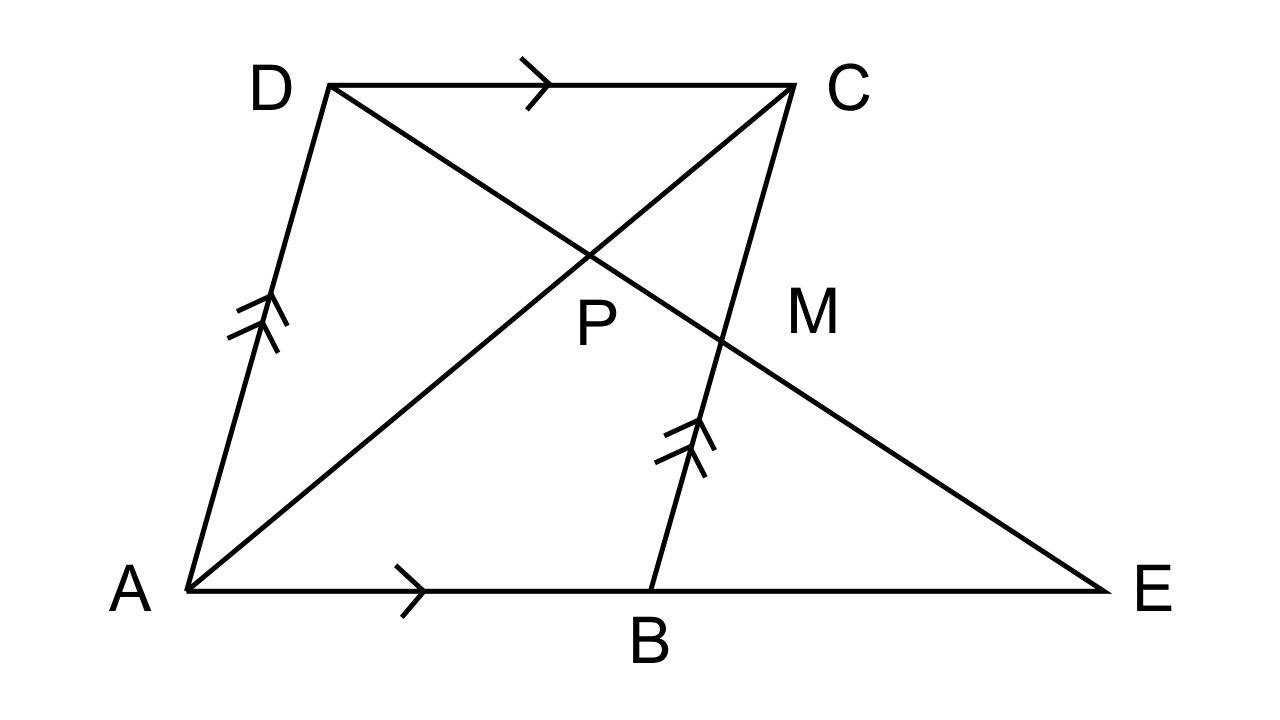
Ans:  Given from the question that, 

Figure, ABCD is a parallelogram 

AB || CD, AD || BC

M is mid point of BC

DM intersect AB produced at E and AC at P

To prove that PE = 2PD

Proof: In ΔDEA, 

AD || BC (As they are opposite sides of the parallelogram) 

M is a mid point of CB B is a mid point of AE 

AB = BE ⇒ AE = 2AB or 2CD

Let us consider ΔPAE and ΔPCD

∠APE = ∠CPD (They are vertically opposite angles)

∠PAE = ∠PCD (Alternate angles)

∴ Hence by the AA criterion for similarity, we can say that ΔPAE ~ ΔPCD

∴$\dfrac{{PE}}{{PD}} = \dfrac{{AE}}{{DC}} \Rightarrow \dfrac{{PE}}{{PD}} = \dfrac{{2DC}}{{DC}}$

∴ PE = 2PD 

Hence proved.

10. The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

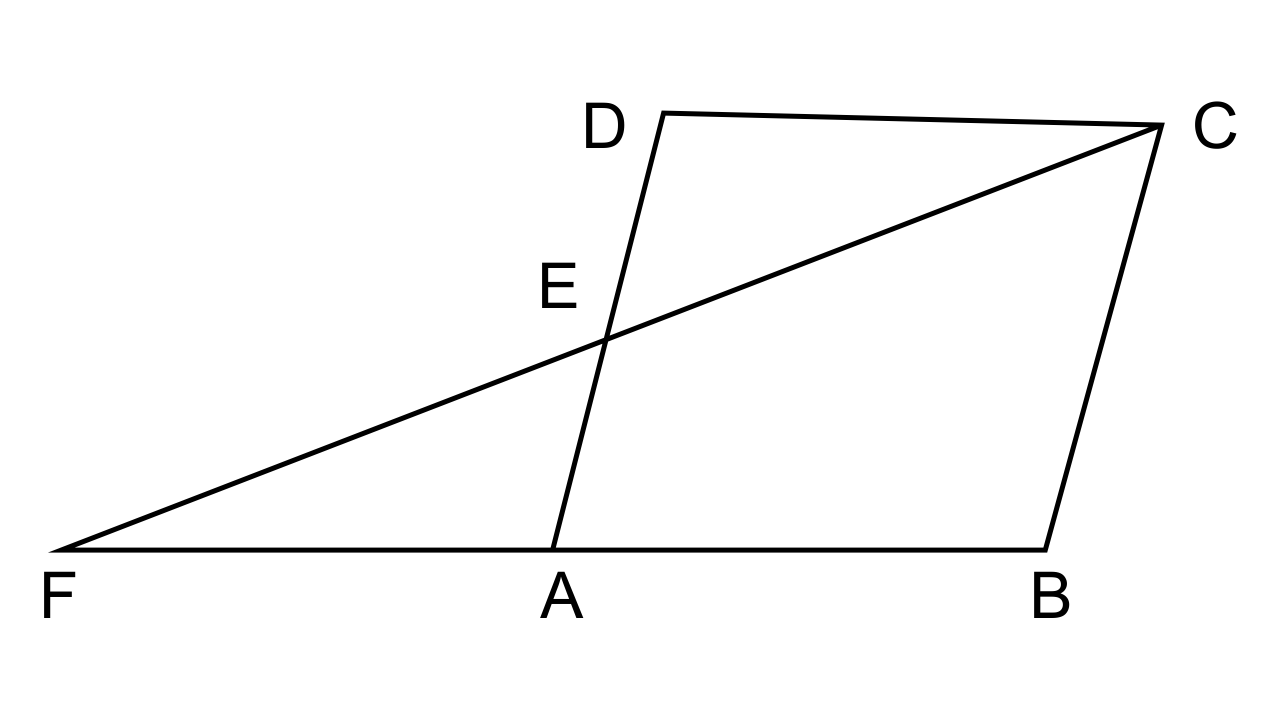
Ans:  It is given that

In the given figure, ABCD is a parallelogram and E is a point on AD 

CE is produced to meet BA produced at point F

AE = 4 cm, AF = 8 cm, AB = 12 cm

We have to find the perimeter of parallelogram ABCD 

Let us consider the ΔFBC, 

AD or AE || BC (As they are the opposite sides of the parallelogram)

∴ Hence by the AA criterion for similarity, we can say that  ΔAFE  ~  ΔFBC

∴$\dfrac{{FA}}{{FB}} = \dfrac{{AE}}{{BC}} = \dfrac{8}{8} + 12 = \dfrac{4}{{BC}}$

$ \Rightarrow \dfrac{8}{{20}} = \dfrac{4}{{BC}}$

\[\angle APC{\text{ }} = \angle BPD{\text{ }}\left( {Vertically{\text{ }}opp.{\text{ }}angles} \right)BC = 4 \times \dfrac{20}{8} = 10\] 

Perimeter of parallelogram ABCD = 2 (AB + BC) = 2 (12 + 10) cm = 2 × 22 = 44 cm.

Exercise 15(C) 

1. (i) The ratio between the corresponding sides of two similar triangles is 2: 5. Find the ratio between the areas of these triangles.

(ii) Areas of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.

Ans: 

It is given that the ratio between the corresponding sides of two similar triangles is 2: 5.

As we all know, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. Hence, from the above statement, we can say that,

(i) The required ratio is given by,

$\dfrac{{{2^2}}}{{{5^2}}} = \dfrac{4}{{25}}$

(ii) It is given that areas of two similar triangles are 98 sq. cm and 128 sq. cm. 

Now the required ratio is given by,

$\sqrt {\dfrac{{98}}{{128}}}  = \sqrt {\dfrac{{49}}{{64}}}  = \sqrt {\dfrac{7}{8}} $

2.A line PQ is drawn parallel to the base BC of Δ ABC which meets sides AB and AC at points P and Q respectively. If AP = $\dfrac{1}{3}$ PB; find the value of:

(i) Area of Δ ABC/ Area of Δ APQ

(ii) Area of Δ APQ/ Area of Trapezium PBCQ

Ans: It is given that, $AP = \left(\dfrac{1}{3}\right) PB$

Thus, $\dfrac{AP}{PB} = \dfrac{1}{3}$

Let us consider ∆ APQ and ∆ ABC,

As its mentioned that PQ || BC, we can say that corresponding angles are equal

∠APQ = ∠ABC and 

∠AQP = ∠ACB

Hence by AA criterion for similarity, we can say that ∆APQ ~ ∆ABC

So now, 

(i) Area of Δ ABC/ Area of Δ APQ = $\dfrac{{A{B^2}}}{{A{P^2}}}$= 16: 1

(ii) Area of Δ APQ/ Area of Trapezium PBCQ 

= Area of Δ APQ/(Area of Δ ABC – Area of Δ APQ)

= $\dfrac{1}{\dfrac{16}{1}} = 1: 16$

3.The perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.

Ans: It is given that the perimeters of two similar triangles are 30 cm and 24 cm.So let the triangles be ∆ABC and ∆DEF

Let ∆ABC ~ ∆DEF

As they are similar, $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}} = \dfrac{{(AB + BC + AC)}}{{(DE + EF + DF)}}$

= Perimeter of Δ ABC/Perimeter of Δ DEF

Perimeter of Δ ABC/Perimeter of Δ DEF = $\dfrac{{AB}}{{DE}}$

$\dfrac{30}{24} = \dfrac{12}{DE}$

DE = 9.6 cm

4.In the given figure, AX: XB = 3: 5.

Find:(i) the length of BC, if the length of XY is 18 cm.

(ii) the ratio between the areas of trapezium XBCY and triangle ABC.

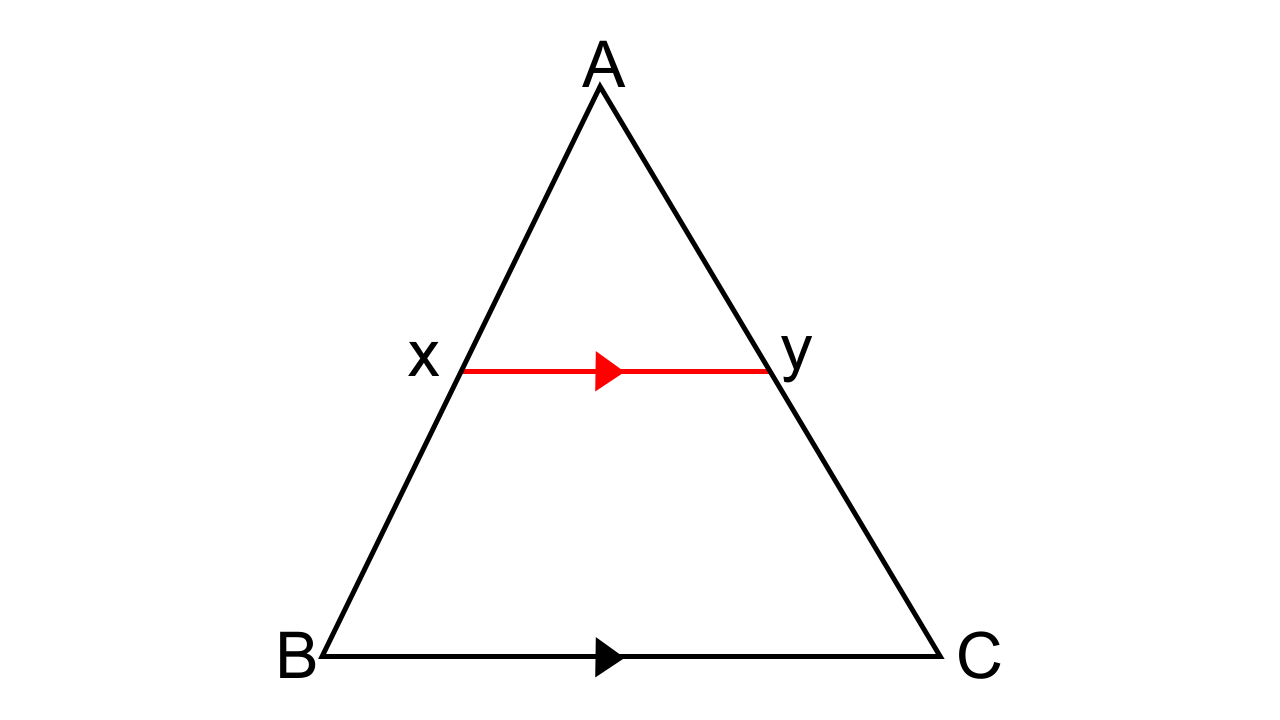
Ans: It is given in the question that $ \Rightarrow $

Now, $\dfrac{X}{{AB}} = \dfrac{3}{8}$……. (1)

(i) To find the length of BC, if the length of XY is 18 cm.

Let us consider Δ AXY and Δ ABC, 

As BC || XY, then corresponding angles are also equal.

∠AXY = ∠ABC and ∠AYX = ∠ACB

Hence by AA criterion for similarity, we can say that ∆AXY ~ ∆ABC

So now we have, 

$\dfrac{{AX}}{{AB}} = \dfrac{{XY}}{{BC}}$

$\dfrac{3}{8} = \dfrac{{18}}{{BC}}$

BC = 48 cm

(ii)  To find the ratio between the areas of trapezium XBCY and triangle ABC.

$\dfrac{{Area{\text{ of }}\Delta {\text{AXY}}}}{{Area{\text{ of }}\Delta {\text{ABC}}}} = \dfrac{{AX2}}{{AB2}} = \dfrac{9}{{64}}$

$\dfrac{{Area{\text{ of }}\Delta {\text{ABC  -  }}Area{\text{ of }}\Delta {\text{AXY}}}}{{Area{\text{ of }}\Delta {\text{ABC}}}} = \dfrac{{(64 - 9)}}{{64}} = \dfrac{{55}}{{64}}$

$\dfrac{{Area{\text{ of trapezium XBCY }}}}{{Area{\text{ of }}\Delta {\text{ABC}}}} = \dfrac{{55}}{{64}}$

5.ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.

Ans:  

It is given that in ΔABC, PQ || BC in such a way that area APQ = area PQCB. We have to find- The ratio of BP : AB.

Area of (Δ APQ) = $\dfrac{1}{2}$ Area of (Δ ABC) which could be also written as 

Area of (Δ APQ)/Area of (Δ ABC) = $\dfrac{1}{2}$

$\dfrac{{A{P^2}}}{{A{B^2}}} = \dfrac{1}{2}$

$\dfrac{{AP}}{{AB}} = \dfrac{1}{{\sqrt 2 }}$

$\dfrac{{(AB - BP)}}{{AB}} = \dfrac{1}{{\sqrt 2 }}$

$1 - (\dfrac{{BP}}{{AB}}) = \dfrac{1}{{\sqrt 2 }}$

$\dfrac{{BP}}{{AB}} = 1 - \dfrac{1}{{\sqrt 2 }}$

$\dfrac{{BP}}{{AB}} = \dfrac{{2 - \sqrt 2 }}{2}$

6. In the given triangle PQR, LM is parallel to QR and PM: MR = 3: 4. Calculate the value of ratio:

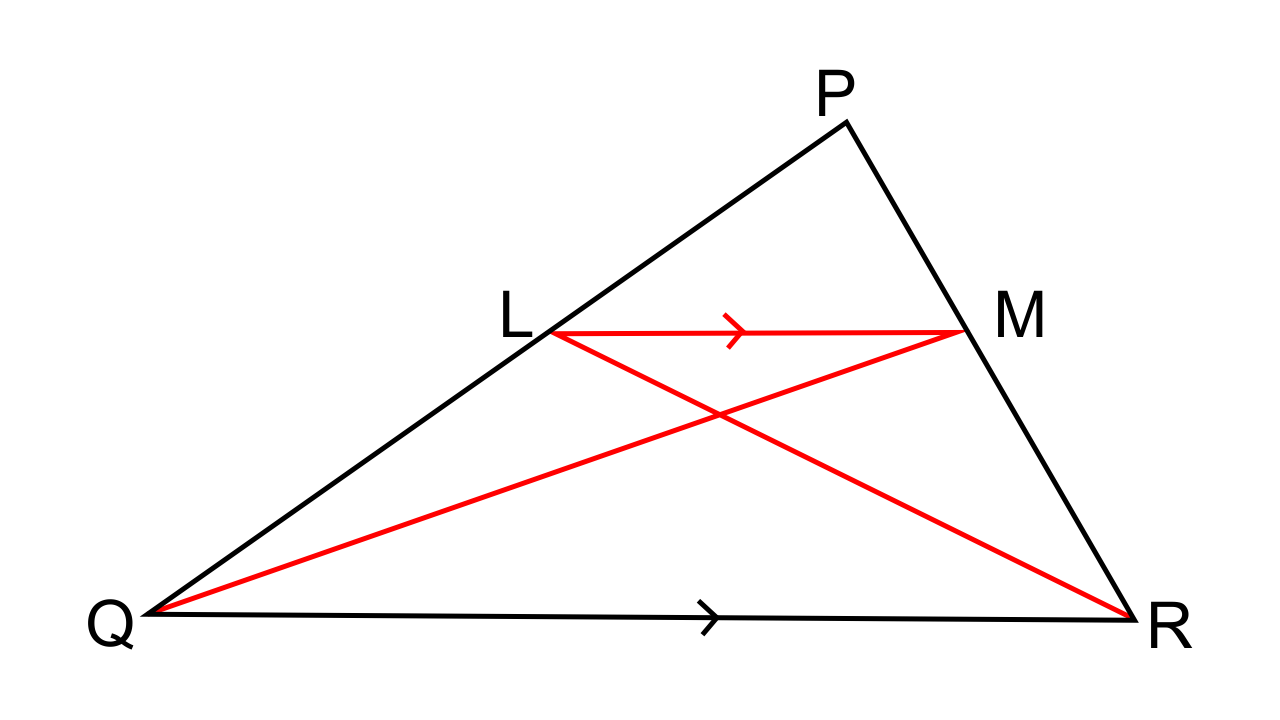
(i) PL/PQ and then LM/QR

(ii) Area of Δ LMN/ Area of Δ MNR

(iii) Area of Δ LQM/ Area of Δ LQN

Ans: (i)Let us consider the Δ PLM and Δ PQR,

As it is mentioned that LM || QR, hence the corresponding points are equal 

∠PLM = ∠PQR

∠PML = ∠PRQ

Hence by AA criterion for similarity, we can say that ∆PLM ~ ∆PQR.

Now we have, 

$\dfrac{{PM}}{{PR}} = \dfrac{{LM}}{{QR}}$

$\dfrac{3}{7} = \dfrac{{LM}}{{QR}}$

By following the Basic Proportionality theorem, we have

$\dfrac{{PL}}{{LQ}} = \dfrac{{PM}}{{MR}} = \dfrac{3}{4}$

$\dfrac{{LQ}}{{PL}} = \dfrac{4}{3}$

$1 + (\dfrac{{LQ}}{{PL}}) = 1 + \dfrac{4}{3}$

$\dfrac{{(PL + LQ)}}{{PL}} = \dfrac{{(3 + 4)}}{3}$

$\dfrac{{PQ}}{{PL}} = \dfrac{7}{3}$

Hence, $\dfrac{{PL}}{{PQ}} = \dfrac{3}{7}$

(ii) We have to find the $\dfrac{\text{Area of }\Delta LMN}{\text{Area of }\Delta MNR}$

ΔLMR and ΔMNR have the same vertex at M and their bases NR and LN are found to be along the same straight line.

The ratio of the areas of the triangles can be expressed as follows,

$\dfrac{\text{Area of }\Delta LMN}{\text{Area of }\Delta RNQ} =\dfrac{LN}{NR}$

Now by considering the Δ LMN and Δ RNQ we have, 

∠NLM = ∠NRQ

∠LMN = ∠NQR (Alternate angles)

Hence, by AA criterion for similarity, we can say that ∆LNM ~ ∆RNQ

Thus now, 

$\dfrac{{MN}}{{QN}} = \dfrac{{LN}}{{NR}} = \dfrac{{LM}}{{QR}} = \dfrac{3}{7}$

∴ $\dfrac{\text{Area of }\Delta LMN}{\text{Area of }\Delta RNQ} = \dfrac{{LN}}{{NR}} = \dfrac{3}{7}$

(iii) We have find Area of Δ LQM/ Area of Δ LQN

As it is mentioned that Δ LQM and Δ LQN have common vertices at L and their bases QM and QN are along the straight line. 

Area of Δ LQM/ Area of Δ LQN =$\dfrac{{QM}}{{QN}} = \dfrac{{10}}{7}$

7.The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate-

(i) the length of AP

(ii) the ratio of the areas of triangle APQ and triangle ABC.

Ans: As it is given in the triangle that the triangles are similar

∆APQ ~ ∆ABC

$\dfrac{{AQ}}{{AC}} = \dfrac{{AP}}{{BC}}$

$ \Rightarrow \dfrac{3}{{AP + PC}} = \dfrac{{AP}}{{15}}$

AP(AP+4)=45 

Let us consider AP = x, then we have 

x(x+4) = 45 

x² + 4x – 45 = 0, on solving this we have 

$ \Rightarrow $ (x + 9) (x – 5 = 0)

x= -9 is not possible and hence 

Value of x = 5 

∴Now AC = AP+PC = 5+4 = 9.

8.In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP: PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm². Calculate

(i) area of triangle CDP

(ii) area of parallelogram ABCD

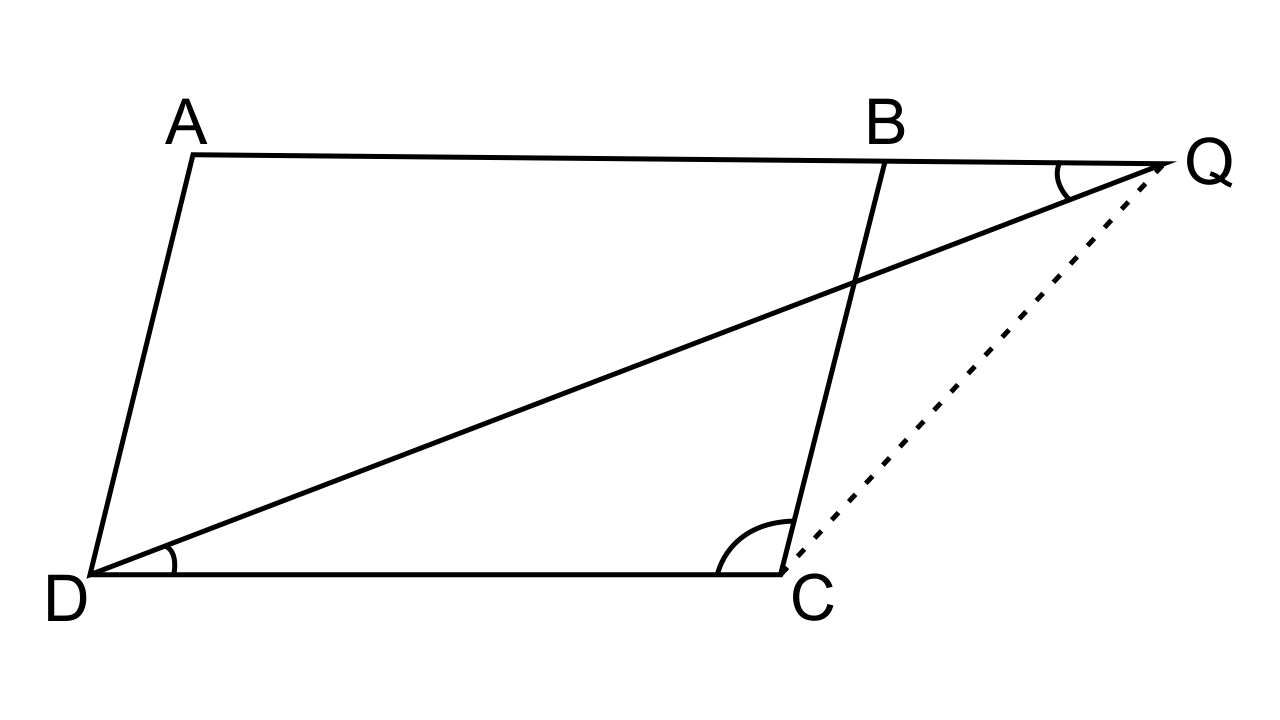
Ans:  (i) To find the area of triangle CDP

 Let us consider ΔBPQ and ΔCPD,

∠DPC = ∠BPQ (As they are vertically opposite angles)

∠PDC = ∠BQP(Alternate angles)

Hence by AA postulates, we can say that ΔBPQ ~ ΔCDP 

∴$\dfrac{{Area{\text{ of }}\Delta {\text{BPQ}}}}{{Area{\text{ of }}\Delta {\text{CPD}}}} = \dfrac{{(B{P^2})}}{{(C{P^2})}} = \dfrac{1}{4}$….. (i)

⇒Area ΔCDP = 4 (Area ΔBPQ)

⇒ 2 (2 Area ΔBPQ) = 2 x 20 = 40 cm² 

(ii) To find the area of parallelogram ABCD

Area of parallelogram ABCD = Area ΔCPD + Area ΔADQ – Area ΔBPQ

Area of parallelogram ABCD = 40 + 9 (area BPQ) – area BPQ

= 40 + 8 (area ΔBPQ)

= 40 + 8 (10) cm²

= 40 + 80

Area of parallelogram ABCD= 120 cm²

9.In the given figure. BC is parallel to DE. Area of triangle ABC = 25 cm². Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC. Also, Find the area of triangle BCD.

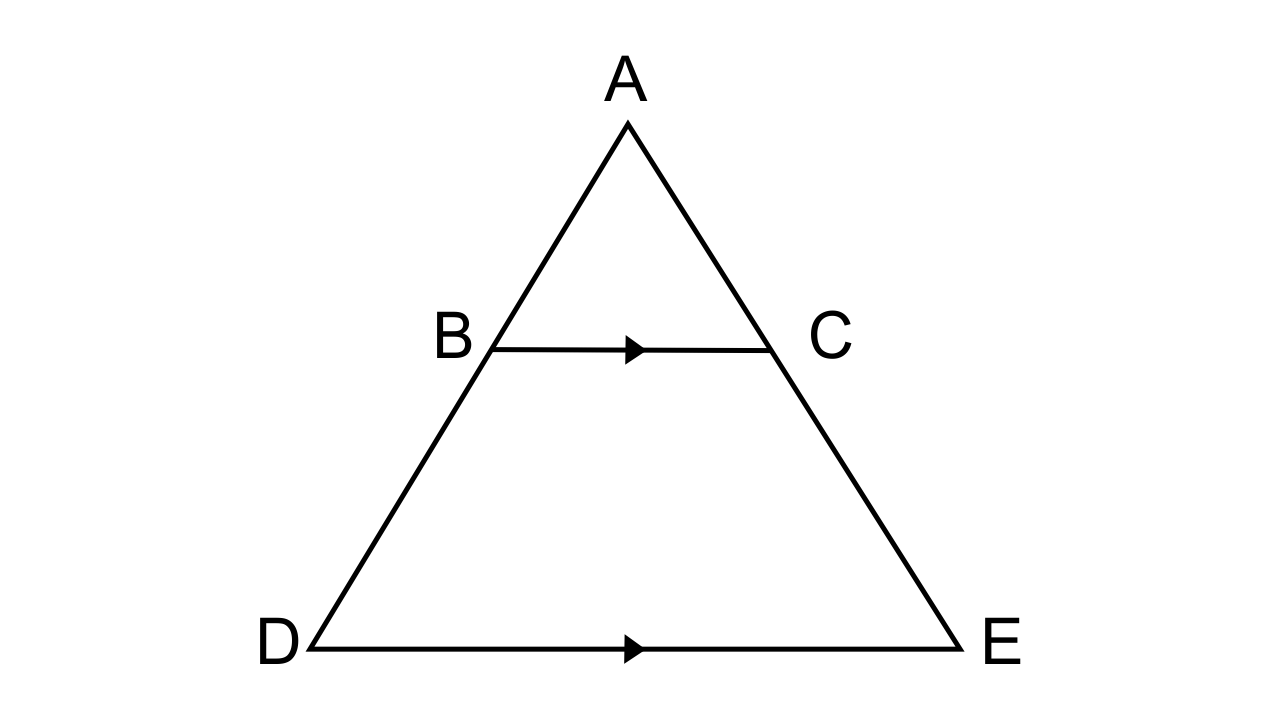
Ans:  It is given that, in ΔADE, BC || DE

Area of ΔABC = 25 cm²

and area of trapezium BCED = 24 cm²

Area of ΔADE = Area of ΔABC + Area of trapezium BCED

Area of ΔADE = 25 + 24 = 49 cm², DE = 14 cm. 

Now let BC = x cm. 

Let us consider ΔABC and ΔADE. 

∠ABC = ∠ADE(corresponding angles)

Hence by AA postulates, we can say that ΔABC ~ ΔADE

∴$\dfrac{{Area{\text{ of }}\Delta A{\text{BC}}}}{{Area{\text{ of }}\Delta ADE}} = \dfrac{{(B{C^2})}}{{(D{E^2})}} = \dfrac{{25}}{{49}} = \dfrac{{B{C^2}}}{{{{(14)}^2}}}$

$ \Rightarrow B{C^2} = 100$

BC = 10cm. 

Let us consider the trapezium BCED, 

Area of trapezium BCED = ½ (Sum of parallel sides) ×h

But we know that area of trapezium BCED = 24 cm² and DE = 14 cm

h =$\dfrac{{Area \times 2}}{{(BC + DE)}} = \dfrac{{48}}{{24}}$ = 2cm.

Now, the Area of ΔBCD= $\dfrac{1}{2} \times 10 \times 2 = 10c{m^2}$

10.The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.

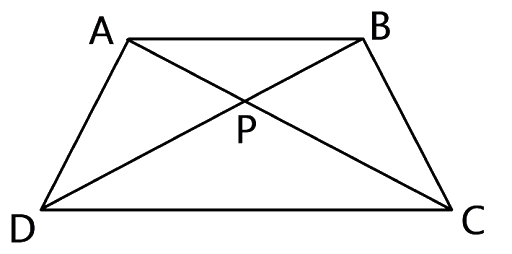
Find-

(i) ΔAPB : ΔCPB

(ii) ΔDPC : ΔAPB

(iii) ΔADP : ΔAPB

(iv) ΔAPB : ΔADB

Ans: It is given that AP : CP = 3 : 5 ⇒\[\dfrac{{AD}}{{DG}} = \dfrac{{CF}}{{FG}}\]

(i) Now let us consider ΔAPB and ΔCPB,

Both of these triangles have the same vertex and their bases are in the same straight lines and hence 

Area ΔAPB : area ΔCPB = AP : PC = 3 : 5  or 

ΔAPB : ΔCPB = 3 : 5

(ii)Now let us consider   ΔAPB and ΔDPC,

∠APB = ∠DPC (As they are vertically opposite angles)

∠PAB = ∠PCD (alternate angles)

Hence by AA postulates, we can say that ΔAPB ~ ΔDPC.

∴\[\dfrac{{Area{\text{ of }}\Delta {\text{DPC}}}}{{Area{\text{ of }}\Delta APB}} = \dfrac{{C{P^2}}}{{A{P^2}}} = \dfrac{{25}}{9}\]

⇒ Area ΔDPC : Area ΔAPB = 25 : 9 or 

⇒ΔDPC : ΔAPB = 25 : 9

(iii) Now let us consider ΔADP and ΔAPB, 

As both of the triangles have the same vertex and their bases arc in the same straight line, we can say that 

Area ΔADP : Area ΔAPB = DP : PB

But PC : AP = 5 : 3

ΔADP : ΔAPB = 5 : 3

(iv) The ΔADB and ΔAPB have same vertex at A and their bases BP 

and BD are along the same parallel line.

Therefore, the ratio of area of triangles is equal to the ratio of 

corresponding sides.

∴ Area of ΔADB/ Area of ΔAPB =\[\dfrac{{PB}}{{BD}}\]PB/ BD = \[\dfrac{3}{8}\].

11.In the given figure, ARC is a triangle. DE is parallel to BC and AD/DB = 3/2.

(i) Determine the ratios AD/AB, DE/BC

(ii) Prove that ΔDEF is similar to ΔCBF.

Hence, find EF/FB

(iii) What is the ratio of the areas of ΔDEF and ΔBFC?

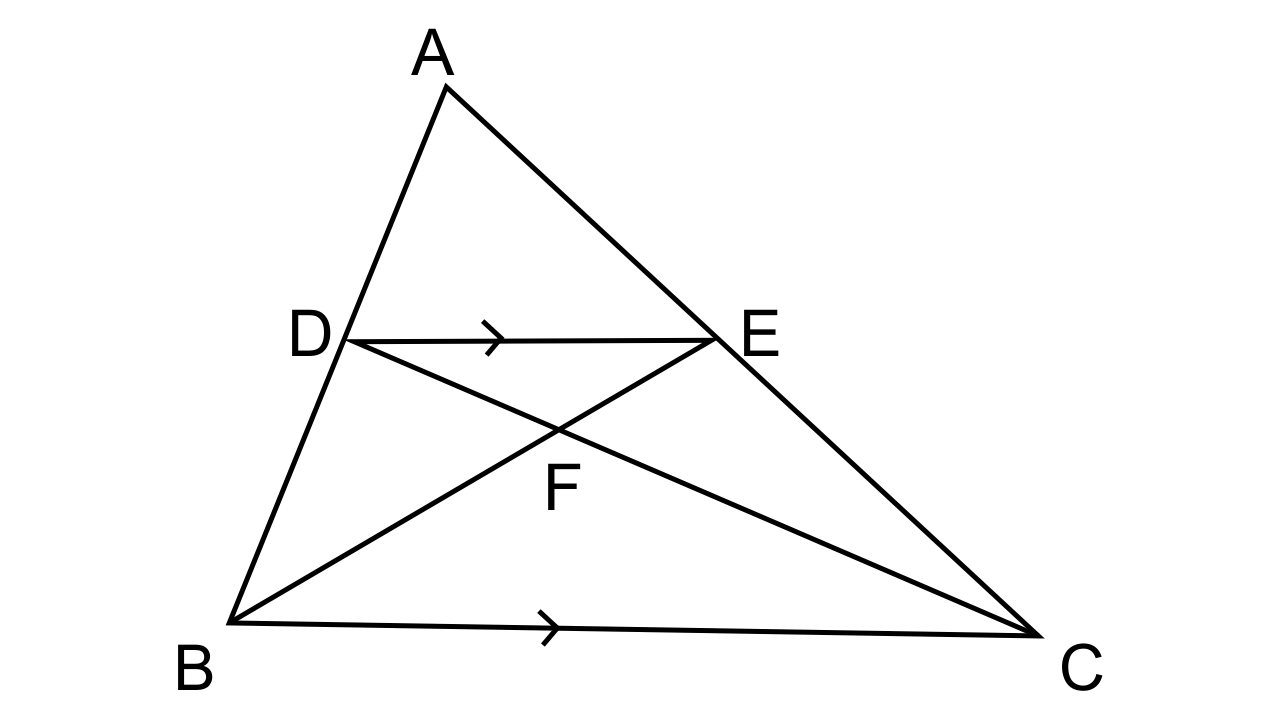
Ans:  It is given that 

ABC is a triangle, DE is parallel to BC and the ratio of AD and DB is 3:2. 

(i) \[\dfrac{{AD}}{{DB}} = \dfrac{3}{2}\]

\[\dfrac{{DB}}{{AD}} = \dfrac{2}{3}\]or

\[\dfrac{{DB}}{{AD}} + 1 = \dfrac{2}{3} + 1\]or it could be also written as 

\[\dfrac{{AB}}{{AD}} = \dfrac{5}{3}\]or

\[\dfrac{{AD}}{{AB}} = \dfrac{3}{5}\]

Now let us consider ΔADE and ΔABC 

∠ADE = ∠B (corresponding angles)

∠AED = ∠C (corresponding angles)

Hence by AA similarity, we can say that ΔADE ~ ΔABC

\[\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\]

∴\[\dfrac{{DE}}{{BC}} = \dfrac{3}{5}\]

(ii)We have to prove that ΔDEF is similar to ΔCBF.

In ∆ DEF and ∆CBF

∠FDE= ∠FCB (Alternate angles) 

∠DFE =∠BFC (Vertical opposite angles)

Hence by AA similarity, we can say that ∆ DEF~ ∆CBF

The ratios of corresponding sides are equal.

\[\dfrac{{EF}}{{FB}} = \dfrac{{DE}}{{BC}}\]

\[\dfrac{{EF}}{{FB}} = \dfrac{3}{5}\]

(iii) The ΔDFE and ΔCBF are similar. Therefore, areas of two similar 

triangles are proportional to the squares of their corresponding sides.

\[\dfrac{{Area{\text{ of }}\Delta {\text{DFE}}}}{{Area{\text{ of }}\Delta {\text{CBF}}}} = \dfrac{{D{E^2}}}{{B{C^2}}} = \dfrac{9}{{25}}\]

12.In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ΔABC and ΔDEC.

Ans: 

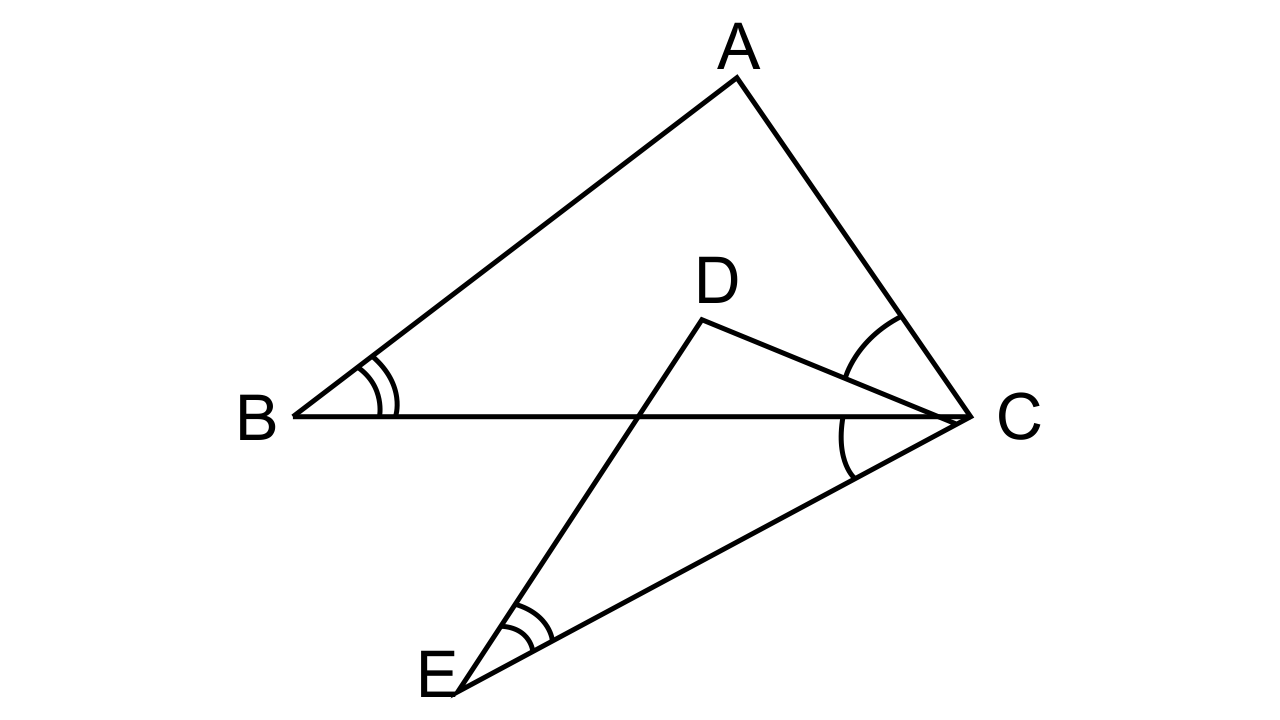
It is given that in the figure DE = 7.8 cm and AB = 10.4 cm. 

∠ACD = ∠ BCE (Given in the question)

Add ∠DCB on both sides,

∠ACD + ∠DCB = ∠DCB + ∠BCE

∠ACB = ∠DCE

Now let us consider ΔABC and ΔDCE

∠B = ∠E(Given in the question)

∠ACB = ∠DCE 

Hence by AA similarity, we can say that ΔABC ~ ΔDCE.

∴\[\dfrac{{Area{\text{ of }}\Delta ABC}}{{Area{\text{ of }}\Delta DCE}} = \dfrac{{A{B^2}}}{{D{E^2}}}\]

As areas of the two similar triangles are in proportional to their corresponding sides 

= \[\dfrac{{A{B^2}}}{{D{E^2}}} = \dfrac{{{{(10.4)}^2}}}{{{{(7.8)}^2}}} = \dfrac{{16}}{9}\]

∴The ratio between areas of the ΔABC and ΔDEC= 16:9.

Exercise 15(D)

1. A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A’ B’ C’ Calculate:

(i) the length of AB, if A’ B’ = 6 cm. 

(ii) the length of C’ A’ if CA = 4 cm.

Ans:   It is given that, triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A’ B’ C’.

(i) It is given that we have to find the length of AB if CA’B’ = 6 cm, 

Now, AB(2.5) = A’B’ = 6 cm

AB = 2.4 cm.

(ii) To find the length of C’ A’ if CA = 4 cm.

We know that, 

CA(2.5) = C’A’

C’A’ = 4 x 2.5 = 10 cm

2. A triangle LMN has been reduced by a scale factor 0.8 to the triangle L’ M’ N’. Calculate:

(i) the length of M’ N’, if MN = 8 cm.

(ii) the length of LM, if L’ M’ = 5.4 cm.

Ans:  It is given that Δ LMN has been reduced by a scale factor m = 0.8 to Δ L’M’N’.

(i) To find the length of M’ N’, if MN = 8 cm.

So, MN (0.8) = M’N’

(8)(0.8) = M’N’

M’N’ = 6.4 cm

(ii) To find the length of LM, if L’ M’ = 5.4 cm.

So, LM (0.8) = L’M’

LM (0.8) = 5.4

LM = 6.75 cm

3. A triangle ABC is enlarged, about the point 0 as centre of enlargement, and the scale factor is 3. Find:

(i) A’B’,if AB = 4 cm.

(ii) BC, if B’C’ = 15 cm.

(iii) OA, if OA’ = 6 cm

(iv) OC’, if OC = 21 cm

Also, state the value of: 

(a) OB’/OB (b) C’A’/CA

Ans:  It has been given that Δ ABC is enlarged and the scale factor m = 3 to the Δ A’B’C’.

(i) To find A’B’, if AB = 4 cm.

So, AB(3) = A’B’

(4)(3) = A’B’

A’B’ = 12 cm

(ii) To find BC if B’C’ = 15 cm

So, BC(3) = B’C’

BC(3) = 15

BC = 5 cm

(iii) To find OA if OA’ = 6 cm

So, OA (3) = OA’

OA (3) = 6

OA = 2 cm

(iv) To find OC’, if OC = 21 cm

Now, OC(3) = OC’

21 × 3 = OC’

OC’ = 63 cm

Also, we have to find the values of OB’/OB and C’A’/CA and as we know the OB’, OB, C’A’, and CA we have.

1. OB’/OB = 3

2. C’A’/CA = 3

4.A model of an aeroplane is made to a scale of 1 : 400. Calculate:

(i) the length, in cm, of the model; if the length of the aeroplane is 40 m.

(ii) the length, in m, of the airplane, if the length of its model is 16 cm.

Ans: It is given that model of an aeroplane to the actual = 1: 400

∴ Scale factor = 400/1

(i) Length of aeroplane = 40 m 

Then the length of model = 40 1/400 = 1/10 m.

= \[\dfrac{1}{{10}} \times 100 = 10cm\]

(ii) The length of aeroplane if the length of the model = 16 cm. 

∴ Length of aeroplane = \[\dfrac{{16 \times 400}}{1}\]= 6400 = 6400/100 = 64 m.

5.The dimensions of the model of a multistorey building are 1.2 m x 75 cm x 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.

Ans: It is been given that the dimensions of a model of multistorey building = 1.2 m × 75 cm × 2 m

Now scale factor is given as = 1: 30 = 1/30

∴ Actual length = 1.2 m × 30 = 36m.

 Breath is given by = 75cm = \[\dfrac{{75 \times 30}}{{100}}m\].

= 2250/100 = 22.5 m

Height = 2m = \[2 \times \dfrac{{30}}{1} = 60m\].

Hence the actual dimensions of the building are 36m × 22.5m × 60m.

6.On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.

Calculate:

(i) the actual lengths of AB and BC in km.

(ii) the area of the plot in sq. km.

Ans: It is given that scale of a map drawn of a triangular plot = 1: 2,50,000 and also the measurement of plot AB = 3 cm, BC = 4 cm and and∠ABC = 90°

Now let us consider the right-angled triangle ABC, 

(i) We have to calculate the actual lengths of AB and BC in km.

The actual length of AB = \[3 \times 25000cm = \dfrac{{3 \times 250000}}{{100000}}km\]

= 15/2 = 7.5 km

Now the actual length of BC = \[\dfrac{{4 \times 250000}}{{100 \times 1000}}\]= 10 km. 

(ii) Area of the plot = ½ × BC × AB.

= \[\dfrac{1}{2} \times 7.5 \times 10k{m^2}\]

= 37.5 km²

7. A model of a ship of made to a scale 1 : 300

(i) The length of the model of ship is 2 m. Calculate the lengths of the ship.

(ii) The area of the deck ship is 180,000 m². Calculate the area of the deck of the model.

(iii) The volume of the model is 6.5 m3. Calculate the volume of the ship. (2016)

Ans: It is given that the model of a ship of made to a scale 1: 300

Now, 

(i) Scale factor k = 1/300

Length of the model = k (Length of the ship)

2 = 1/300 length of the ship.

Length of the ship= 600 m.

(ii) Area of the deck of the model = k²which is equal to the area of the deck of the ship.

Area of the deck of the model = \[{(\dfrac{1}{{300}})^2} \times (180000) = 2{m^2}\]

(iii) The volume of the model = k³ which is the volume of the ship

6.5 = (1/300)³ × Volume of the ship

Volume of the ship = 6.5 × 27000000

Volume of the ship = 175500000 m³

Exercise 15(E)

1.In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

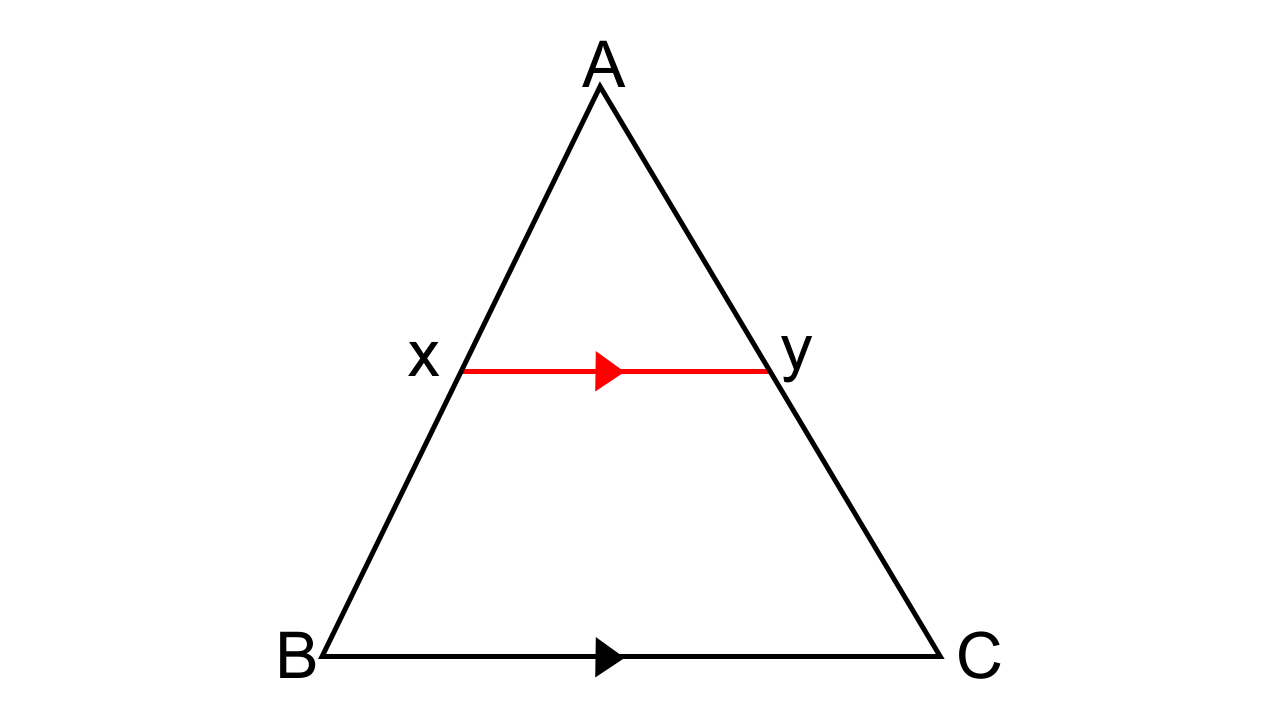
Find:

(i) AY/YC (ii) YC/AC (iii) XY

Ans: It is given that, XY || BC and AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Now let us consider Δ AXY and Δ ABC\

∠AXY = ∠ABC (Corresponding angles are equal)

∠AYX = ∠ACB (Corresponding angles are equal)

Hence by AA criterion for similarity we can say that ∆AXY ~ ∆ABC.

As we have now established that the corresponding sides of the similar triangles are proportional to each other we have, 

(i) \[\dfrac{{AX}}{{AB}} = \dfrac{{AY}}{{AC}}\]

\[\dfrac{9}{{13.5}} = \dfrac{{AY}}{{AC}}\]

\[\dfrac{{AY}}{{YC}} = \dfrac{9}{{4.5}}\]

\[\dfrac{{AY}}{{YC}} = \dfrac{2}{1}\]

\[\dfrac{{AY}}{{YC}} = \dfrac{2}{1}\]

(ii)  To find YC/AC, 

Now we have, 

\[\dfrac{{AX}}{{AB}} = \dfrac{{AY}}{{AC}}\]

\[\dfrac{9}{{13.5}} = \dfrac{{AY}}{{AC}}\]

\[\dfrac{{YC}}{{AC}} = \dfrac{{4.5}}{{13.5}} = \dfrac{1}{3}\]

(iii) To find XY

As we know that ∆AXY ~ ∆ABC

\[\dfrac{{AX}}{{AB}} = \dfrac{{XY}}{{BC}}\]

\[\dfrac{9}{{13.5}} = \dfrac{{XY}}{{18}}\]

XY = \[\dfrac{{(9 \times 18)}}{{13.5}}\]= 12 cm

2. In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF= 13.5 cm, AP = 6 cm and BE = 15 cm,

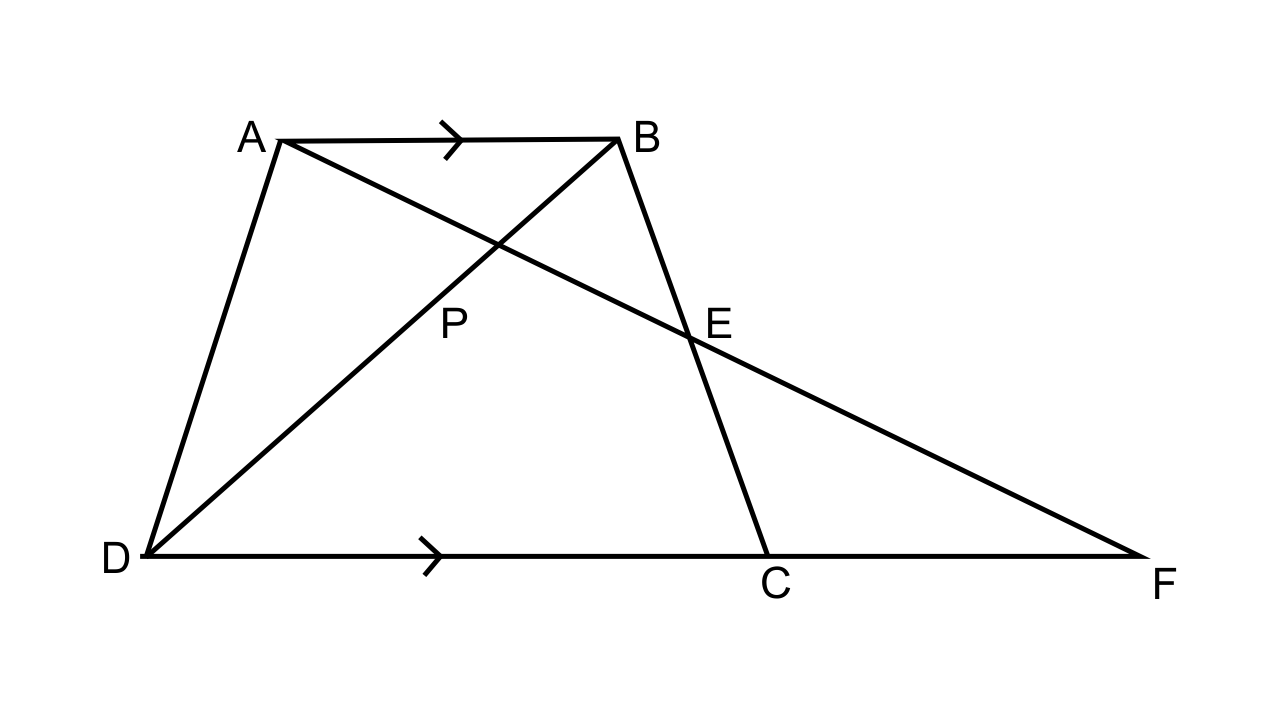
Calculate:

(i) EC 

(ii) AF 

(iii) PE

Ans: (i) Let us consider Δ AEB and Δ FEC,

∠FEC = ∠AEB (Vertically opposite angles)

∠BAE = ∠CFE (As AB||DC)

Hence by considering the AA criterion for similarity we can say that ∆AEB ~ ∆FEC

Now we have, 

\[\dfrac{{AE}}{{FE}} = \dfrac{{BE}}{{EC}} = \dfrac{{AB}}{{FC}}\]

15/EC = 9/13.5

EC = 22.5 cm

(ii) Let us consider the Δ APB and Δ FPD,

∠APB = ∠FPD (Vertically opposite angles)

∠BAP = ∠DFP (Since, AB||DF)

Hence by AA criterion for similarity we can say that ∆APB ~ ∆FPD.

Now we have, 

\[\dfrac{{AP}}{{FP}} = \dfrac{{AB}}{{FD}}\]

\[\dfrac{6}{{FP}} = \dfrac{9}{{31.5}}\]

FP = 21 cm

So, AF = AP + PF = 6 + 21 = 27 cm

(iii) We already have, ∆AEB ~ ∆FEC

So,

AE/FE = BE/CE = AB/FC

AE/FE = 9/13.5

(AF – EF)/ FE = 9/13.5

AF/EF – 1 = 9/13.5

27/EF = 9/13.5 + 1 = 22.5/ 13.5

Therefore, EF = 16.2 cm.

Now, we have 

PE = PF – EF = 21 – 16.2 = 4.8 cm

3.In the following figure, AB, CD and EF are perpendicular to the straight line BDF

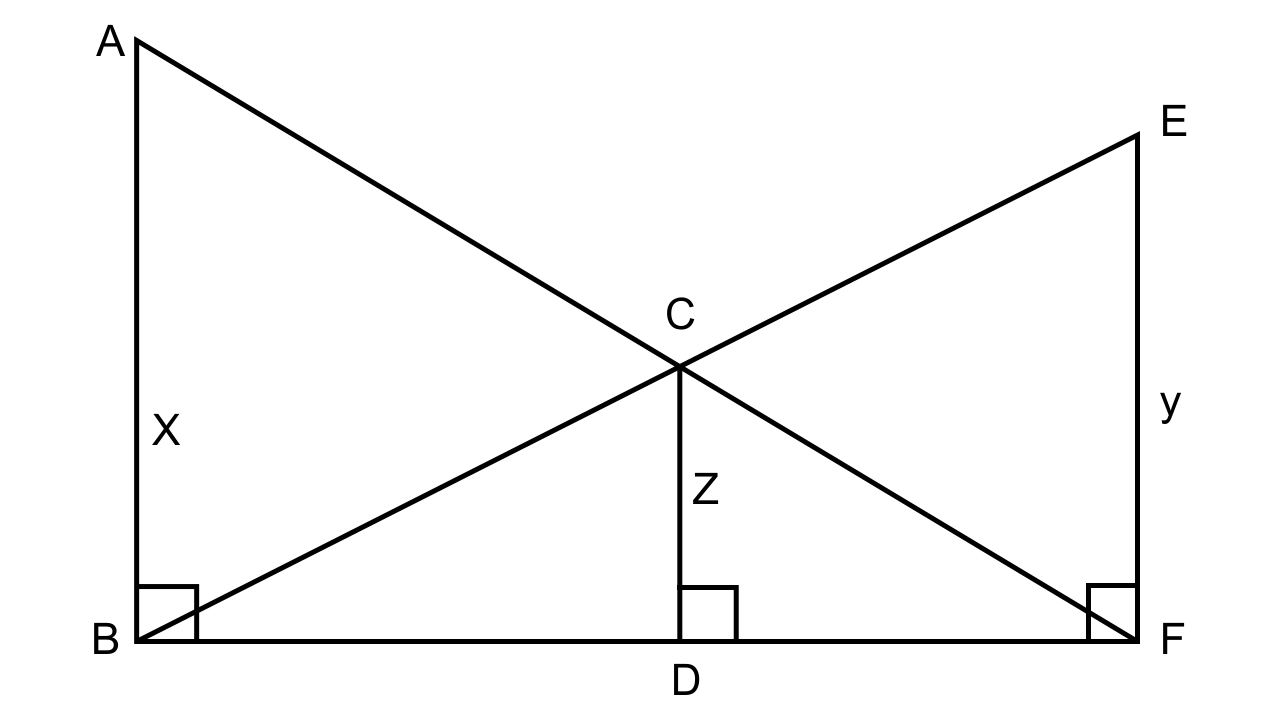
If AB = x and; CD = z unit and EF = y unit, prove that:

\[\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z}\]

Ans: Let us consider Δ FDC and Δ FBA,

∠FDC = ∠FBA (As DC || AB)

∠DFC = ∠BFA (common angle)

Hence by AA criterion for similarity we can say that ∆FDC ~ ∆FBA.

Thus, we have 

DC/AB = DF/BF

\[\dfrac{z}{x} = \dfrac{{DF}}{{BF}}\]…. (1)

Let us consider Δ BDC and Δ BFE,

∠DBC = ∠FBE (Common angle)

∠BDC = ∠BFE [As DC || FE]

Hence by AA criterion for similarity, we can say that ∆BDC ~ ∆BFE.

Now we have, \[\dfrac{{BD}}{{BF}} = \dfrac{z}{y}\]….. (2)

Add (1) and (2), we get

\[\dfrac{{BD}}{{BF}} + \dfrac{{DF}}{{BF}} = \dfrac{z}{y} + \dfrac{z}{x}\]

1 = z/y + z/x, divide both sides by z 

1/z = 1/x + 1/y, hence it is proved.

4.Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that: \[\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}\]

Ans: 

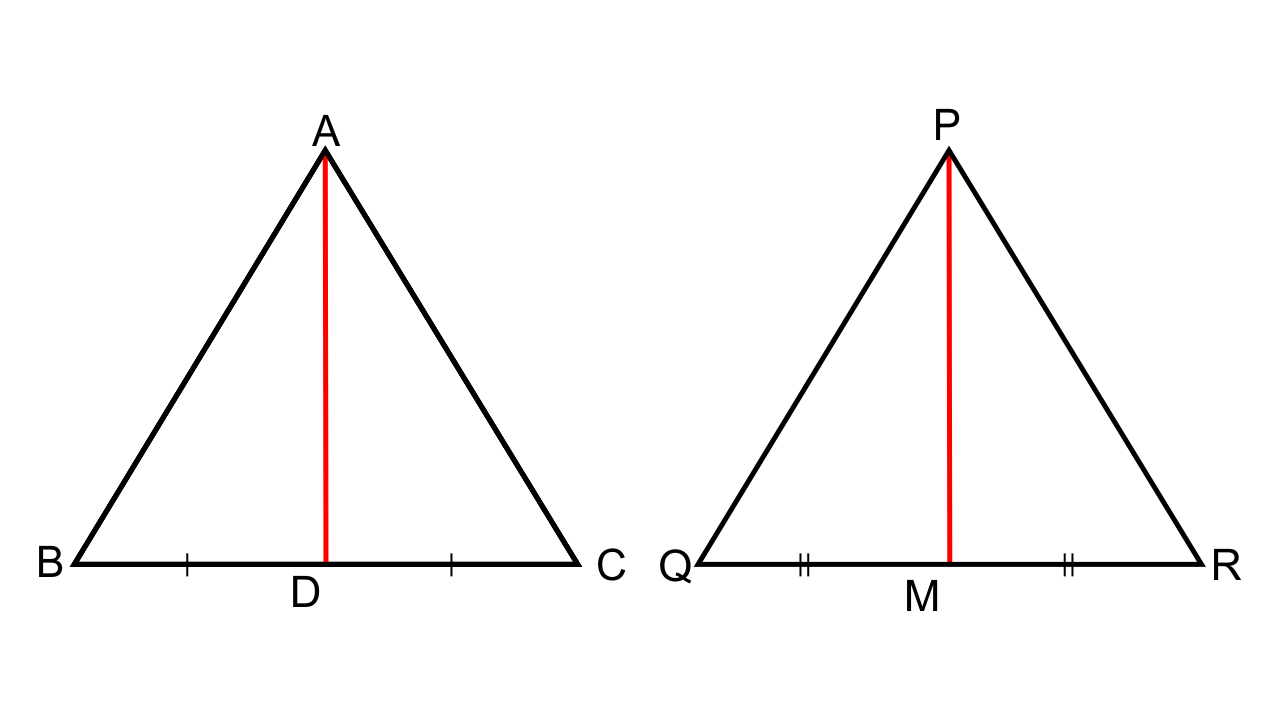
It is given that ∆ABC ~ ∆PQR and AD and PM are the medians, so BD = DC and QM = MR

As the corresponding sides of the similar triangles are proportional we have AB/PQ = BC/QR. 

Now, AB/PQ = (BC/2)/ (QR/2) = BD/QM

and, ∠ABC = ∠PQR i.e. ∠ABD = ∠PQM

Hence by SAS criterion for similarity we can say that ∆ABD ~ ∆PQM 

Therefore, \[\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}\]

5.Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that: \[\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}\]

Ans: 

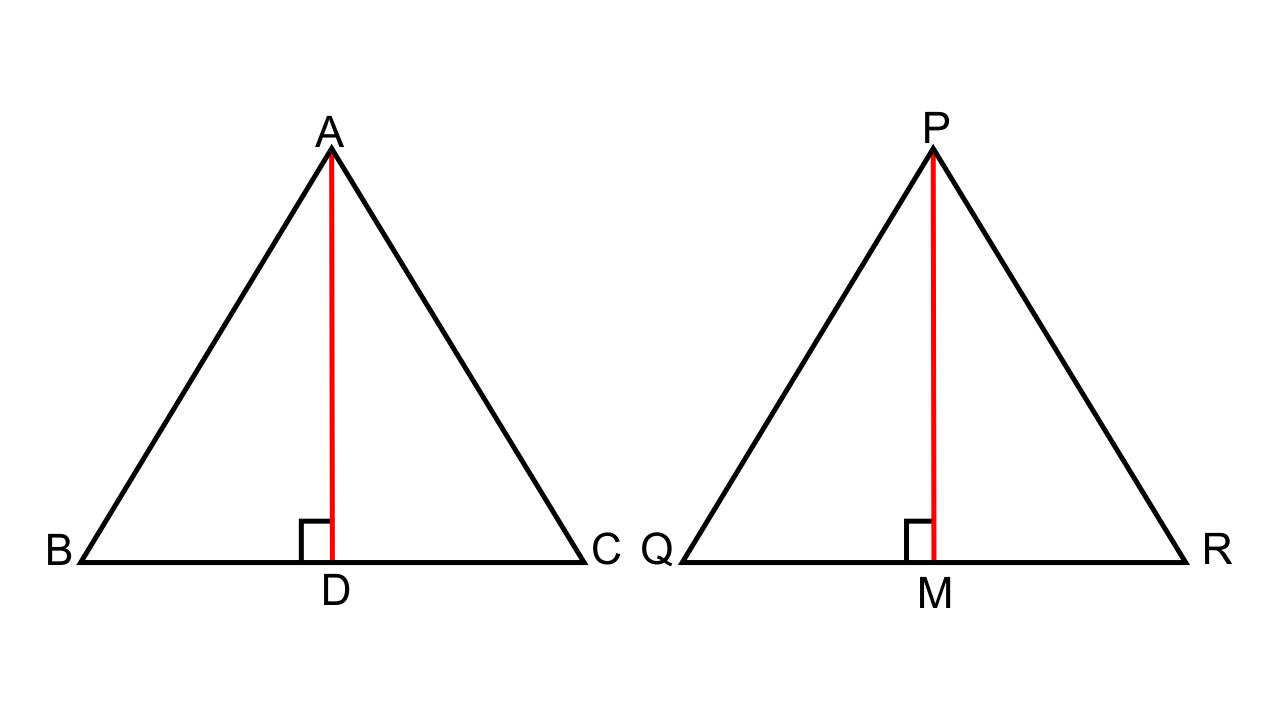
It is given that ∆ABC ~ ∆PQR

Now, ∠ABC = ∠PQR (Corresponding angles)

∠ABD = ∠PQM (Corresponding angles)

∠ADB = ∠PMQ (Both are right angles)

Hence by AA criterion for similarity, we can say that ∆ABD ~ ∆PQM.

Thus, now we can say that, 

\[\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}\]

6.Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and the bisector of angle QPR meets QR at point M, prove that:

\[\mathbf{\dfrac{{AB}}{{PQ}}} = \mathbf{\dfrac{{AD}}{{PM}}}\]

Ans: 

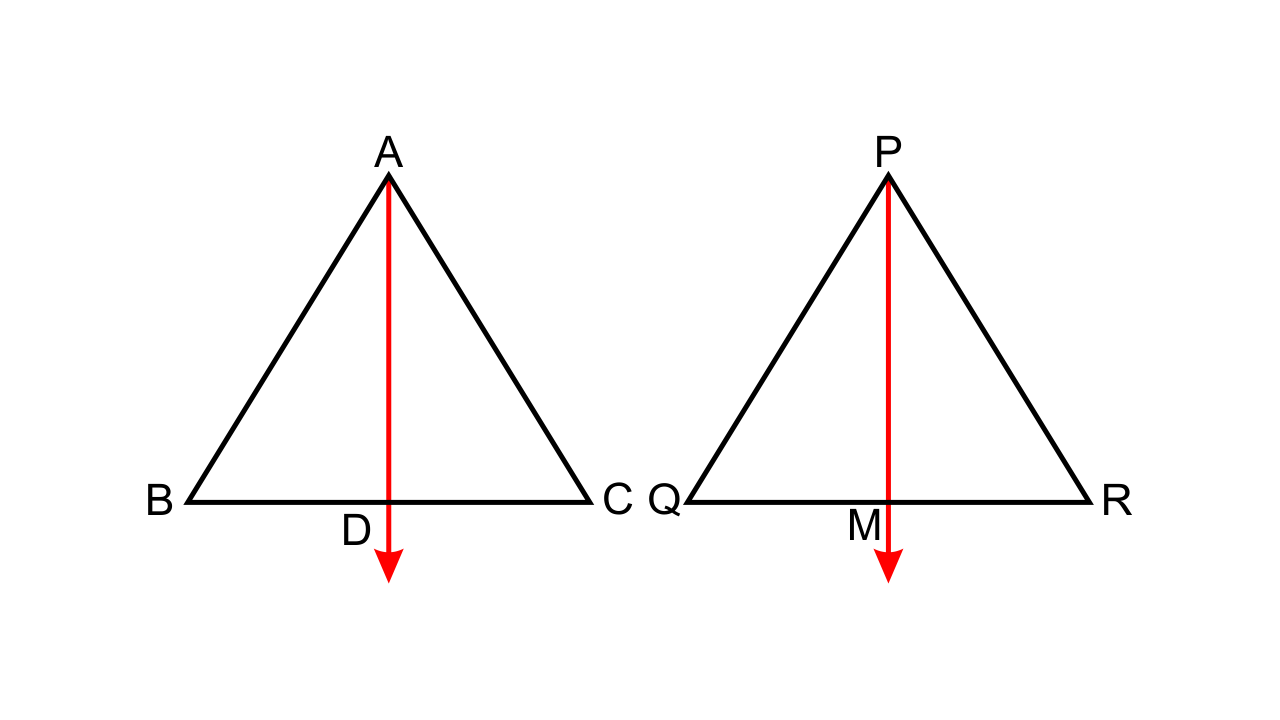
It is given that ∆ABC ~ ∆PQR and AD and PM are the angle bisectors.

So now we have, 

∠BAD = ∠QPM (Both are right angles)

∠ABC = ∠PQR i.e. ∠ABD = ∠PQM

Hence by AA criterion for similarity we can say that ∆ABD ~ ∆PQM. 

Thus, we can say that \[\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}\]

7.In the following figure, ∠AXY = ∠AYX. If BX/AX = CY/AY, show that triangle ABC is isosceles.

Ans: It is given that, ∠AXY = ∠AYX

So now we have AX = AY, as sides opposite to equal angles are equal. 

By considering BPT we have, 

\[\dfrac{{BX}}{{AX}} = \dfrac{{CY}}{{AY}}\]

Hence, AX + BX = AY + CY

As AB = AC, we can say that ∆ABC is an isosceles triangle.

8. In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.

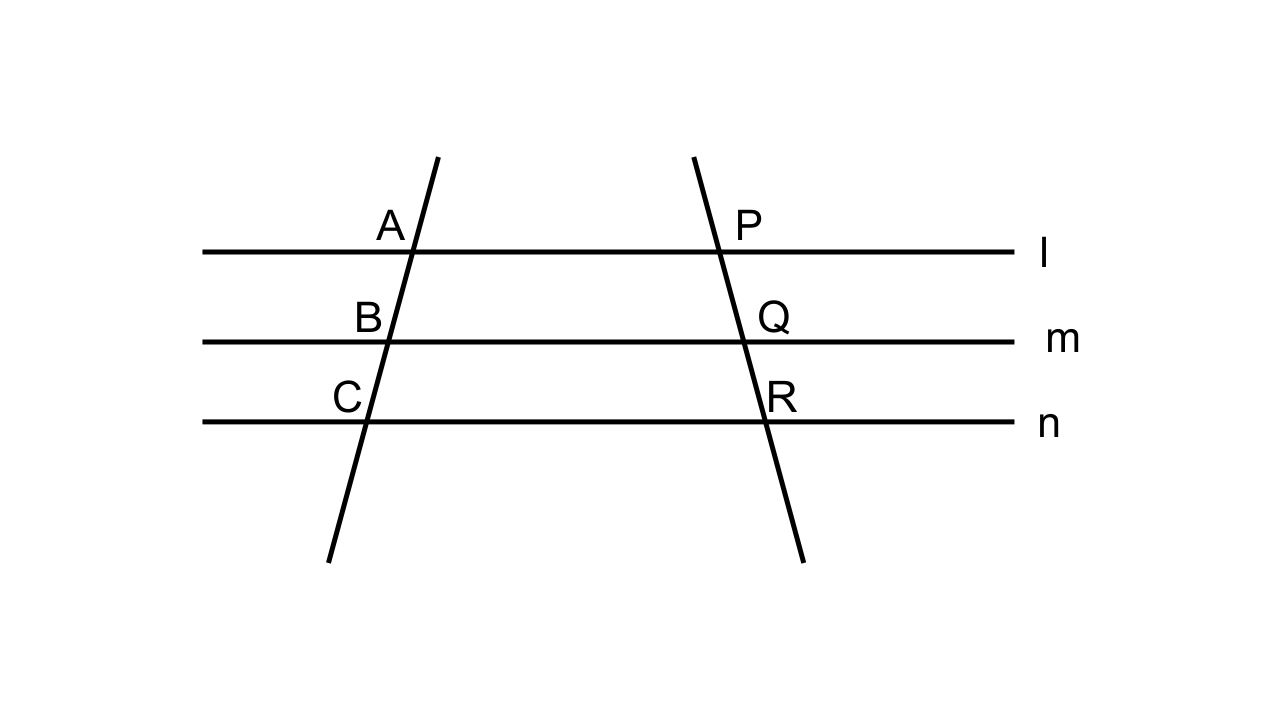
Prove that: \[\mathbf{\dfrac{{AB}}{{BC}} = \dfrac{{PQ}}{{QR}}}\]

Ans: 

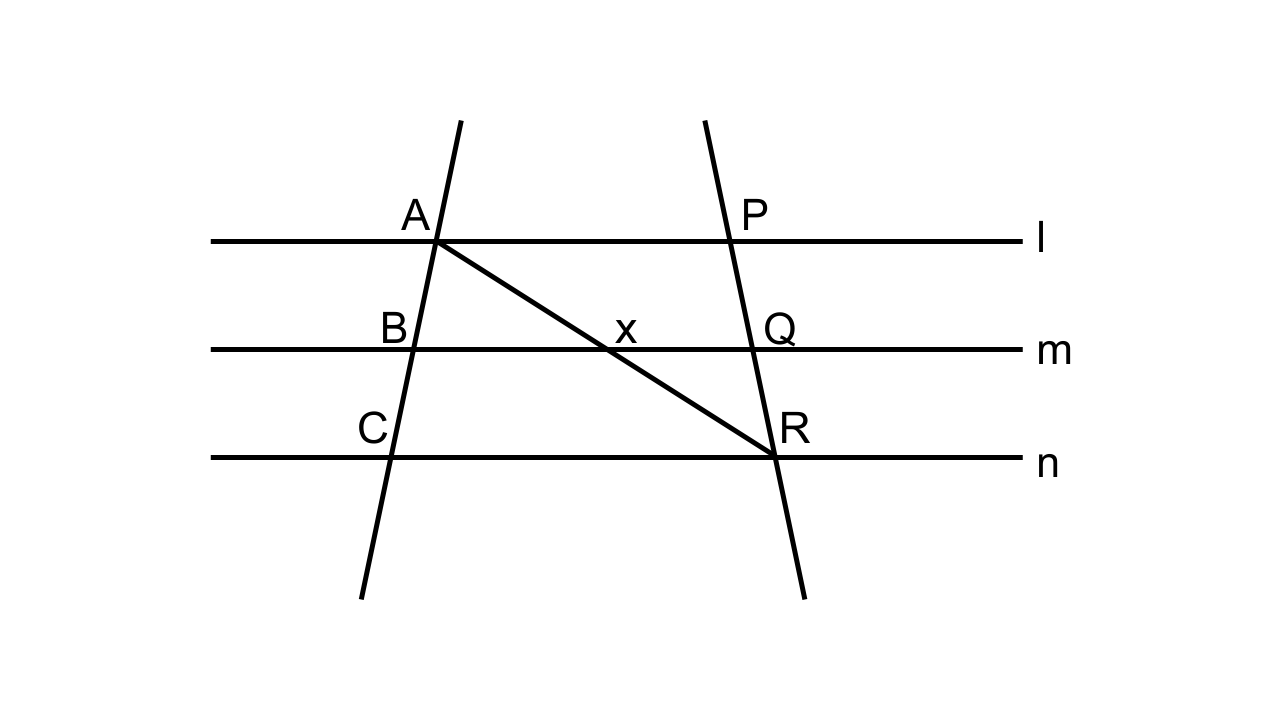
Consider the figure given in the question. Let join AR such that it intersects BQ at point X.

Let us consider ∆ACR were BX || CR.By, BPT we have 

\[\dfrac{{AB}}{{BC}} = \dfrac{{AX}}{{XR}}\]...… (1) 

Let us consider ∆APR were XQ || AP.By BPT we have 

\[\dfrac{{PQ}}{{QR}} = \dfrac{{AX}}{{XR}}\].. … (2)

From (1) and (2),

\[\dfrac{{AB}}{{BC}} = \dfrac{{PQ}}{{QR}}\]

AB/BC = PQ/QR, Hence, it is proved. 

9.In the following figure, DE || AC and DC || AP. Prove that: \[\mathbf{\dfrac{{BE}}{{EC}} = \dfrac{{BC}}{{CP}}}\]

Ans:  

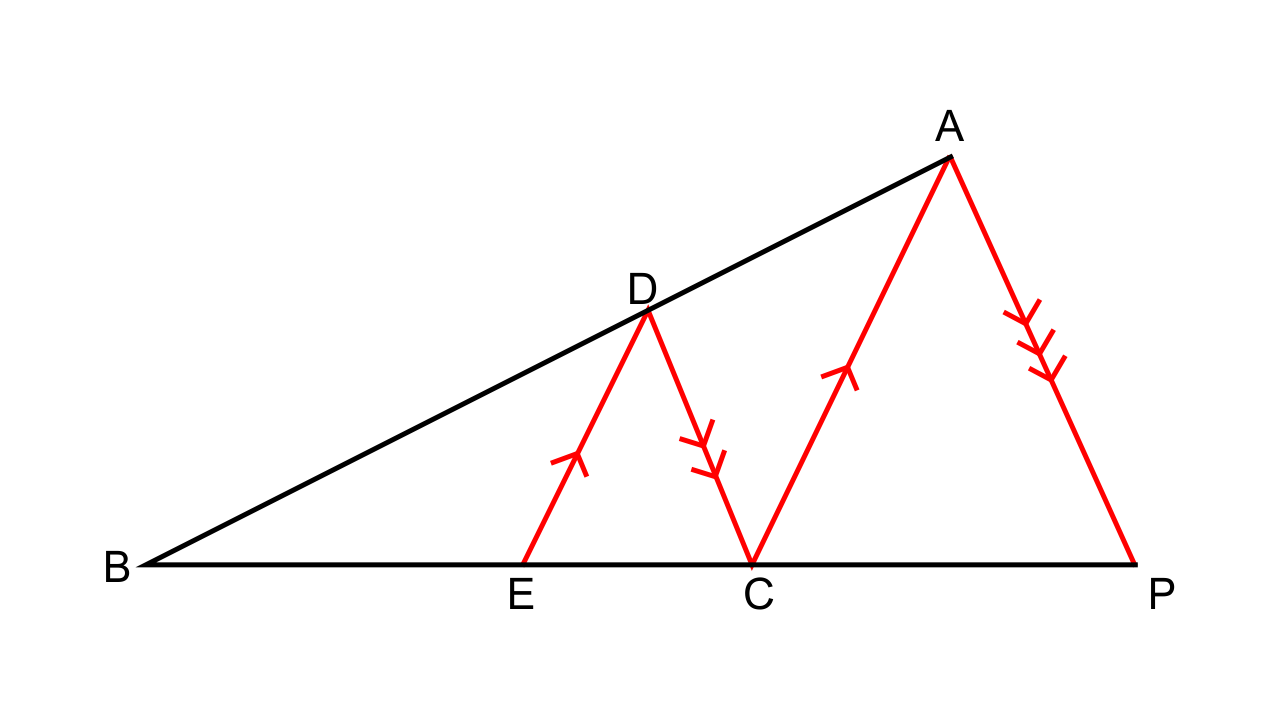
It is given that DE || AC and DC || AP.

So now we have, 

\[\dfrac{{BE}}{{EC}} = \dfrac{{BD}}{{DA}}\](By basic proportionality theorem)

And as DC || AP we will have 

\[\dfrac{{BE}}{{EC}} = \dfrac{{BD}}{{DA}}\](By basic proportionality theorem)

Therefore, \[\dfrac{{BE}}{{EC}} = \dfrac{{BC}}{{CP}}\]

10. In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.

Calculate: 

(i) EF 

(ii) AC

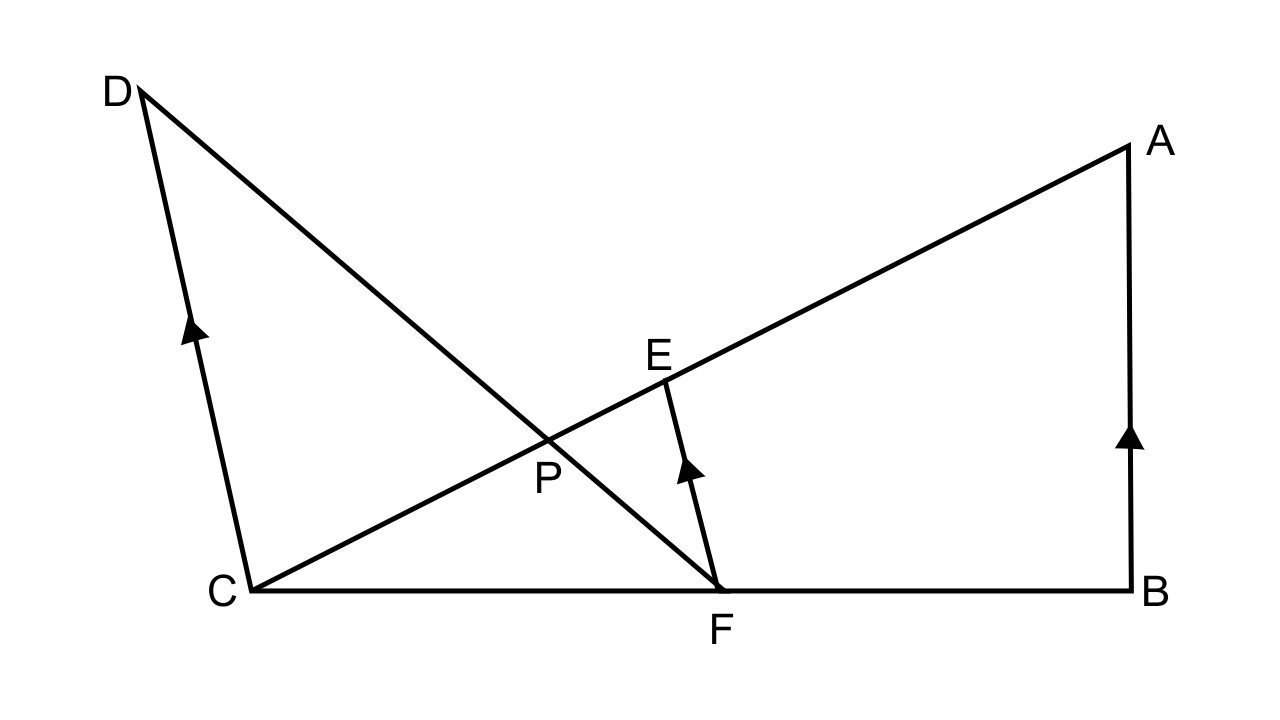
Ans:  (i) It is given that AB ‖ EF ‖ CD and AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.

Let us consider ∆PCD and ∆PEF,

∠CPD = ∠EPF (Vertically opposite angles)

∠DCE = ∠FEP (As DC || EF, alternate angles.)

Hence by considering the AA criterion for similarity we have ∆PCD ~ ∆PEF.

Now we have \[\dfrac{{27}}{{EF}} = \dfrac{{15}}{{7.5}}\]

EF = 13.5 

(ii) As it is been given that EF || AB

We can say that by following the AA criterion for similarity we have ∆CEF ~ ∆CAB.

\[\dfrac{{EC}}{{AC}} = \dfrac{{EF}}{{AB}}\]

\[\dfrac{{22.5}}{{AC}} = \dfrac{{13.5}}{{22.5}}\]

Thus, AC = 37.5 cm

11.In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.

(i) Prove that ΔACD is similar to ΔBCA.

(ii) Find BC and CD

(iii) Find the area of ΔACD: area of ΔABC

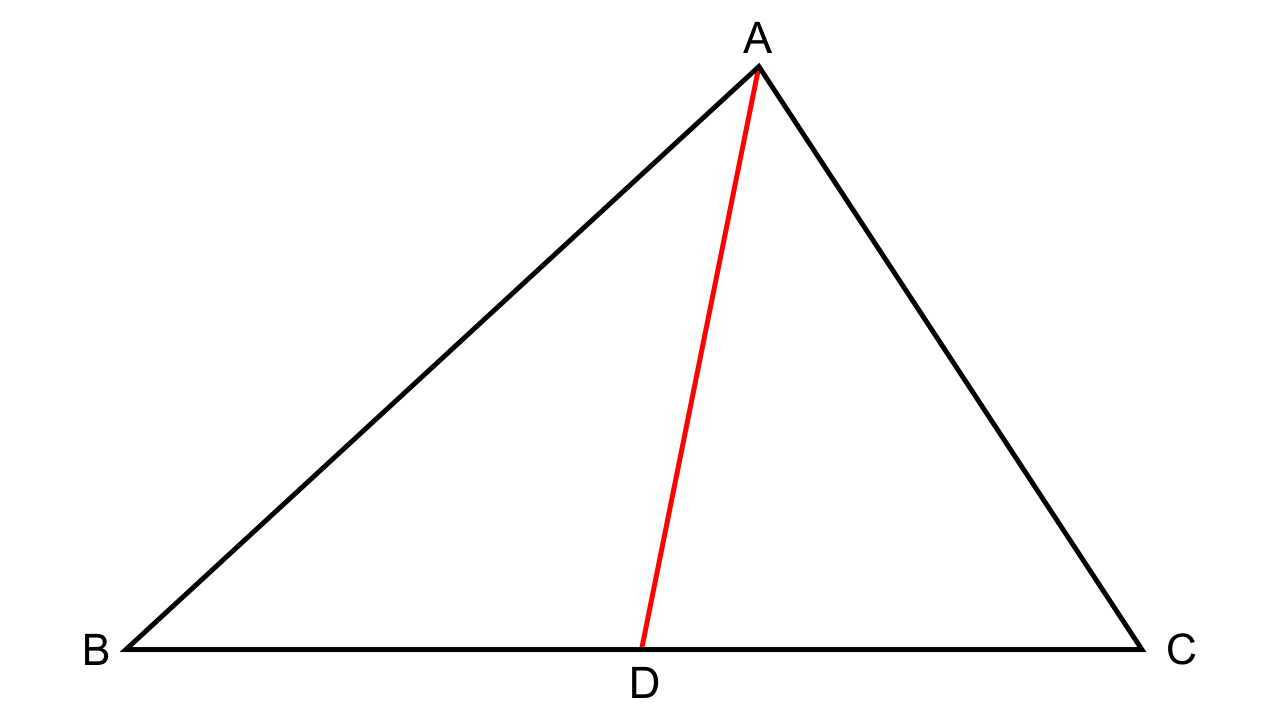
Ans: (i) Let us consider ∆ACD and ∆BCA,

It is given that ∠DAC = ∠ABC

∠ACD = ∠BCA (Common angles)

Hence by AA similarity, we can say that ∆ACD ~ ∆BCA.

(ii)  As we have established that ∆ACD ~ ∆BCA.

We have, 

\[\dfrac{{AC}}{{BC}} = \dfrac{{CD}}{{CA}} = \dfrac{{AD}}{{AB}}\]

\[\dfrac{4}{{BC}} = \dfrac{{CD}}{4} = \dfrac{5}{8}\]

\[\dfrac{4}{{BC}} = \dfrac{5}{8}\]

BC = 6.4 cm, also 

\[\dfrac{{CD}}{4} = \dfrac{5}{8}\]

CD = 2.5 cm 

(iii) As we know that ∆ACD ~ ∆BCA

Now we have, 

\[\dfrac{{Area{\text{ of (}}\Delta {\text{ACD)}}}}{{Area{\text{ of (}}\Delta BCA)}} = \dfrac{{A{D^2}}}{{A{B^2}}} = \dfrac{{{5^2}}}{{{8^2}}} = \dfrac{{25}}{{64}}\]

12.In the given triangle P, Q and R are mid-points of sides AB, BC and AC respectively. Prove that triangle QRP is similar to triangle ABC.

Ans: 

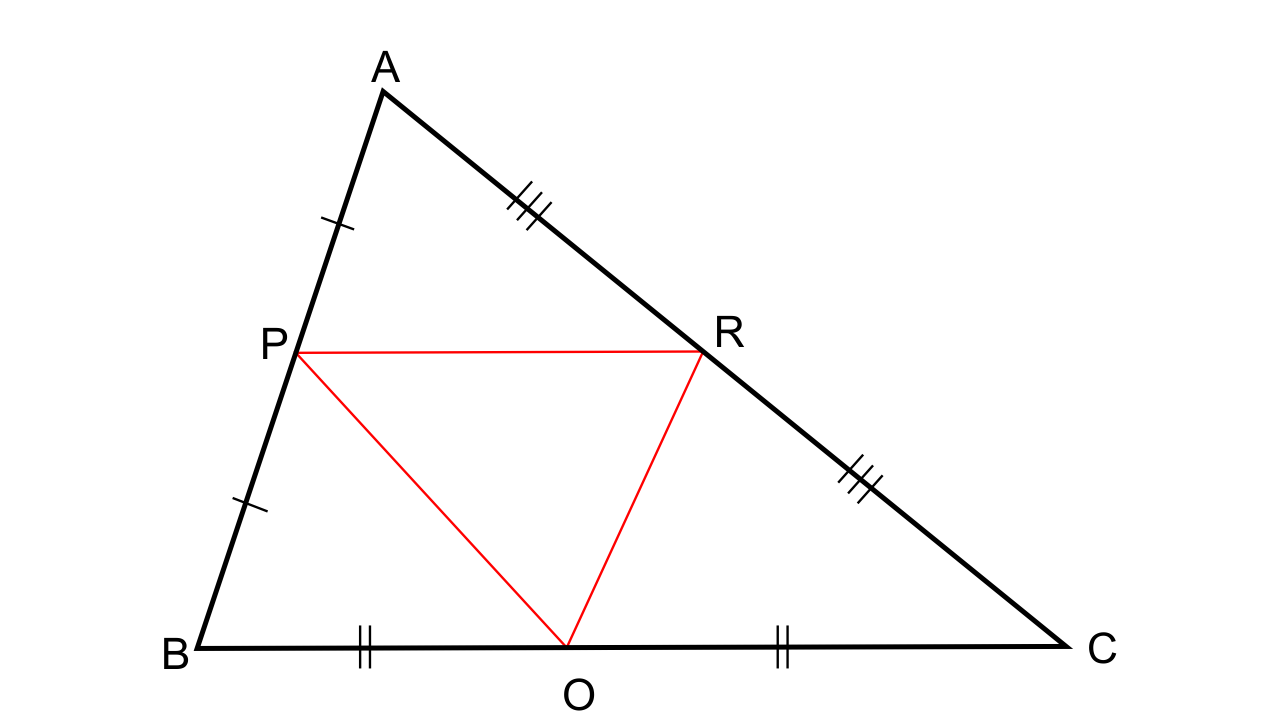
Let us consider ∆ABC and as PR || BC by BPT we have 

\[\dfrac{{AP}}{{PB}} = \dfrac{{AR}}{{RC}}\]

Now let us consider ∆PAR and ∆BAC,

∠PAR = ∠BAC (Common angles)

∠APR = ∠ABC (Corresponding angles)

Hence by AA criteria for similarity, we can say that ∆PAR ~ ∆BAC.

Thus, now we have, 

\[\dfrac{{PR}}{{BC}} = \dfrac{{AP}}{{AB}} = \dfrac{1}{2}\](As P is the midpoint of AB)

PR = ½ BC

Similarly,

PQ = ½ AC

RQ = ½ AB

So,

\[\dfrac{{PR}}{{BC}} = \dfrac{{PQ}}{{AC}} = \dfrac{{RQ}}{{AB}}\]

Therefore,

By SSS similarity we can say that ∆QRP ~ ∆ABC

13.In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:

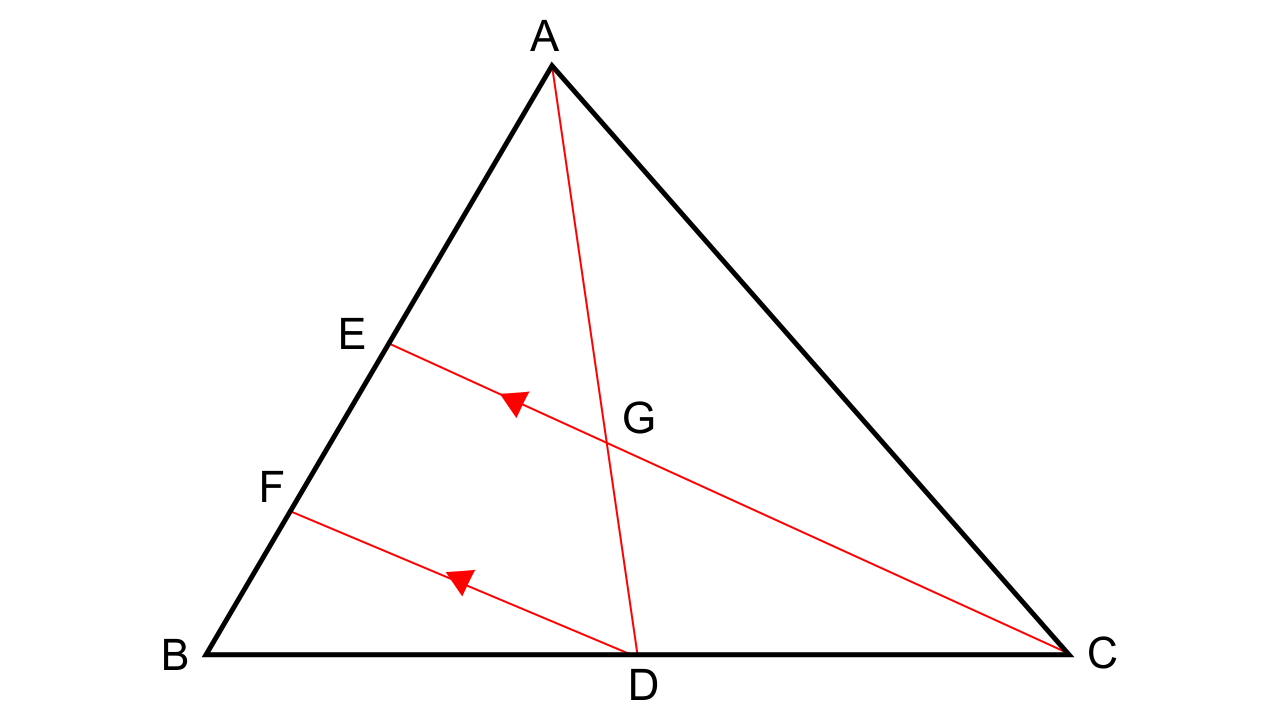
(i) EF = FB,

(ii) AG: GD = 2: 1

Ans: (i) Let us consider ∆BFD and ∆BEC,

∠BFD = ∠BEC (Corresponding angles)

∠FBD = ∠EBC (Common angles)

Hence by AA criteria for similarity, we can say that ∆BFD ~ ∆BEC.

\[\dfrac{{BF}}{{BE}} = \dfrac{{BD}}{{BC}}\]

\[\dfrac{{BF}}{{BE}} = \dfrac{1}{2}\] (As D is the midpoint of BC)

BE = 2BF

BF = FE = 2BF

Thus,

EF = FB

(ii) Let us consider ∆AFD in which EG || FD. Now by using BPT we have 

\[\dfrac{{AE}}{{EF}} = \dfrac{{AG}}{{GD}}\]…. (1)

Now as AE = EB (As E is the midpoint of AB)

AE = 2EF

From equation 1 we have 

\[\dfrac{{AG}}{{GD}} = \dfrac{2}{1}\]

Therefore, AG: GD = 2: 1

14.Two similar triangles are equal in area. Prove that the triangles are congruent.

Ans:  As it is given that two similar triangles are equal, let us consider that ∆ABC ~ ∆PQR.

So now we have,

\[\dfrac{{Area{\text{ of (}}\Delta {\text{ABC)}}}}{{Area{\text{ of (}}\Delta PQR)}} = {(\dfrac{{AB}}{{PQ}})^2} = {(\dfrac{{BC}}{{QR}})^2} = {(\dfrac{{AC}}{{PR}})^2}\]

Since it is given that, Area of ∆ABC = Area of ∆PQR, hence 

AB = PQ

BC = QR

AC = PR

As we know that the respective sides of the two similar triangles are all of the same length, we can conclude that.

∆ABC ≅ ∆PQR (By SSS rule)

Hence it is proved. 

15. The ratio between the altitudes of two similar triangles is 3: 5; write the ratio between their:

(i) Medians. 

(ii) Perimeters. 

(iii) Areas.

Ans: We know that the ratio between the altitudes of two similar triangles is the same as the ratio between their sides.

So now we have, 

(i)  The ratio between the medians of two similar triangles is the same as the ratio between their sides.

Thus, the required ratio = 3: 5

(ii) The ratio between the perimeters of two similar triangles is the same as the ratio between their sides.

Thus, the required ratio = 3: 5

(iii) The ratio between the areas of two similar triangles is the same as the square of the ratio between their corresponding sides.

Thus, the required ratio = (3)2: (5)2 = 9: 25

16. The ratio between the areas of two similar triangles is 16 : 25. Find the ratio between their:

(i) Perimeters

(ii) Altitudes

(iii) Medians.

Ans: It is given that the ratio between the areas of two similar triangles is 16 : 25.

The ratio between the medians of the two triangles that are similar 

to each other is the same as the ratio of their corresponding sides.

Ratio = \[\sqrt {\dfrac{{16}}{{25}}} \]= 4:5. 

17.The following figure shows a triangle PQR in which XY is parallel to QR. If PX: XQ = 1:3 and QR = 9 cm, find the length of XY.

Further, if the area of ∆ PXY = x cm2; find in terms of x, the area of :

(i) Triangle PQR.

(ii) Trapezium XQRY.

Ans:  Let us consider ∆PXY and ∆ PQR in which XY is parallel to QR so in a way we can say that corresponding angles are equal.

∠PXY = ∠PQR

∠PYX = ∠PRQ 

Hence by AA criteria for similarity, we can say that ∆PXY ~ ∆PQR

\[\dfrac{{PX}}{{PQ}} = \dfrac{{XY}}{{QR}}\]

\[\dfrac{1}{4} = \dfrac{{XY}}{{QR}}\]

\[\dfrac{1}{4} = \dfrac{{XY}}{9}\]

XY = 2.25 cm.

(i) We know that the ratio of the areas of two similar triangles are equal to the ratio of the squares of their corresponding sides. 

\[\dfrac{{Area{\text{ of (}}\Delta {\text{PXY)}}}}{{Area{\text{ of (}}\Delta {\text{PQR)}}}} = {(\dfrac{{PX}}{{PQ}})^2}\]

\[\dfrac{x}{{Area{\text{ of (}}\Delta {\text{PQR)}}}} = \dfrac{1}{{16}}\]

\[Area{\text{ of (}}\Delta {\text{PQR)  =  16 xc}}{{\text{m}}^2}.\]

(ii) Area of trapezium XQRY = Area of ∆PQR - Area of ∆ PXY 

= (16x-x)cm²

= 15x cm²

18.On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm, and BC = 32 cm. Calculate :

(i) The diagonal distance of the plot in kilometer

(ii) The area of the plot in sq. km.

Ans: It is given that the scale = 1:20000

1cm represents 20000 cm = \[\dfrac{{20000}}{{1000 \times 100}}\]= 0.2 km. 

(i) AC² = AB² + BC²

It is given that AB = 24 cm, and BC = 32 cm

AC² = 576+1024 = 1600

AC = 40 cm 

Actual length of the diagonal = 40× 0.2 km = 8 km.

(ii) To find the area of the plot in sq. km.

1 cm represents 0.2 km 

1 cm² represents 0.2 × 0.2 km²

Let us consider the rectangle ABCD = AB × BC = 24 × 32 = 768 cm²

Actual area of the plot = 30.72 km²

19. The dimensions of the model of a multi storeyed building are lm by 60 cm by 1.20 m. If the scale factor is 1 : 50. Find the actualdimensions of the building. Also, find:

(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq cm.

(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90m3

Ans: The dimensions of the building can be calculated by following the below given procedure. 

Length = 50 m 

Breadth = 0.60× 50 m = 30 m

Height =120 × 50 m = 60 m

Hence the actual dimensions of the building are 50m × 30m × 60m

(i) Floor area of the room of the building = \[50 \times {(\dfrac{{50}}{1})^2}\]=125000 cm² = 12.5 m²

(ii) Volume of the model of the building =.

20.In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:

(i) ∆PQL ~ ∆RPM

(ii) QL x RM = PL x PM

(iii) PQ² = QR x QL

Ans: (i) Let us consider ∆PQL and ∆RPM

∠PQL = ∠RPM (Given)

∠LPQ = ∠MRP (Given)

Hence by the AA criterion of similarity, we can say that ∆PQL ~ ∆RPM

(ii) As it has been proved that ∆PQL ~ ∆RPM

∴\[\dfrac{{QL}}{{PM}} = \dfrac{{PL}}{{RM}}\]

QL.RM = PL.PM 

(iii) Now let us consider ∆LQP and ∆PQR

∠Q = ∠Q (Common angle)

∠LPQ = ∠ QRP (Given information)

By AA criterion of similarity, we have ∆LQP ~ ∆PQR

∴\[\dfrac{{PQ}}{{QR}} = \dfrac{{QL}}{{PQ}}\]

PQ² = QR × QL

21.A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ∆DEF such that the longest side of $\Delta \dfrac{{AB}}{{DE}}$DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ∆DEF.

Ans: It is given that triangle ABC is enlarged to DEF, So the two triangles are said to be similar. 

∴\[\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}}\]

Longest side in the ∆ ABC = BC = 6cm 

Corresponding longest side in ∆DEF = EF = 9 cm 

Scale factor = \[\dfrac{{EF}}{{BC}} = \dfrac{3}{2} = 1.5\]

\[\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}} = \dfrac{2}{3}\]

DE = \[\dfrac{3}{2}\]AB = 4.5 cm 

Similarly, DF = \[\dfrac{3}{2}\]AC= 6 cm. 

22.Two isosceles triangles have equal vertical angles. Show that the triangles are similar.If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.

Ans: 

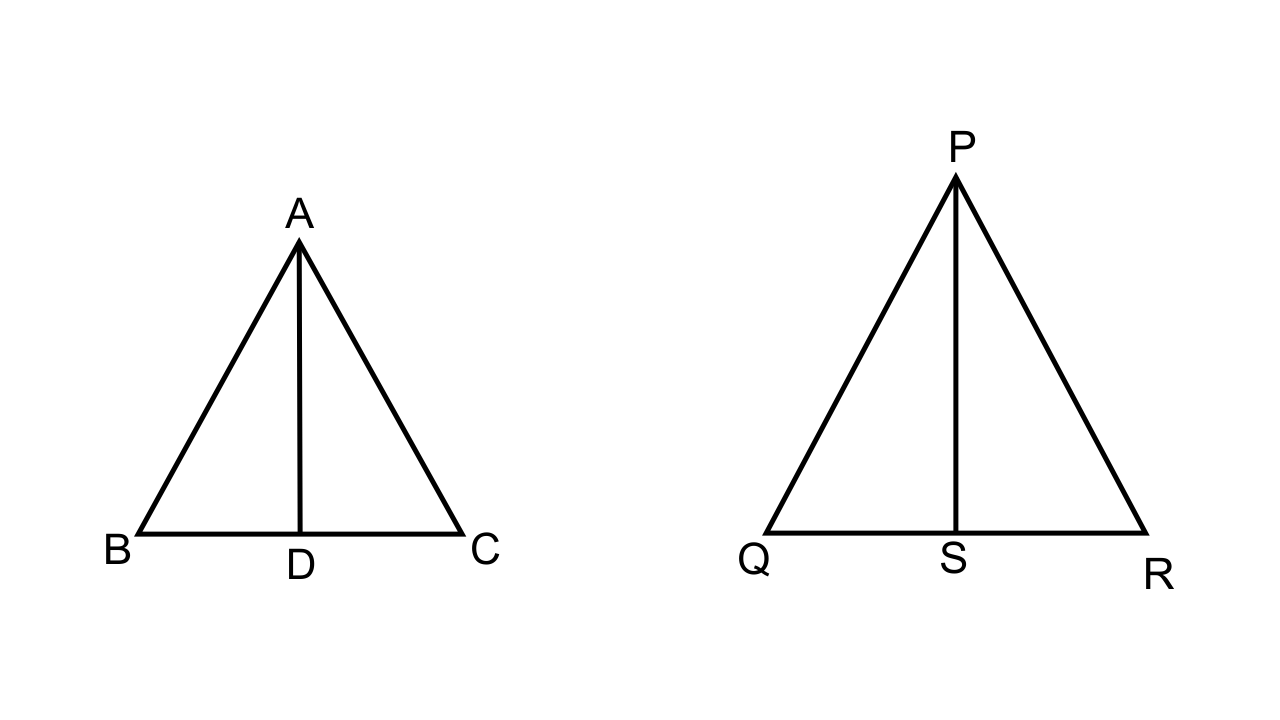
Let ABC and PQR be the two isosceles triangles which are mentioned. 

Then we have \[\dfrac{{AB}}{{AC}} = \dfrac{1}{1} = \dfrac{{PQ}}{{PR}}\]

Also, it is given that ∠A = ∠P 

Hence by SAS similarity, we can say that ∆ABC ~ ∆PQR

Let us consider that AD and PS are the altitudes of the respective triangles. 

It is known that the ratio of areas of the two similar triangles are equal to the square of their corresponding altitudes, hence we have 

\[\dfrac{{Area{\text{ of }}\Delta {\text{ABC}}}}{{Area{\text{ of }}\Delta {\text{PQR}}}} = {(\dfrac{{AD}}{{PS}})^2}\]

\[\dfrac{{AD}}{{PS}} = \dfrac{4}{5}.\]

23.In ∆ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA

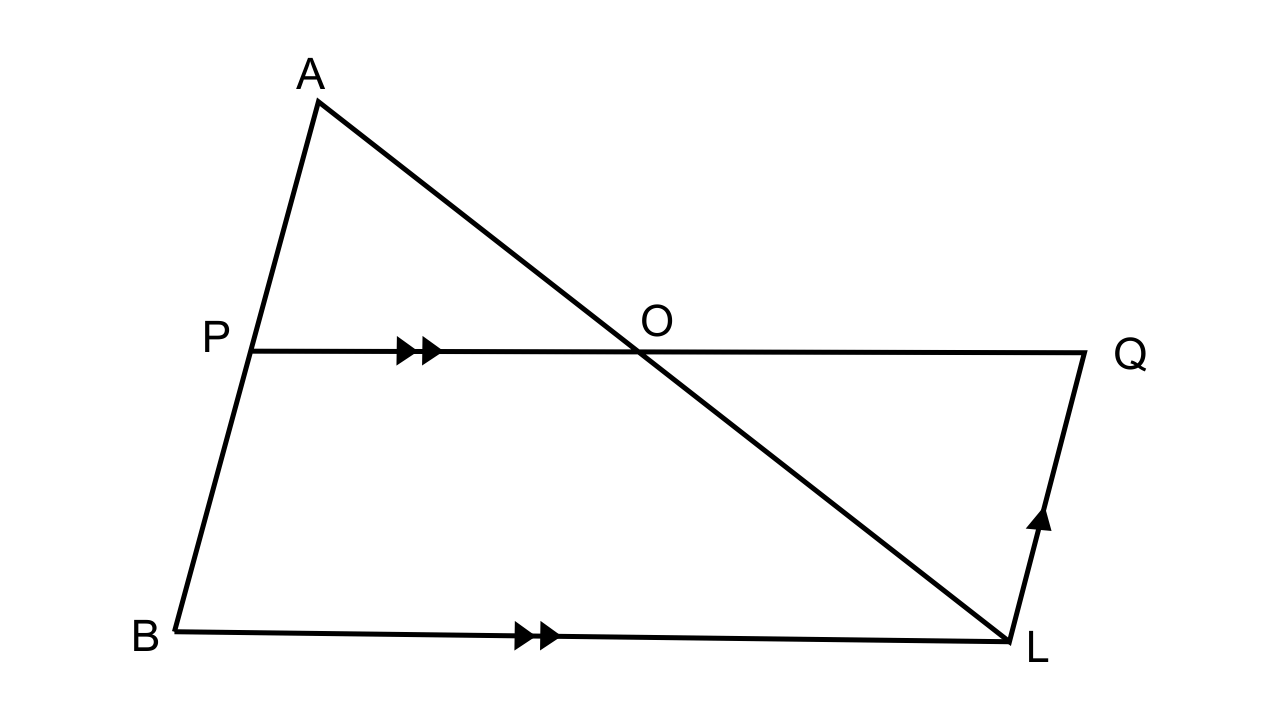
Find: (i) area ∆APO : area ∆ABC.

(ii) area ∆APO : area ∆CQO.

Ans: 

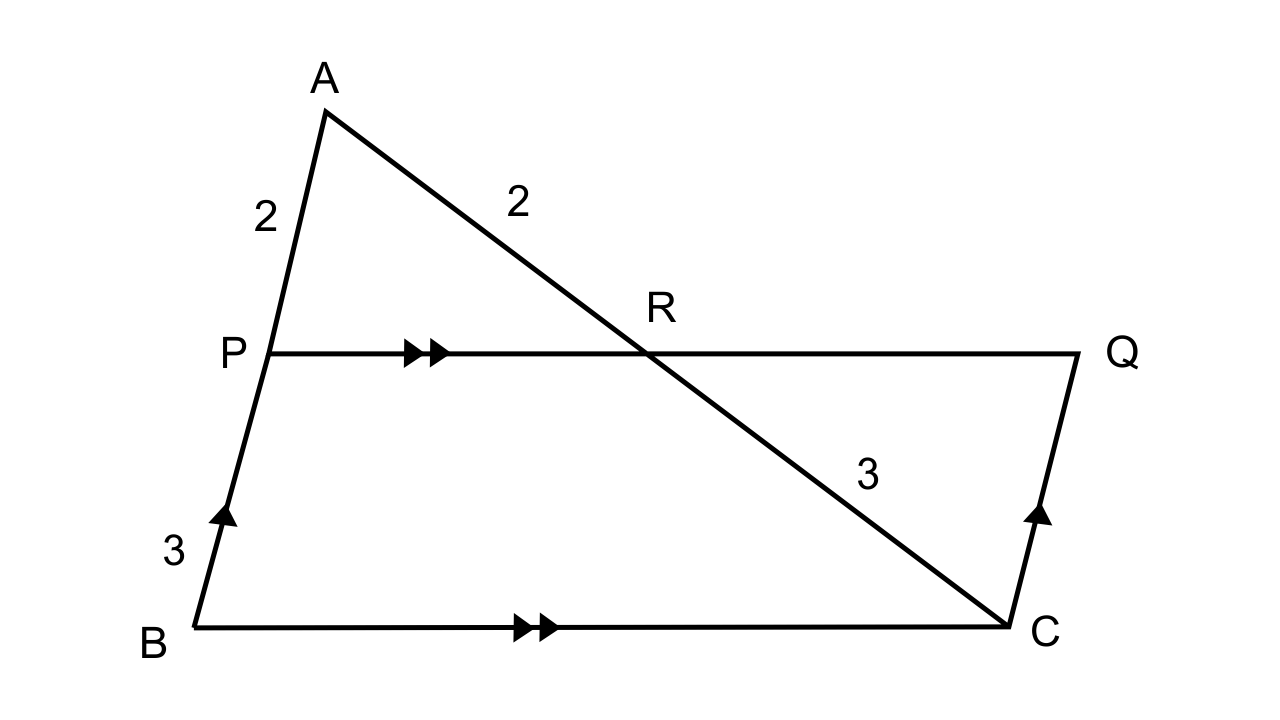
In ∆ABC,

AP : PB = 2 : 3

PQ || BC and CQ || BA

From the figure we can say that PQ || BC

∴\[\dfrac{{AP}}{{PB}} = \dfrac{{AO}}{{OC}} = \dfrac{2}{3}\]

(i) To find the area ∆APO : area ∆ABC. 

As we know that ∆APO ~ ∆ABC

∴\[\dfrac{{Area{\text{ }}\Delta {\text{APO}}}}{{Area{\text{ }}\Delta {\text{CQO}}}} = \dfrac{{A{P^2}}}{{A{B^2}}} = \dfrac{{A{P^2}}}{{{{(AP + PB)}^2}}} = \dfrac{4}{{25}}\]

Area ∆APO : Area ∆ABC= 4 : 25

(ii) Let us consider ∆APO and ∆CQO

∠APO = ∠OQC (Alternate angles)

∠AOP = ∠COQ (Vertically opposite angles)

Hence by AA axiom, we can say that ∆APO~ ∆CQO

∴\[\dfrac{{Area{\text{ }}\Delta {\text{APO}}}}{{Area{\text{ }}\Delta {\text{CQO}}}} = \dfrac{{A{P^2}}}{{P{B^2}}} = \dfrac{4}{9}\]

∴Area ∆APO :Area ∆CQO = 4:9 

24. The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.

Show that:

(i) ∆ADC ~ ∆BEG

(ii) CA × CE = CB × CD

(iii) ∆ABC ~ ∆DEC

(iv) CD × AB = CA × DE

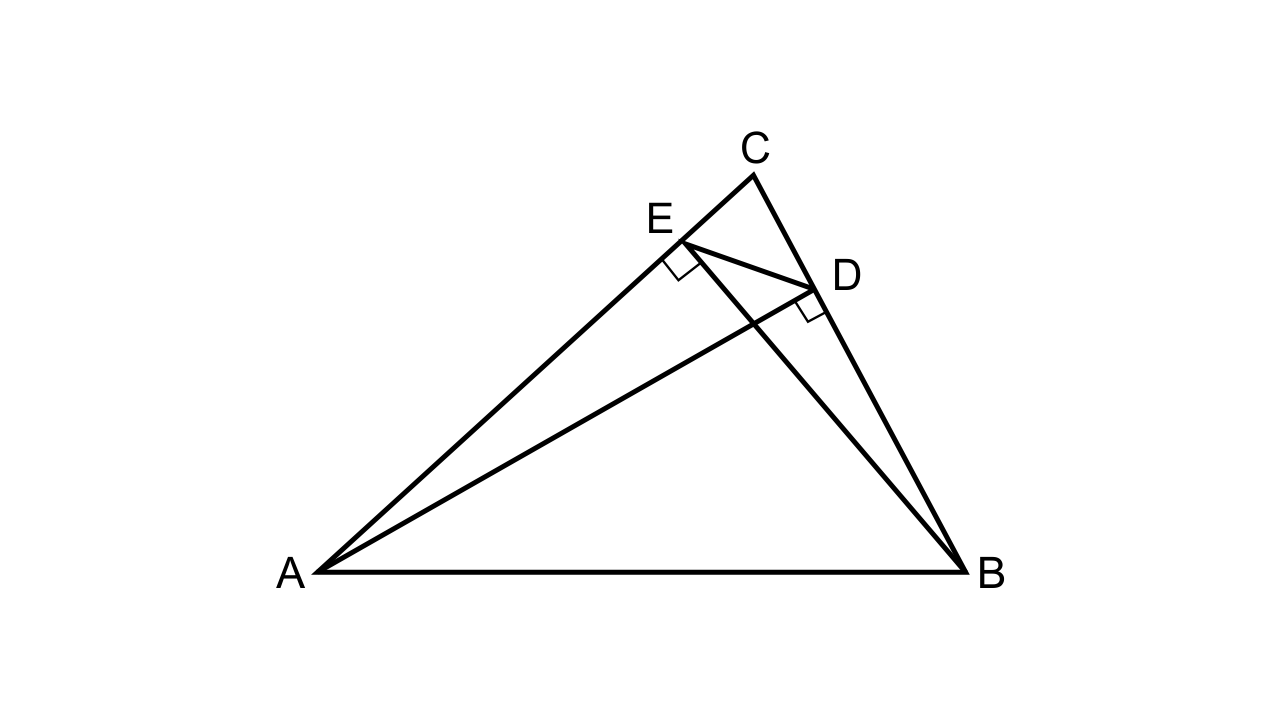
Ans:  It is given that 

In ∆ABC, AD ⊥ BC, and BE ⊥ AC, DE is joined

We have to prove:

(i) ∆ADC ~ ∆BEG

(ii) CA × CE = CB × CD

(iii) ∆ABC ~ ∆DEC

(iv) CD × AB = CA × DE

Proof:

(i) In ∆ADC and ∆BEC,

∠C = ∠C (common angle)

∠ABE = ∠BEC (as each angle is 90°)

Hence by AA axiom we can say that ∆ADC ~ ∆BEC 

(ii) As \[\dfrac{{CA}}{{CB}} = \dfrac{{CD}}{{CE}}\]

Hence, CA × CE = CB × CD

(iii) Let us consider ∆ABC and ∆DEC

∠C = ∠C (common angle)

\[\dfrac{{CA}}{{CB}} = \dfrac{{CD}}{{CE}}\](already proven)

Hence by SAS axiom, we can say that ∆ABC ~ ∆DEC

(iv)\[\dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CE}} = \dfrac{{AB}}{{DE}}\]

\[\dfrac{{CA}}{{CD}} = \dfrac{{AB}}{{DE}}\]

Now, CD × AB = CA × DE hence, proved. 

25. In the given figure, ABC is a triangle-with ∠EDB = ∠ACB. Prove that ∆ABC ~ ∆EBD.

If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ∆BED = 9 cm². Calculate the

(i) length of AB

(ii) area of ∆ABC

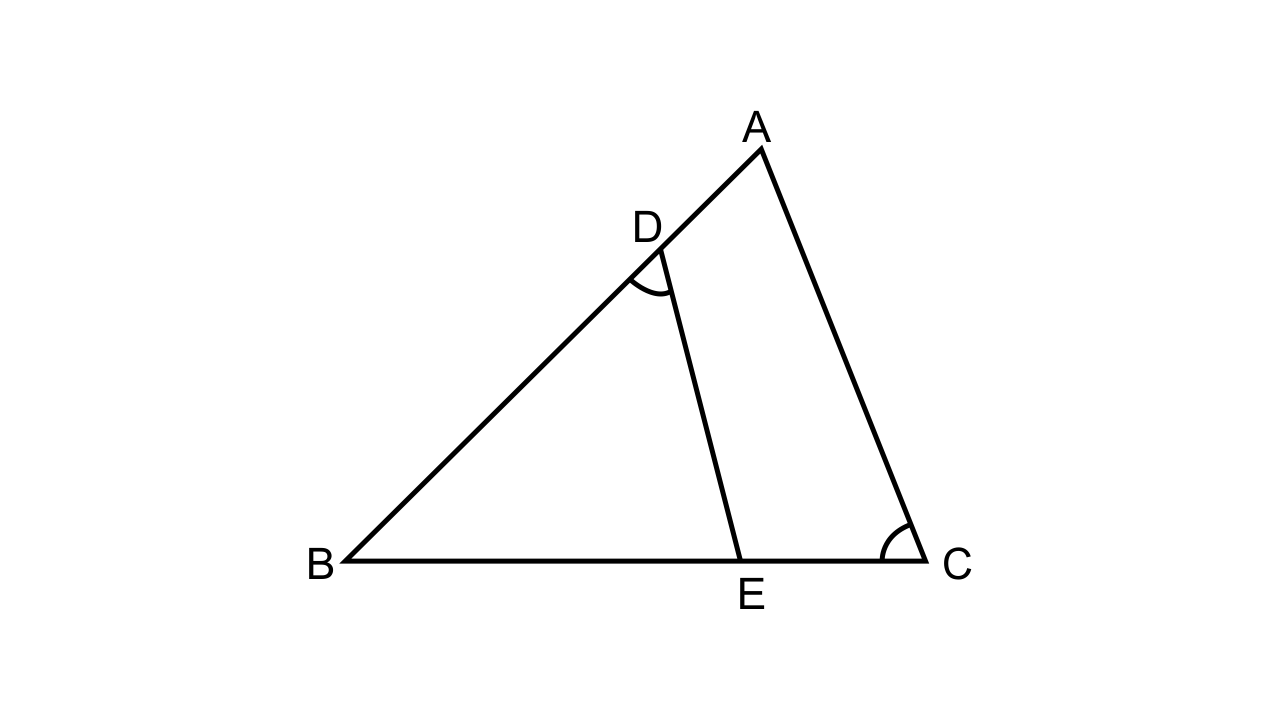
Ans:  

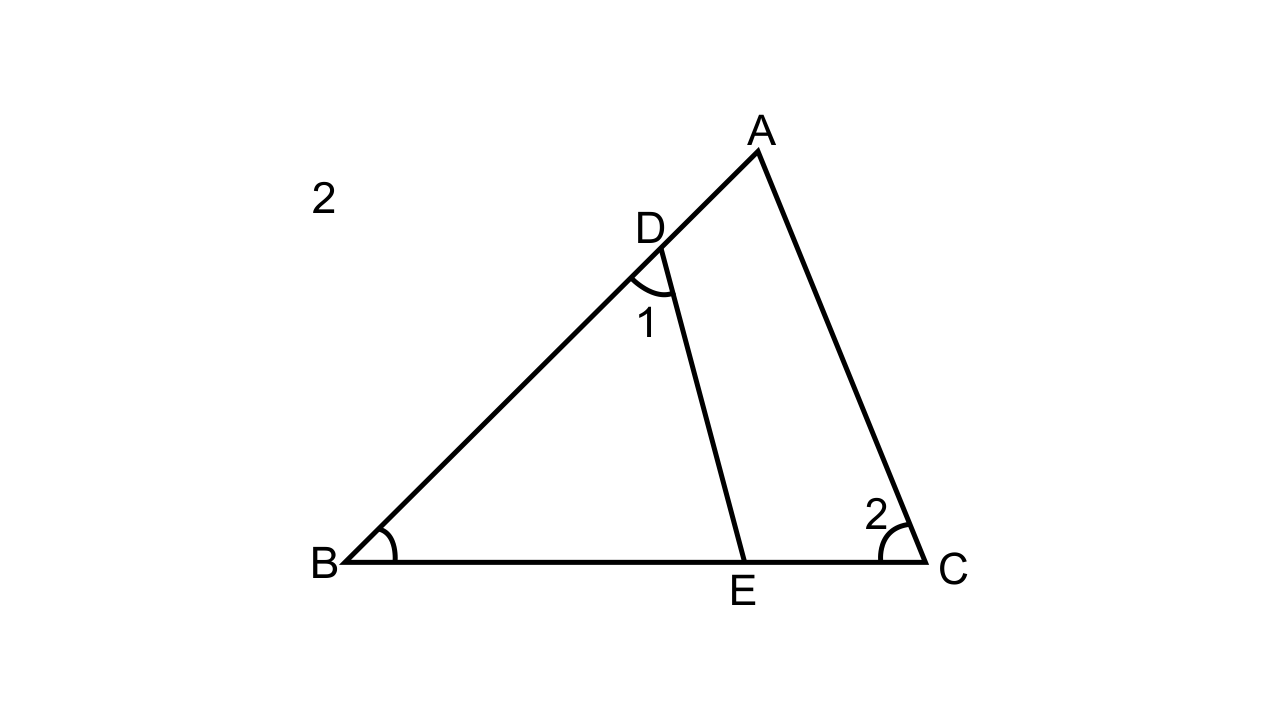
Let us consider ∆ABC and ∆EBD

∠1 = ∠2 (given in the diagram)

∠B = ∠B (common angles)

∆ABC ~ ∆EBD.

Now, \[\dfrac{{Area{\text{ of }}\Delta {\text{ABC}}}}{{Area{\text{ of }}\Delta {\text{EBD}}}} = {(\dfrac{{BC}}{{BD}})^2}\]

\[\dfrac{{Area{\text{ of }}\Delta {\text{ABC}}}}{9} = {(\dfrac{{10}}{5})^2}\]

Area of ∆ABC = 36 cm²

\[\dfrac{{Area{\text{ of }}\Delta {\text{ABC}}}}{{Area{\text{ of }}\Delta EBD}} = {(\dfrac{{AB}}{{BE}})^2}\]

\[\dfrac{{36}}{9} = \dfrac{{A{B^2}}}{{36}}\]

Now, AB = 12cm 

26. In the given figure, ABC is a right-angled triangle with ∠BAC = 90°.

(i) Prove ∆ADB ~ ∆CDA.

(ii) If BD = 18 cm, CD = 8 cm, find AD.

(iii) Find the ratio of the area of ∆ADB is to area of ∆CDA

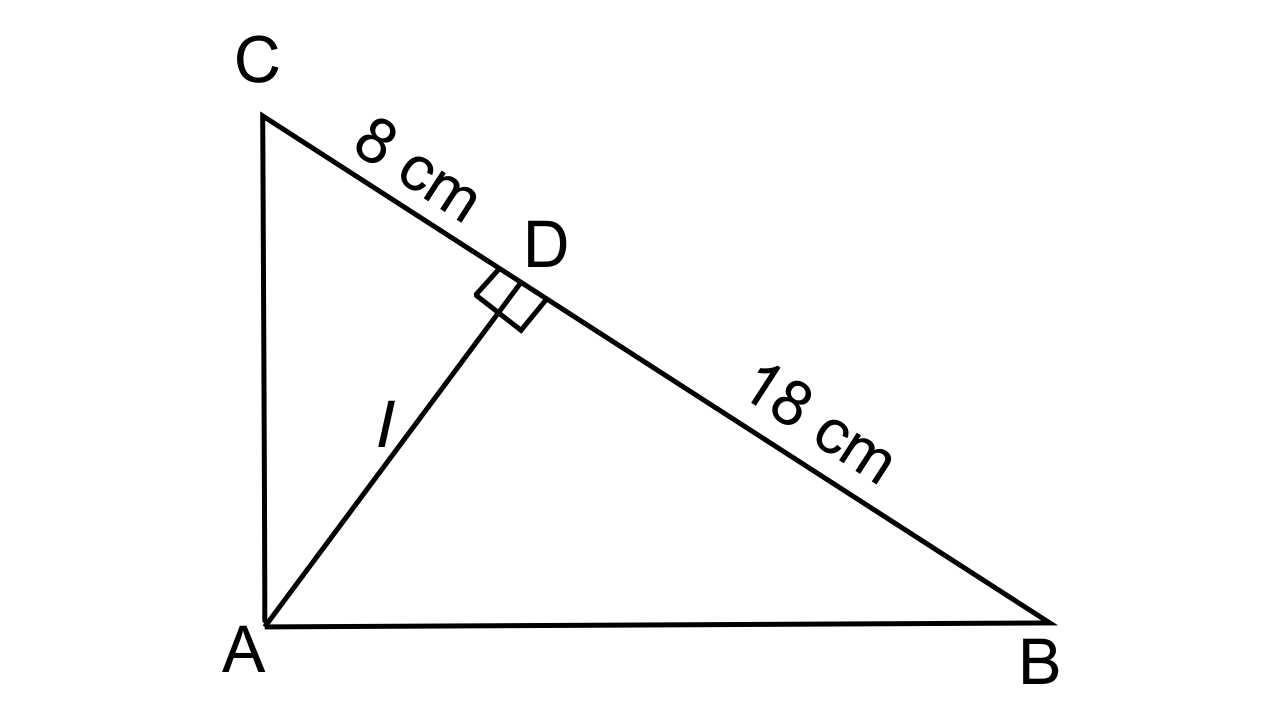
Ans: 

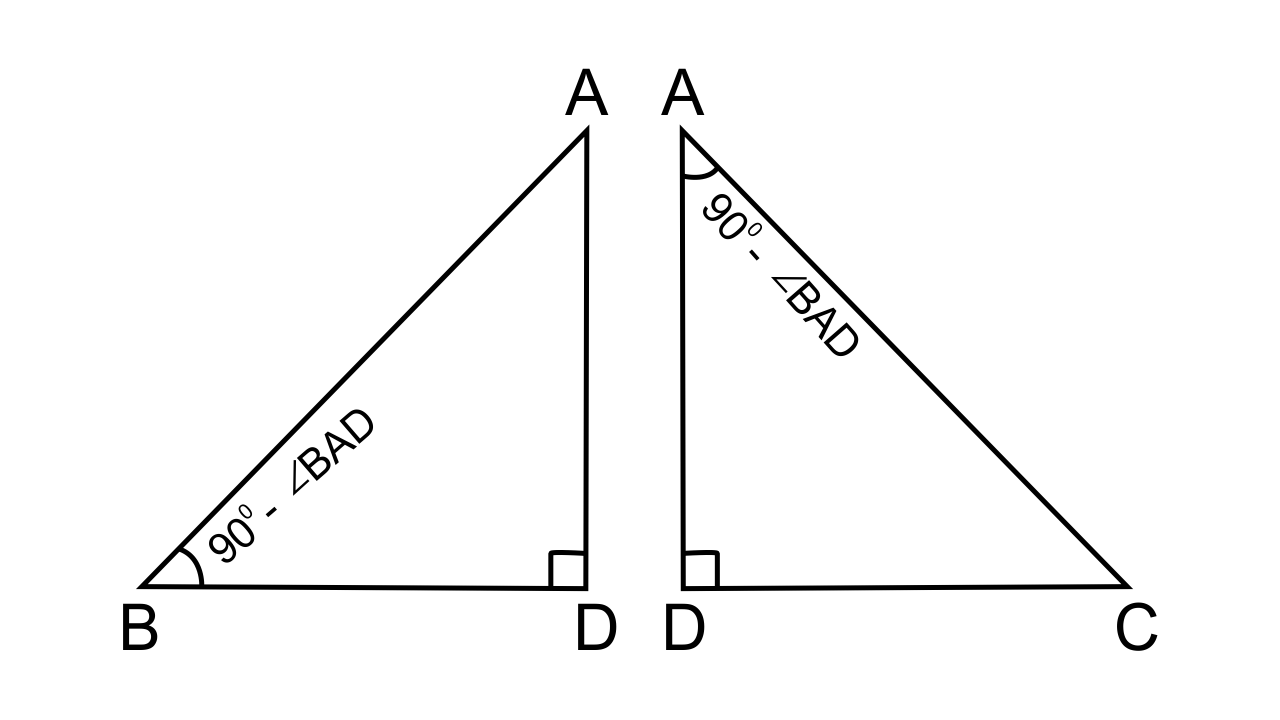
(i) Let us consider ∆ADB and ∆CDA :

∠ADB = ∠ADC [ As each angle = 90°]

∠ABD = ∠CAD [each = 90° – ∠BAD]

Hence by the AA similarity axiom, we can say that ∆ADB ~ ∆CDA 

(ii) Since, ∆ADB ~ ∆CDA

∴\[\dfrac{{AD}}{{CD}} = \dfrac{{BD}}{{AD}}\]

AD = \[\sqrt {144}  = 12cm\]

(iii)To find the ratio of the area of ∆ADB is to area of ∆CDA

\[\dfrac{{area{\text{ of }}\Delta {\text{ADB}}}}{{area{\text{ of }}\Delta {\text{CDA}}}} = \dfrac{{B{D^2}}}{{A{D^2}}} = 9.4\]

27. In the given figure, AB and DE are perpendicular to BC.

(i) Prove that ∆ABC ~ ∆DEC

(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.

(iii) Find the ratio of the area of ∆ABC : area of ∆DEC.

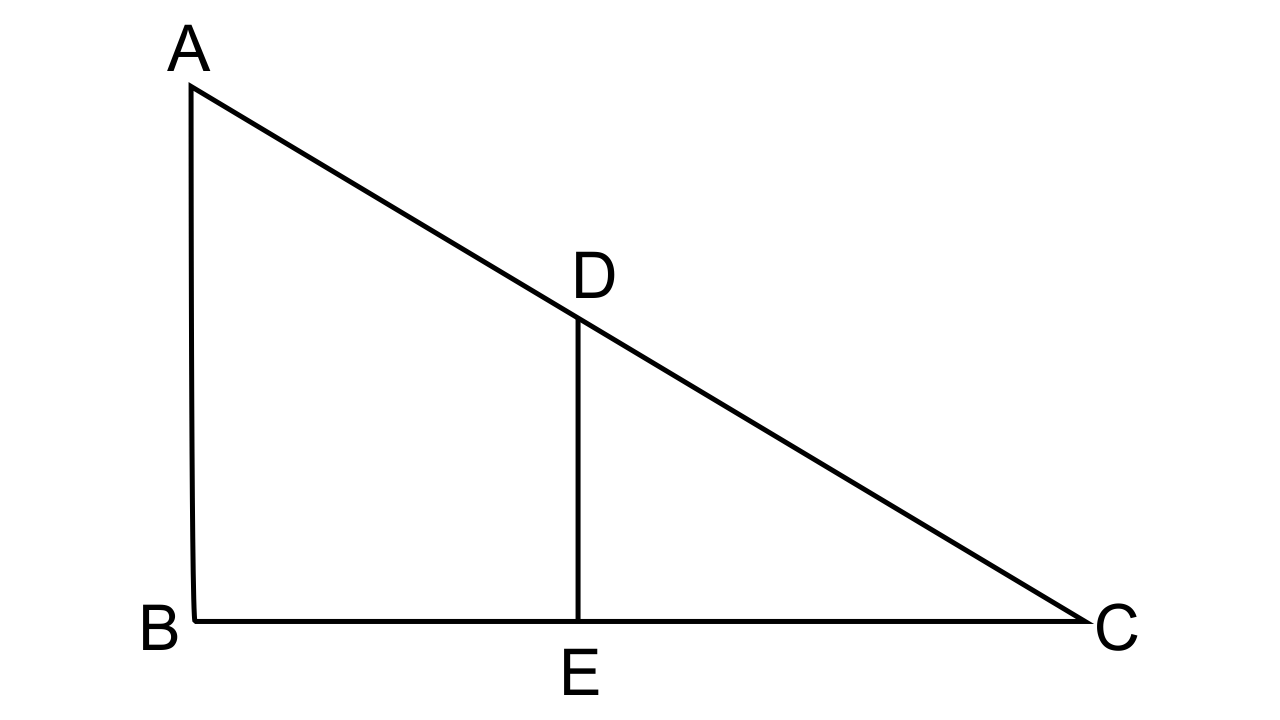
Ans:  

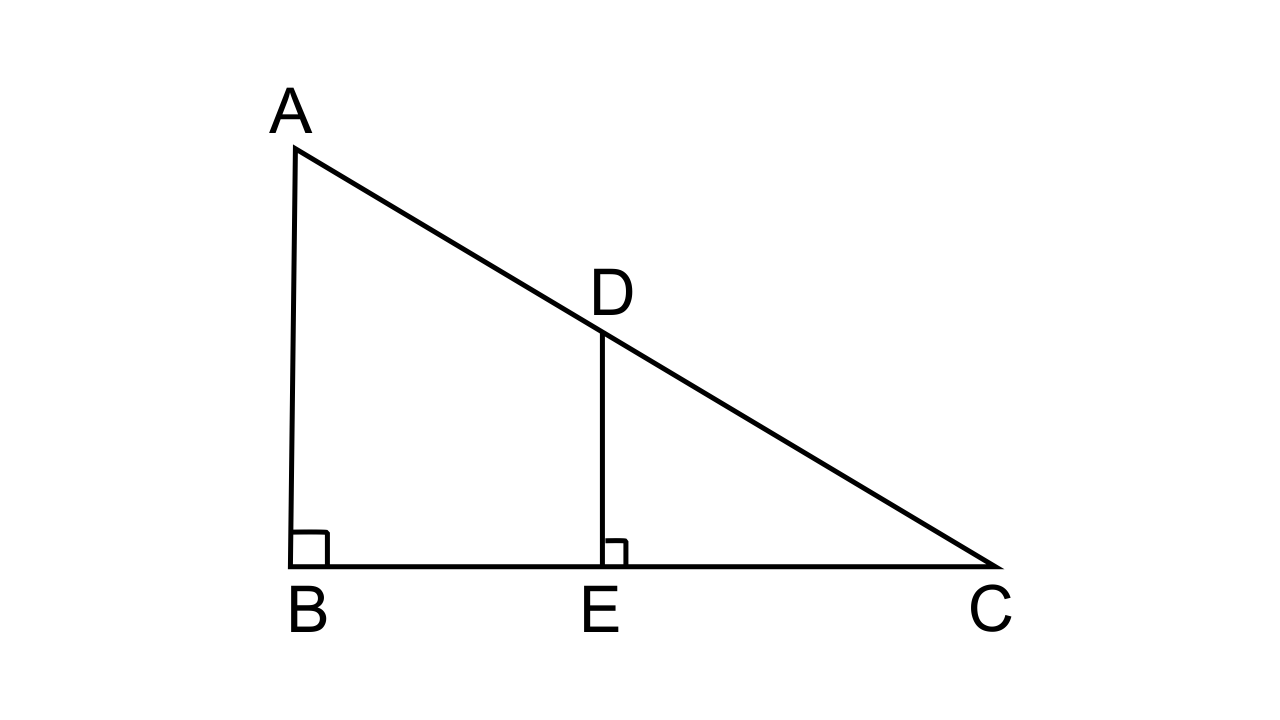
(i) To prove that ∆ABC ~ ∆DEC

Let us consider In ∆ABC and ∆DEC

∠ABC = ∠DEC (As each = 90°)

∠C = ∠C (common angles)

∆ABC ~ ∆DEC (by AA axiom)

(ii) \[\dfrac{{AC}}{{DC}} = \dfrac{{AB}}{{DE}}\]

\[\dfrac{{15}}{{CD}} = \dfrac{6}{4}\]

CD = 10 cm 

(iii) \[\dfrac{{area{\text{ of }}\Delta {\text{ABC}}}}{{area{\text{ of }}\Delta DEC}} = {(\dfrac{{AB}}{{DE}})^2} = \dfrac{{36}}{{16}} = 9.4\]

28.ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that:

(i) ∆ADE ~ ∆ACB.

(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.

(iii) Find, area of ∆ADE : area of quadrilateral BCED.

Ans:  From the given figure we can figure out that 

∆ABC is a right-angled triangle at a right angle at B.

D is any point on AB and DE ⊥ AC

Proof:

(i) Let us consider ∆ADE and ∆ACB

∠A = ∠A (common angles)

∠E = ∠B (each angle is = 90°)

By AA axiom we can say that ∆ADE ~ ∆ACB. 

(ii) It is given that AC = 13 cm, BC = 5 cm, AE = 4 cm

And we know that ∆ADE ~ ∆ACB.

\[\dfrac{{AD}}{{AC}} = \dfrac{{AE}}{{AB}} = \dfrac{{DE}}{{BC}}\](As corresponding sides are proportional)

\[\dfrac{{AD}}{{13}} = \dfrac{4}{{12}} = \dfrac{{DE}}{5}\]

AD = 4 \[\dfrac{1}{3}\]cm and 

DE = \[\dfrac{5}{3}\]cm 

(iii) To find the area of ∆ADE : area of quadrilateral BCED

Area of ∆ ABC = ½ × BC × AB= ½ × 5 × 12 = 30 cm²

Now area of ∆ADE = 

Area of quadrilateral BCED= Area of ∆ ABC - area of ∆ADE

= \[30 - \dfrac{{10}}{3} = \dfrac{{80}}{3}\]

Thus the area of ∆ADE : Area of quadrilateral BCED =\[\dfrac{{10}}{3}:\dfrac{{80}}{3}\]= 1: 8

29.Given: AB // DE and BC // EF. Prove that:

(i) \[\dfrac{{AD}}{{DG}} = \dfrac{{CF}}{{FG}}\]

(ii) ∆DFG ~ ∆ACG.

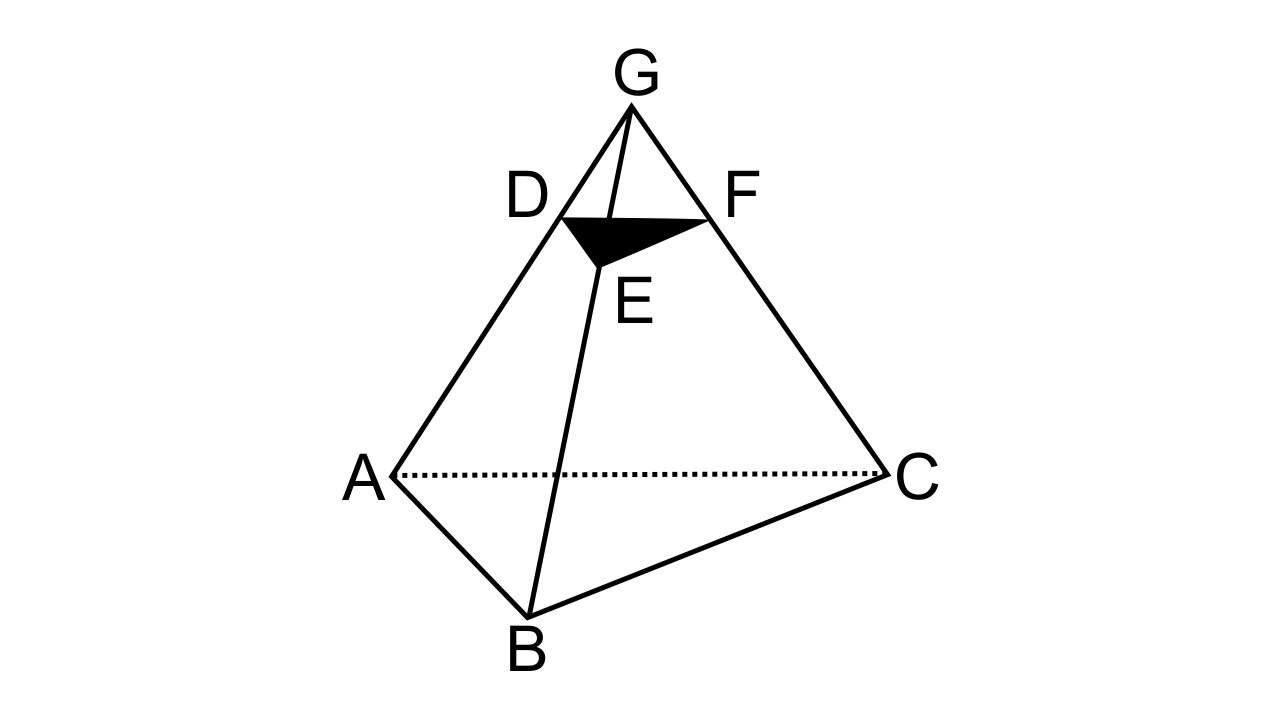
Ans:  (i) Let us consider ∆AGB, in which DE // AB.

Now by the basic proportionality theorem, we have, 

\[\dfrac{{GD}}{{DA}} = \dfrac{{GE}}{{EB}}\]………..(1)

In ∆GBC, in which EF // BC.

Now by the basic proportionality theorem, we have,

\[\dfrac{{GD}}{{DA}} = \dfrac{{GE}}{{FC}}\]

\[\dfrac{{AD}}{{DG}} = \dfrac{{CF}}{{FG}}\]

(ii) To show that ∆DFG ~ ∆ACG.

\[\dfrac{{AD}}{{DG}} = \dfrac{{CF}}{{FG}}\]

∠DGF = ∠AGC (Common angle)

Hence, by SAS similarity, we can say that ∆DFG ~ ∆ACG.

Introduction to the Chapter

This chapter teaches the students how two figures have the same shape but differ in size and yet they are called similar figures. This chapter mainly deals with the similarity of triangles, basics of understanding corresponding sides and corresponding angles of similar triangles, various conditions for similarity of two triangles, the Basic Proportionality theorem, the relation between the areas of two triangles, similarity as a size transformation, and finally the applications to maps and models are the main concepts of the chapter.

ICSE Class 10 Maths Solutions to Chapter 15

Students can refer to the ICSE solutions to clarify the doubts pertaining to the chapter which are curated by expert professionals having deep knowledge of the subject. All the solutions are created so that the students can learn easily and also, gain confidence.

Vedantu’s ICSE solution has all the questions solved with minute steps in detail. Students can easily learn and score well in the exam. Students should practice and solve on their own with logical thinking. This practice will help them to get familiarized with a variety of problems that can be solved during the exam.

Students should make notes of the key point in the chapter. The formulas and the theorems should be noted in the notes so that it becomes easy to remember.

The solutions of class 10 Maths are very important and have to be systematic and very organized. The solutions give a glance at the whole syllabus in a short duration.

The solutions are the best study material that helps the students to revise accurately and reduce their stress levels.

Maths is one of the core subjects and they are the stepping stone and play a very crucial role in everyone’s future. Class 10 ICSE Maths is very interesting with many new topics and concepts. Practicing every day and learning with understanding will help to get the appropriate grip on the subject.