NCERT Exemplar for Class 6 Maths Solutions Chapter 9 Symmetry & Practical Geometry

Solved Examples

In Examples 1 and 2 , Out of Four Given Options, Only One is Correct. Write the Correct Answer.

Example 1: Which of the following letters does not have any line of symmetry?

(A) $\mathrm{E}$

(B) $\mathrm{T}$

(C) $\mathrm{N}$

(D) $\mathrm{X}$

Ans: Correct answer is (c)

Example 2: Which of the following angles cannot be constructed using ruler and compasses?

(A) $75^{\circ}$

(B) $15^{\circ}$

(C) $135^{\circ}$

(D) $85^{\circ}$

Ans: Correct answer is (D)

In Examples 3 to 5 , Fill in the Blanks So That the Statements Are True:

Example 3: If B is the image of A in line $l$ and D is the image of C in line $l$, then AC =_____

Ans: BD

Example 4: In Fig. 9.1, the line segments PQ and RQ have been marked on a line $l$ such that $\mathrm{PQ}=\mathrm{AB}$ and $\mathrm{RQ}=\mathrm{CD}$.

Then AB - CD =_____.

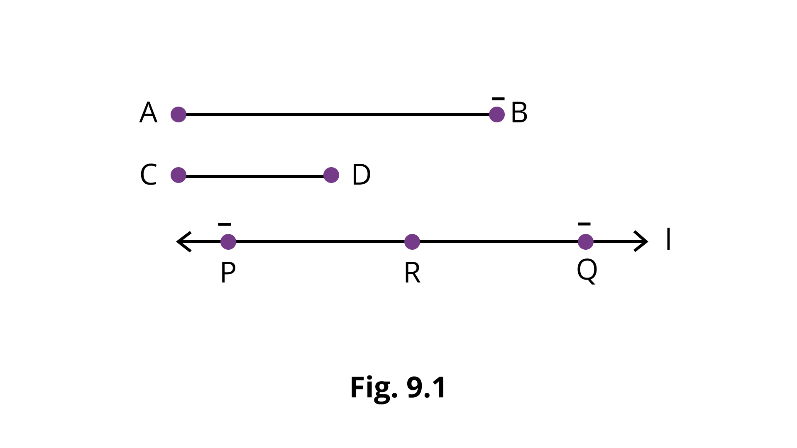
Ans: PR

Example 5: The number of scales in a protractor for measuring the angles is

Ans: Two

In Examples 6 and 7, State Whether the Statements Are True or False:

Example 6: Using the set squares  $30^{\circ}-60^{\circ}-90^{\circ} \text { and } 45^{\circ}-45^{\circ}-90^{\circ}$ we can draw an angle of  $75^{\circ}$. 

Ans: True. (Since  $75^{\circ}=45^{\circ}+30^{\circ}$ )

Example 7: A circle has only 8 lines of symmetry. 

Ans: False (A circle has infinitely many lines of symmetry).

Example 8. Write the letters of the word ALGEBRA which have no line of symmetry. Ans: The letters L, G and R have no line of symmetry. (Do you see why the dotted line is not the line of symmetry in

Example 9: Draw a line segment equal to the sum of two line segments given in Fig. 9.2

Ans: 1. Draw a line l and on it, cut a line segment PQ = AB, using compasses. ( Fig. 9.3 ) 

2. With Q as centre and CD as radius, draw an arc to cut a line segment QS = CD on l as shown in Fig. 9.4. Then, line segment PS is equal to the sum of AB and CD, i.e., PS = AB + CD

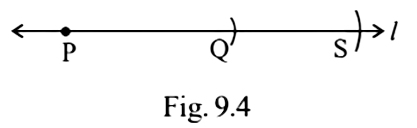
Example 10. Draw an angle equal to the difference of two angles given in Fig. 9.5.

Ans: 1. Draw an angle ABC equal to ∠DEF (as ∠DEF > ∠PQR), using ruler and compasses. 

2. With BC as one of the arms, draw an angle SBC equal to ∠PQR such that BS is in the interior of ∠ABC as shown in Fig. 9.6. Then, ∠ABS is the required angle which is equal to ∠DEF – ∠PQR. (Note: For making ∠ABS = ∠DEF – ∠PQR, how will you draw ray BS?)

Example 11. Complete Fig. 9.7 so that l is the line of symmetry of the completed figure. l Fig. 9.7 

Ans: The figure can be completed as shown in Fig. 9.8, by drawing the points symmetric to different corners(points) with respect to line l.

Exercise :

In Questions 1 to 17, Out of the Given Four Options, Only One is Correct. Write the Correct Answers.

1. In the following figures, the figure that is not symmetric with respect to any line is:

(A) (i) 

(B) (ii) 

(C) (iii) 

(D) (iv)

Ans: Option B is correct

             i.

It has two lines of symmetry so, option (a) is not correct.

           ii.

It has no line of symmetry; it means it is non symmetric with respect to any line, so option (b) is correct.

iii.

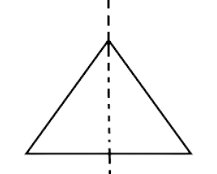
it has one line of symmetry and if it is an equilateral triangle then this has three lines of symmetry so, option (C) is incorrect.

        iv.

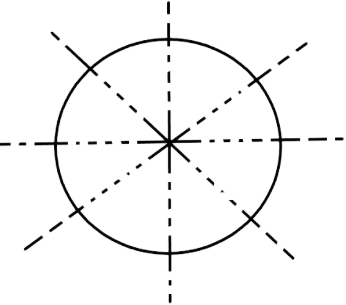
It has an infinite line of symmetry so, option (D) is incorrect.

2. The number of lines of symmetry in a scalene triangle is

 (A) 0   

(B) 1  

(C) 2 

(D) 3 

Ans: Option A is correct

A scalene triangle has zero line of symmetry. So option (A) is correct.

3. The number of lines of symmetry in a circle is 

(A) 0  

(B) 2  

(C) 4  

(D) more than 4

Ans: Option D is correct

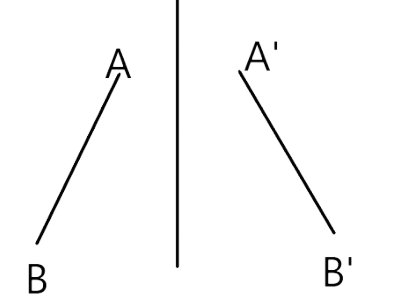
A circle has infinity or more than 4 lines of symmetry. So option (D) is correct.

4. Which of the following letters does not have the vertical line of symmetry?

 (A) M     

(B) H    

(C) E    

(D) V

Ans: Option D is correct

In the circle, a line (drawn at any angle ) that goes through Its centre is a line of symmetry. So a circle has infinite lines of symmetry.

Correct option [D].

5. Which of the following letters have both horizontal and vertical lines of symmetry?

(A) X     

(B) E    

(C) M     

(D) K

Ans: Option A is correct

X has both horizontal and vertical lines of symmetry. Because we draw two lines. One is vertical and the second is Horizontal.Correct option is  (A).

6. Which of the following letters does not have any line of symmetry?

(A) M     

(B) S    

(C) K    

(D) H

Ans:Option B is correct

(A). M, It has one line of symmetry so option (A) is incorrect.

(B). S, It has no line of symmetry so option (B) is correct.

(C). K,it has only one line of symmetry so option (C) is incorrect.

(D). H,It has two lines of symmetry so option (D) is incorrect.

7. Which of the following letters has only one line of symmetry?

(A) H   

(B) X    

(C) Z       

(D) T

Ans:Option D is correct

1. H,It has two lines of symmetry so option (A) is incorrect.

2. X,It has two line of symmetry so option (B) is incorrect.

3. Z,It has no line of symmetry so option (C) is incorrect.

4. T,It has two lines of symmetry so option (D) is correct.

8. The instrument to measure an angle is a

(A) Ruler 

(B) Protractor 

(C) Divider 

(D) Compasses

Ans: Option B is correct

(A) Ruler:A ruler is an instrument when is either used to find the length of a line drawn or to draw a straight line fixed length so it cannot be used to measure angles.So option (A) is incorrect.

(B)  protractor:A protractor is an instrument when is generally divided into 180 equals parts and it is used for making and measuring angle.

So option (B) is correct.

(C)  Divider: A divider is an instrument for measuring transferring or making off distance. It cannot be used to measure angles.

So option (C) is incorrect.

(D)  compass: A compass is a technical drawing instrument that can be used for inscribing circles or are.

They cannot be used for measuring angles.

So option (D) is incorrect.

9. The instrument to draw a circle is

(A) Ruler 

(B) Protractor 

(C) Divider 

(D) Compasses
Ans:Option D is correct

(A) Ruler: Ruler is an instrument which is either used to find the length of a line drawn or to draw a straight line fixed length so it cannot be used for drawing circle.

So option (A) is incorrect.

(B)Protractor:A protractor is an instrument which is generally divided into 180 equal parts and it can not be used for drawing circles.

So option (B) is incorrect.

(C) Divider: A divider is an instrument for measuring transferring or making off distance. It cannot be used for drawing circles.

So option (C) is incorrect.

(D)Compass: A compass is a technical drawing instrument that can be used for Drawing circles or arc.

It can be used for drawing a circle.

So option (D) is correct.

10. The number of set squares in the geometry box is

(A) 0   

(B) 1   

(C) 2   

(D) 3

Ans: option (C) is correct

We have 2 set squares in the geometry box.

So option (C) is correct.

11. The number of lines of symmetry in a ruler is

(A) 0   (B) 1   (C) 2   (D) 4

Ans: Option (C) is correct.

The line of symmetry can divide an object in that two halves each other.Ruler is a symmetric object. The ruler is in rectangular shape and there are two lines of symmetry.

Option (C) is correct.

12. The number of lines of symmetry in a divider is

(A) 0   

(B) 1    

(C) 2   

(D) 3

Ans: Option (B) is correct

The lines of symmetry are those lines that divide an object in two same parts; the divider has only one line of symmetry.

13. The number of lines of symmetry in compasses is

(A) 0    

(B) 1     

(C) 2     

(D) 3

Solution:Option (A) is correct

 Symmetrical lines divide an object into two parts. Both parts are same in size             compasses have no line of symmetry.

14. The number of lines of symmetry in a protractor is

(A) 0     

(B) 1     

(C) 2     

(D) more than 2

Ans: Option (B) is correct

The line of symmetry divides an object into two same size and shape parts.

The protractor is a symmetrical object so it has a line of symmetry.

15. The number of lines of symmetry in a $45^{\circ}-45^{\circ}-90^{\circ}$ set-square is

(A) 0     

(B) 1     

(C) 2     

(D) 3

Ans: Option (B) is correct

There are two types of set-square

$45^{\circ}-45^{\circ}-90^{\circ}$

$30^{\circ}-60^{\circ}-90^{\circ}$

Set-square has only one line of symmetry. Because it has the shape of a right angle triangle.

16. The number of lines of symmetry in a $30^{\circ}-60^{\circ}-90^{\circ}$ set square is

(A) 0

(B) 1

(C) 2

(D) 3

Ans: Option (A) is correct 

In the set-square of $30^{\circ}-60^{\circ}-90^{\circ}$ have no line of symmetry.if the number of lines of symmetry in a $30^{\circ}-60^{\circ}-90^{\circ}$ set-square is zero, because it has the shape of a scalene right-angled triangle.

17. The instrument in the geometry box having the shape

of a triangle is called a

(A) Protractor 

(B) Compasses 

(C) Divider 

(D) Set-square

Ans: Option (D) is correct

The instrument in the geometry box has types of set-square.

Option (A) is wrong The protector has one line of symmetry.

Option (B) is wrong The compasses have no line of symmetry.

Option (C) is wrong The divider has one line of symmetry.

Option (D) is Correct.as The instrument in the geometry box having the shape of a triangle is called a set-square.

In Questions 18 to 42, Fill in the Blanks to Make the Statements True.

18. The distance of the image of a point (or an object) from the line of symmetry (mirror) is ________ as that of the point (object) from the line (mirror).

Ans: The distance of the image of a point ( or an object) from the line of symmetry (mirror)is same as that of the point (object) from the line (mirror).

An object and its image are always at the same distance from the surface of the mirror which is called the mirror line. Therefore the distance of the object from the mirror line is the same as the distance of the image from the mirror line.

19. The number of lines of symmetry in a picture of Taj Mahal is _______.

Ans: The number of lines of symmetry in a picture of taj-mahal is one.

An object in a picture by only in front-view can divide in only one line of symmetry.

20. The number of lines of symmetry in a rectangle and a rhombus are ______ (equal/unequal).

Ans: The line of symmetry divides an object in two halves and in the same distance, shape and size.

The number lines of symmetry in a rectangle and a rhombus are equal.

There are two lines of symmetry in a rectangle and a rhombus.

Two lines of Symmetry in rectangle      

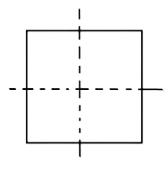
Two lines of Symmetry in rhombus  

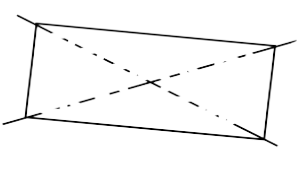
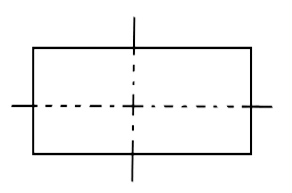
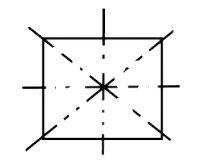
21. The number of lines of symmetry in a rectangle and a square are______ (Equal/unequal).

Ans: The number of lines of symmetry in a rectangle and a square are unequal.

Rectangle and square both are symmetrical objects and they have two and four lines of symmetry respectively.

Rectangle has two lines of symmetry

The square has four lines of symmetry.

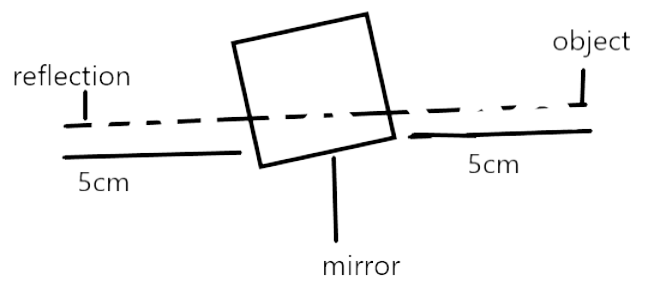
22. If a line segment of length $5 \mathrm{~cm}$ is reflected in a line of symmetry (mirror), then its reflection (image) is a ______  of measure ______ 

Ans: If a line segment of length $5 \mathrm{~cm}$ is reflected in a line of symmetry (mirror), then its reflection (image) is a Line Segment of the length $5 \mathrm{~cm}$.

A simple mirror shows the same reflection of an object at the same distance.

23. If an angle of measure 80o is reflected in a line of symmetry, then the reflection is a ______ of measure _______.

Ans: If an angle of measure 80° is reflected in a line of symmetry then the reflection is an angle of measure 80°.

Line of symmetry is that line which divides an object in two same size, same length and same angle parts.

24. The image of a point lying on a line l with respect to the line of symmetry l lies on _______.

Ans: The image of a point lying  on a line l with respect to the line of symmetry l lies on Iine l.

The reflection of a point will be on the same line if it is the line of symmetry.

25. In Fig. 9.10, if B is the image of the point A with respect to the line l and P is any point lying on l, then the lengths of line segments PA and PB are _______.

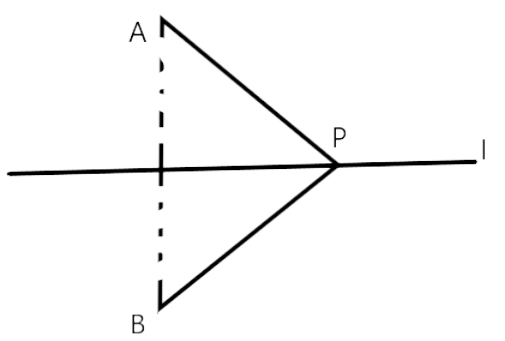
Ans: In figure 9.10, If B is the image of the point A with respect to the line I and P is any point lying on I, then the length at line segments PA and PB are equal.

The length of the line segment is always equal to their reflection because of the line of symmetry.

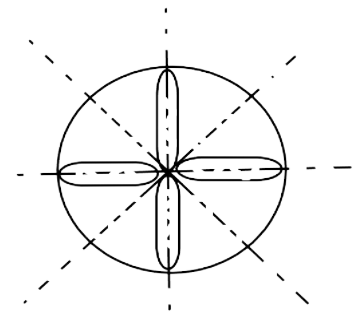
26. The number of lines of symmetry in Fig. 9.11 is__________.

Ans:  The number of lines of symmetry in figure 9.20 is 5 as it has 5 line of symmetry. 

27. The common properties in the two set-squares of a geometry box are that they have a __________ angle and they are of the shape of a __________.

Ans: The common properties in the two set-square of a geometry box are that they have a Right angle and they are of the shape of a Triangle.

There are two types of set-square in the geometry box.

$45^{\circ}-45^{\circ}-90^{\circ}$

$30^{\circ}-60^{\circ}-90^{\circ}$

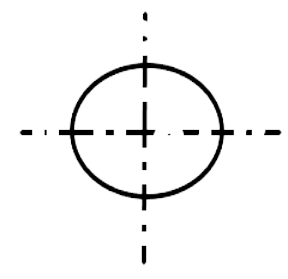
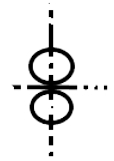
28. The digits having only two lines of symmetry are and The digits having only two lines of symmetry are $\underline{0}$ and $\underline{8}$.

Ans:  There are a total 10 digit $(0-9)$ present on number line but only $0 \& 8$ have two line of symmetry.

29. The digit having only one line of symmetry is __________.

Ans: The digit having only one line of symmetry is 3

               🡨 -------3------🡪

On the number line there are 0 to 9 numbers available but only 3 has one line of symmetry.

30. The number of digits having no line of symmetry is_________.

Ans:  The numbers of digits having no line of symmetry is 7

The numbers that have no line of symmetry like 1,2,4,5,6,7,and 9.

31. The number of capital letters of the English alphabets having an only vertical line of symmetry is________. 

Ans: The number of capital letters of the English alphabet having only a vertical line of symmetry is  7.  “A, M, T, U, V, Y and W” are capital letters of the English alphabet having only vertical lines of symmetry. Hence the answer is 7 alphabets.

32. The number of capital letters of the English alphabet having only horizontal lines of symmetry is________.

Ans:  The number of capital letters of the English alphabet having only horizontal lines of symmetry is 5.

“B, C, D, E and K” are capital letters of the English alphabet having only horizontal lines of symmetry. Hence the answer is 5 alphabets.

33. The number of capital letters of the English alphabets having both horizontal and vertical lines of symmetry is________.

Ans: The number of capital letters of the English alphabet having both horizontal and vertical lines of symmetry is 4.

“H, I, O, X are capital letters of the English alphabet having both horizontal and vertical lines of symmetry. Hence the answer is 4 alphabets. 

34. The number of capital letters of the English alphabets having no line of symmetry is__________.

Ans:  The number of capital letters of the English alphabet having no line of symmetry is 10.

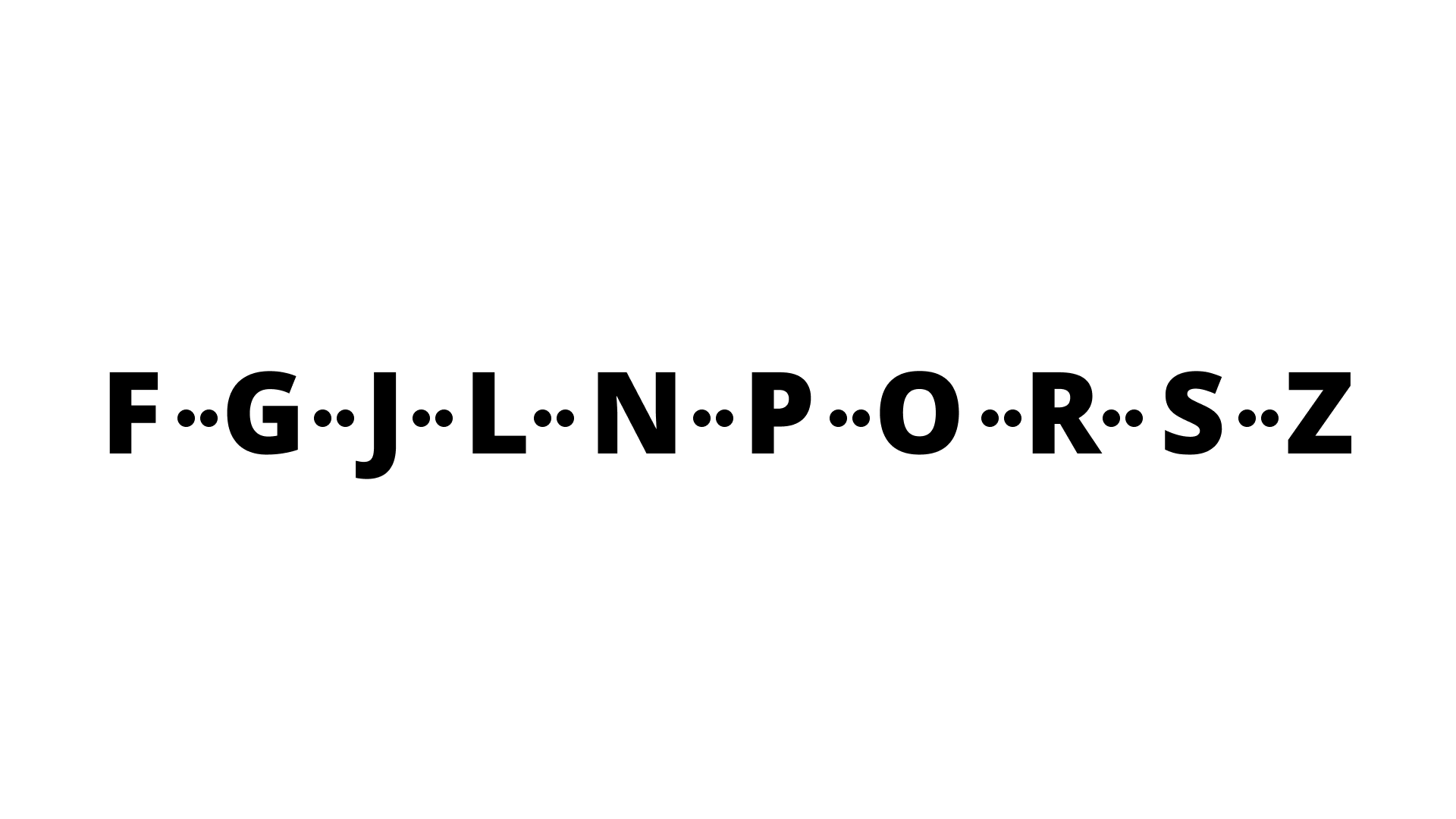
F, G, J, L, N, P, O, R, S and Z have no line of symmetry in the English alphabet. Hence the answer is 10 alphabets. 

35. The line of symmetry of a line segment is the ________ bisector of the line segment.

Ans: The line of symmetry of a line segment is the _ perpendicular bisector of the line segment.

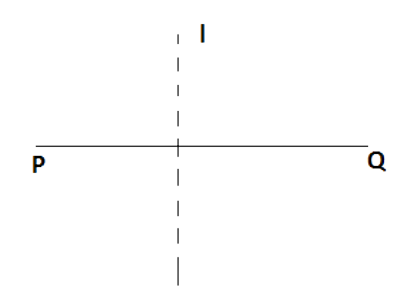
It is the perpendicular bisector that divides the line PQ into an equal line segment  I of symmetry. 

36. The number of lines of symmetry in a regular hexagon is __________.

Ans: The number of lines of symmetry in a regular hexagon is 6 .

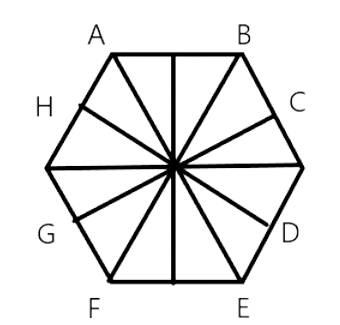
There are 6 lines of symmetry in a regular hexagon.

37. The number of lines of symmetry in a regular polygon of n sides’ is_______.

Ans: The number of lines of symmetry in a regular polygon of n sides’ is  n.

Suppose there is an ‘n’   number of lines of symmetry in a regular polygon of n sides. For example, a regular pentagon has 5 line symmetry, Hexagon has 6 line symmetry,  an octagon has 8 line symmetry, etc. 

38. A protractor has __________ line/lines of symmetry.

Ans: A protractor has ___one_______ line/lines of symmetry.

39. A 30° - 60° - 90° set-square has ________ line/lines of symmetry.

Ans: A 30° - 60° - 90° set-square has no line/lines of symmetry.

These set-squares have no line/lines of symmetry on the protractor because of the scalene right-angled triangle.

40. A $45^{\circ}-45^{\circ}-90^{\circ}$ set-square has line/lines of symmetry. 

Ans:  A $45^{\circ}-45^{\circ}-90^{\circ}$ set-square has one _line/lines of symmetry.

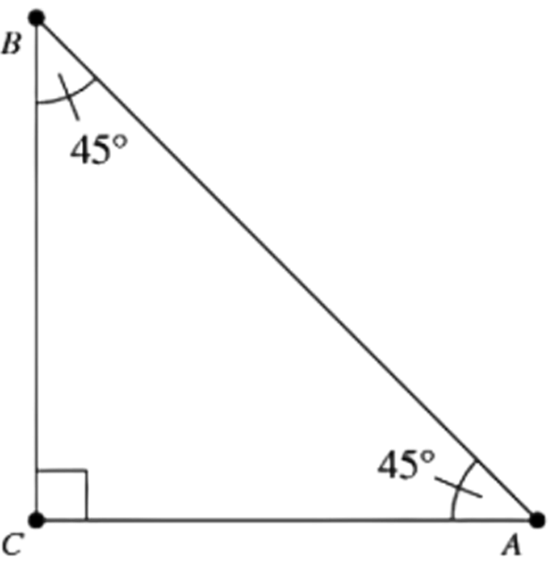
These set-squares have one line/lines of symmetry on the protractor because of the isosceles right-angled triangle.

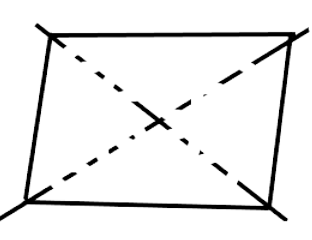
41.  A rhombus is symmetrical about diagonal.

Ans: A rhombus is symmetrical about each of its diagonal.

The lines of symmetry in a rhombus are from a vertex to the opposite vertex. So there will be two lines of symmetry.

42.  A rectangle is symmetrical about the lines joining the _____of the opposite sides.

Ans: A rectangle is symmetrical about the lines joining the point of the opposite sides

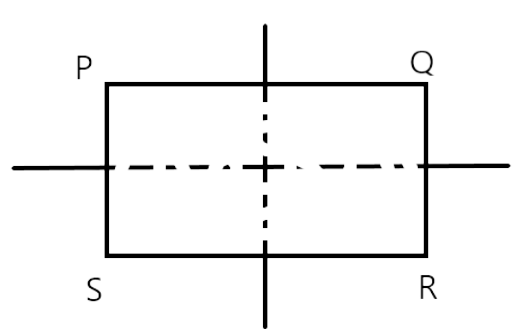
A rectangle is symmetrical about the lines joining the point of the opposite sides.

43. A right triangle can have at most one line of symmetry.

Ans: True

An isosceles right-angled triangle has only one line of symmetry.

But, a scalene right-angled triangle has no line of symmetry.

So, we can say that a right triangle can have at most one line of symmetry.

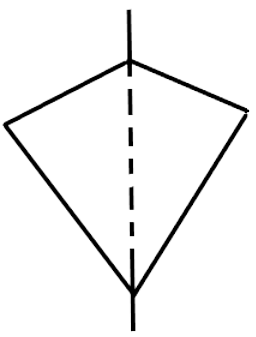
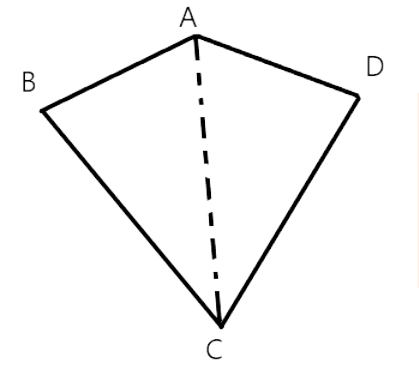
44. A kite has two lines of symmetry.

Ans: False

 The line of symmetry is a line segment that is drawn in between a diagram in order to make the diagram equally divided in two. The line of symmetry divides a picture into two parts so that one forms a mirror image of the other.

A kite has only 1line of symmetry as shown below.

45. A parallelogram has no line of symmetry.

Ans: True

 A parallelogram has no lines of symmetry . Some quadrilaterals such as rhombus, rectangle , square have lines of symmetry.

46. If an isosceles triangle has more than one line of symmetry, then it need not be an equilateral triangle.

Ans: True

 If an isosceles triangle has more than one line of symmetry, then it must be an equilateral triangle. Only equilateral triangles have 3 (more than 1) lines of symmetry.

47. If a rectangle has more than two lines of symmetry, then it must be a square.

Ans: True

The given statement is true as A rectangle with more than two lines of symmetry ,is a Square.

48. With ruler and compasses, we can bisect any given line segment.

Ans: True

A perpendicular bisector is a line segment which is perpendicular to the given line and divides the given line segment into two equal halves.With ruler and compass, we can draw a perpendicular bisector for any line segment.

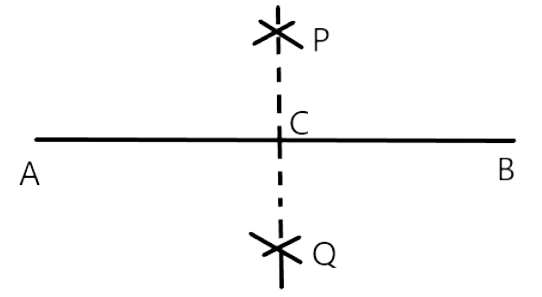
49. Only one perpendicular bisector can be drawn to a given line segment.

Ans: True

For a line segment there can only be one perpendicular bisector because at each point on a line segment only one perpendicular can be drawn and a perpendicular bisector passes through a single fixed point which is the midpoint.

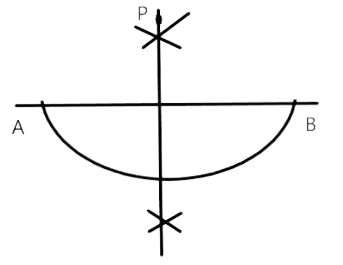
50. Two perpendiculars can be drawn to a given line from a point not lying on it.

Ans: True

Through a given line and a point (not lying on the line), only one perpendicular can be drawn as shown in the figure below.

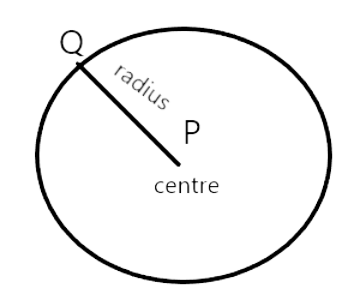
51. With a given centre and a given radius, only one circle can be drawn.

Ans: True .

This statement is true, because with the given centre and a given radius only one circle can be drawn.If radius is given and centre is not fixed then an infinite number of circles can be drawn.

52. Using only the two set-squares of the geometry box, an angle of $40^{\circ}$ can be drawn.

Ans: False.This statement is False, because we can draw only the angle by using a set square, which is divisible by 15.

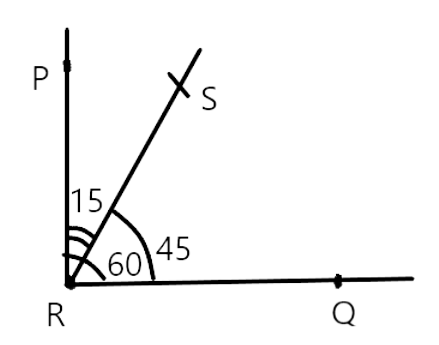
53. Using only the two set-squares of the geometry box, an angle of $15^{\circ}$ can be drawn.

Ans: True

This statement is true,

We draw a line segment $\mathrm{RQ}$ and then make $\angle P R Q=60^{\circ}$ with the help of $30^{\circ}, 60^{\circ} \& 90^{\circ}$ set square. Now, we draw another angle $\angle S R Q=45^{\circ}$ on the same side of line RQ with the help of $45^{\circ}$ and $90^{\circ}$ set square. These, we find $\angle P R S=15^{\circ}$

54. If an isosceles triangle has more than one line of symmetry, then it must be an equilateral triangle.

Ans: True .

If an isosceles triangle has no more than one line of symmetry, then it must be an equilateral triangle.

Because an equilateral triangle has three lines of symmetry and a triangle other than that cannot have two lines of symmetry.

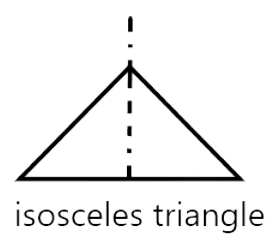
55. A square and a rectangle have the same number of lines of symmetry.

Ans: False

This statement is false. Because a rectangle has two lines of symmetry and a square has 4 lines of symmetry.

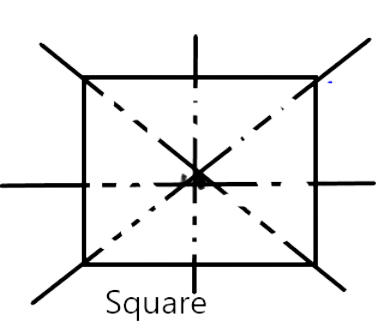
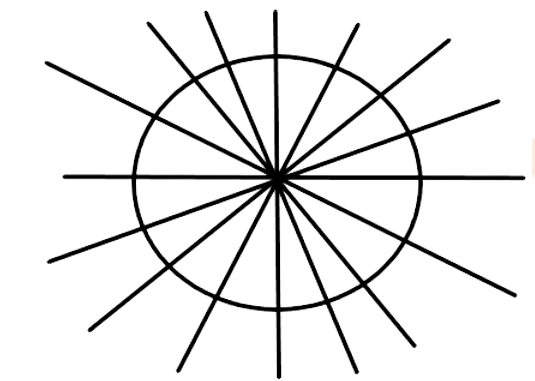
56. A circle has only 16 lines of symmetry.

Ans:False

This statement is false. Because when a circle is folded about any diameter about it, the two parts of the circle always coincide . that is why, a circle has an infinite number of lines of symmetry 

57. A $45^{\circ}-45^{\circ}-90^{\circ}$ set-square and a protractor have the same number of lines of symmetry.

Ans:True.

This statement is true. Because A $45^{\circ}-45^{\circ}-90^{\circ}$ set- square is an isosceles right-angled triangle and thus has one line of symmetry. A protector also has only one line of symmetry along the angle of $90^{\circ}$

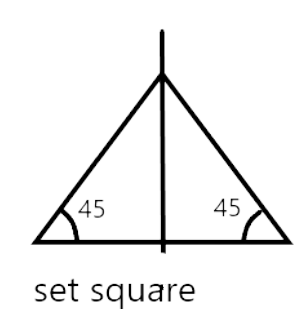
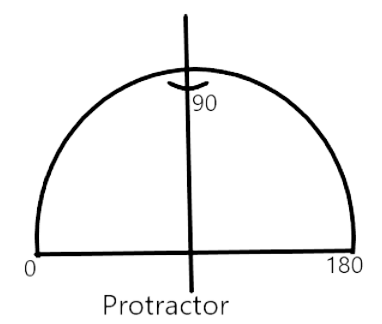
58. It is possible to draw two bisectors of a given angle.

Ans:False. This statement is False, Because only one possible bisector can be drawn at a given angle.

59. A regular octagon has 10 lines of symmetry.

Ans:False. 

This statement is false. A regular polygon with n sides has n line of symmetry and a regular octagon has 8 sides, so it has 8 line of symmetry.Four are the diagonals of regular octagon and four are the perpendicular bisectors of each pair of opposite sides.

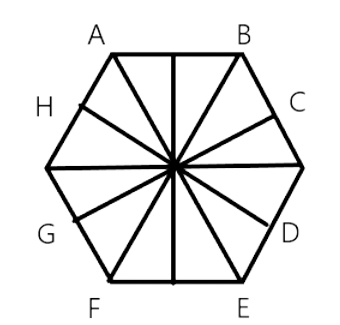
60. Infinitely many perpendiculars can be drawn to a given ray.

Ans: False. 

The given statement is False, Because, for every line segment, there is one perpendicular bisector that passes through the midpoint of the line. There are infinitely many bisectors, but only one perpendicular bisector for any segment.

61. Infinitely many perpendicular bisectors can be drawn to a given ray.

Ans: False. 

Every line segment there is one perpendicular bisector that passes through the midpoint and the other way is only when it ginter-sects a given segment at only $90^{\circ}$ angle.So given statement is false no bisectors can be draw to a given way.

62. Is there any line of symmetry in the Fig. 9.12? If yes, draw all the lines of symmetry.

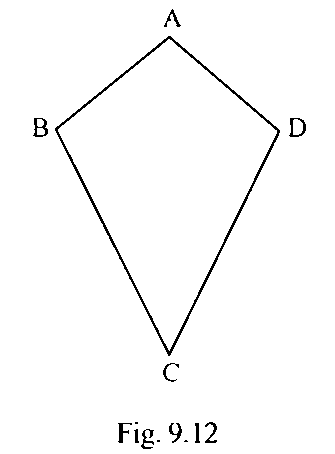
Ans: The line of symmetry divides an object in two parts and they are equal in shape and size.In the given diagram only one line of symmetry is available 

63. In Fig. 9.13, PQRS is a rectangle. State the lines of symmetry of the rectangle.

Ans:The line of symmetry divided in image and object in two parts and both are equal and copy in size, shape and length each other. 

Given diagram has two lines of symmetry because it is a rectangle. 

There are AC and DB two lines of symmetry.

64. Write all the capital letters of the English alphabets which have more than one line of symmetry.

Ans: In the English alphabet there are two types of alphabet letters one are capital alphabet letters (A,B,C) and other are small alphabet letters (a,b,c)

The line of symmetry divide an image into halves parts 

In the given question H,I,O,X are capital letters the lines of symmetry are 

65. Write the letters of the word ‘MATHEMATICS’ which have no line of symmetry

Ans: The word ‘MATHEMATICS’ is a capital letter of English alphabet 

The line of symmetry divides an object (letters, image) in two halves that are equal in shape and size.

In the ‘MATHEMATICS’ letter there is only ‘S’ has not line of  symmetry  

66. Write the number of lines of symmetry in each letter of the word ‘SYMMETRY

Ans: The word ‘SYMMETRY’ is a capital word.

It has lines of symmetry in some letters.

67. Match the following:

Ans: Lines of symmetry dissect an object from midpoint and divide it to two same shape and size parts.

Both parts are copies of each other.

68. Open your geometry box. There are some drawing tools. Observe them and complete the following table:

Ans: The lines of symmetry divides an image into two parts and both are equal in size, shape and geometrically.

69. Draw the images of points A and B in line l of Fig. 9.14 and name them as A′ and B′ respectively. Measure AB and A′ B′. Are they equal?

Ans: The length segment is always equal to their reflection because of the line of symmetry.

If AB is a line and I is the line of symmetry than the distance of line AB from line I is equal to their reflect line A’B’

70. In Fig. 9.15, the point C is the image of point A in line l and line segment BC intersects the line l at P.

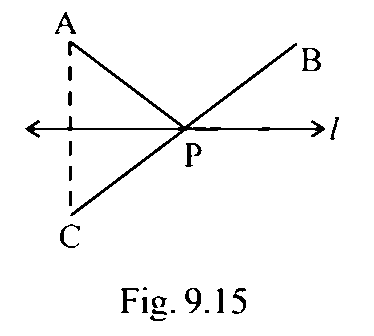
 (a) Is the image of P in line l the point P itself?

Ans: The line of symmetry divide an object or a point into same distance of their reflect a. The point ' $P$ ' is situated at line of symmetry ' $I$ 'So given statement is correct the image of $p$ in line I the point $p$ itself

 (b) Is PA = PC?

Ans: The point ' $A$ ' is situated at equal distance of line $I$ and point ' $C^{\prime}$ ' is also situated at equal distance of line I so $\mathrm{PA}=\mathrm{PC} P A=P C$

 (c) Is PA + PB = PC + PB?

Ans: Here PA=PC $P A=P C$

$\therefore P A+P B=P C+P B$

$P C+P B=P C+P B(\because P A=P C \text { We can put PA as PC) }$

$\text { Here } P B=P B$

 (d) Is P that point on line l from which the sum of the distances of points A and B is minimum?

Ans: The given statement only correct when the point ' $C$ ' $P$ and $B$ situated on line ' $I$ ' than the $\mathrm{CP}+\mathrm{PB}$ will be minimum

71. Complete the figure so that line l becomes the line of symmetry of the whole figure (Fig. 9.16).

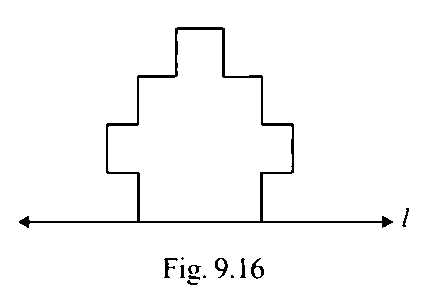
 Ans: For given solution, every point of whole diagram, should be at equal distance from line-l, and given diagram and our simulated diagram both halves would match exactly so, keeping this in mind our final complete figure will be: 

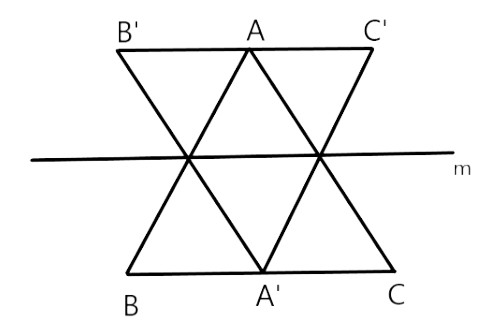
72. Draw the images of the points A, B and C in the line m (Fig. 9.17). Name them as A′, B′ and C′, respectively and join them in pairs. Measure AB, BC, CA, A′B′, B′C′ and C′A′. Is AB = A′B′, BC = B′C′ and CA = C′A′?

Ans: 

73. Draw the images P′, Q′ and R′ of the points P, Q and R, respectively in the line n (Fig. 9.18). Join P′ Q′ and Q′ R′ to form an angle P′ Q′ R′. Measure ∠PQR and ∠P′Q′R′. Are the two angles equal?

Ans: For a given situation, every point of the whole diagram should be at our equal distance from line-l, and given diagram and our simulated diagram both halves would match exactly. So, keeping this in mind our final complete figure will be:

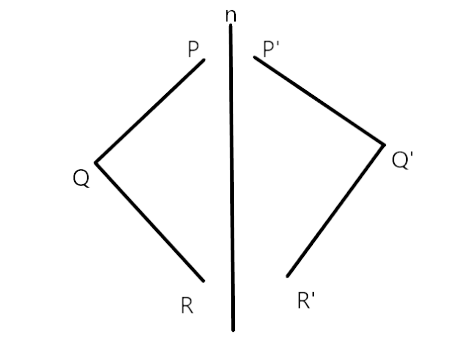
Yes, $\angle P Q R=\angle P^{\prime} Q^{\prime} R^{\prime}$ because every point of image and real diagram is at the same and opposition position so length remains the same.

$P Q=P^{\prime} Q^{\prime}$

And $Q R=Q^{\prime} R^{\prime}$

So, $\angle P Q R=\angle P^{\prime} Q^{\prime} R^{\prime}$

74. Complete Fig. 9.19 by taking l as the line of symmetry of the whole figure.

Ans: For given situation, every point of whole diagram should be at equal distance from line-l , and given diagram and our simulated diagram both halves would match exactly.

So, keeping this in mind our final complete figure will be:

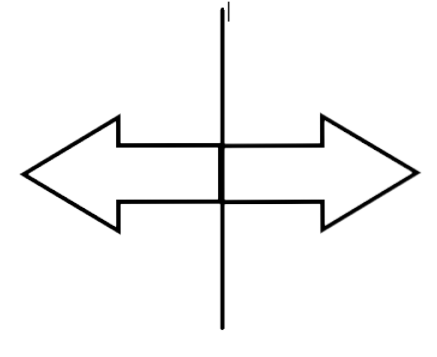
75. Draw a line segment of length 7cm. Draw its perpendicular bisector, using ruler and compasses.

Ans: Steps of construction:

Step 1: First we will draw a line segment $A B=7 \mathrm{~cm}$ with the help of a ruler.

Step 2: Then, with vertex $A$, by using compass we will take more than half of $A B$ a d draw arcs, one of each side of $A B$

Step 3: With vertex B, by using a compass with the same length we will cut the precious arcs at $X$ and $Y$ respectively.

Step 4: With the help of the ruler we will join the point $X$ and $Y$.

Thus, $X Y$ is the perpendicular bisector of line $A B$.

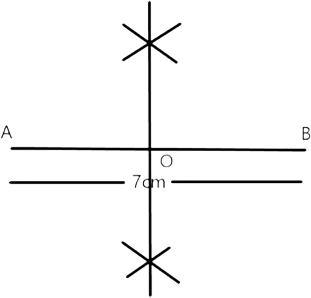
76. Draw a line segment of length 6.5 cm and divide it into four equal parts, using ruler and compasses.

Ans: Steps of construction:

Step 1: First we will draw a line segment $A B=6.5 \mathrm{~cm}$ with the help of a ruler.

Step 2: With vertex " $A$ ", by using a compass we will take more than half of $A B$ and draw arcs, one each side of $A B$.

Step 3: With vertex " $B^{\prime \prime}$, by using the same length, we will cut the previous arcs at " $E$ " and " $F^{\prime \prime}$ respectively.

Step 4: With the help of the ruler we will join the points " $\mathrm{E}$ " and " $\mathrm{F}$ " respectively.

Step 5: Thus, "Q" is the midpoint of $\mathrm{AB}(\therefore A Q=B Q)$ . Similarly, bisect the lines $\mathrm{AQ}$ and $\mathrm{BQ}$.

Thus, ' $P$ ' is the midpoint of $A Q$ and ' $R$ ', is the midpoint of $B Q$.

Now, we will divide the line segment $A B$ into four equal parts by point ' $P^{\prime}, ' Q^{\prime}$ and $R^{\prime}$.

$\therefore A P=P Q=Q R=R B$

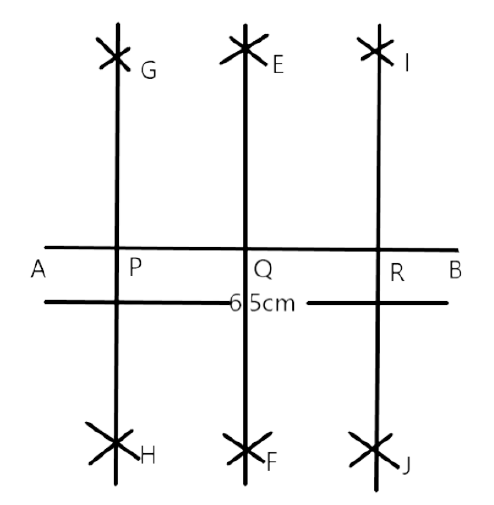
77. Draw an angle of $140^{\circ}$ with the help of a protractor and bisect it using ruler and compasses.

Ans: Steps of Construction:

Step-1: first with the help of protractor we will draw $\angle 140^{\circ}$

Step-2: We will cut $A C$ and $A B$ at $Q \& P$, Farcing past the centre and any convenient radius.

Step-3 with vertex $\mathrm{P}$, by using Compass, we will take more than half of arcs $\mathrm{PQ}$ and draw arcs.

Step-4 with vertex $\mathrm{Q}$, by using a compass with frame length, we will cut the previous area at S.

Step- 5 With the help of the ruler, we will join the point $A$ and $S$ and extend it to any point $X$.

Thus, ray $A X$ will bisect $\angle C A B$

78. Draw an angle of $65^{\circ}$ and draw an angle equal to this angle, using ruler and compasses.

Ans: Steps of construction:

Step 1: first with the help of protractor, we will draw $\angle 65^{\circ}$

Step 2: Then we will draw a ray OX.

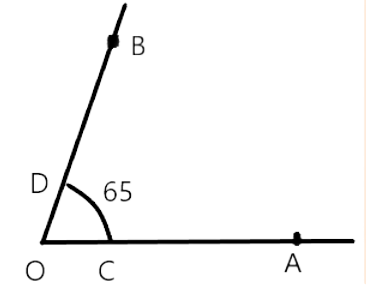
Step 3: With $\mathrm{O}$ as centre and radius, we will draw an arc cutting $\mathrm{OA}$ and $\mathrm{AB}$ at $\mathrm{C}$ and $\mathrm{D}$ respectively.

Step 4: we will draw $O^{\prime} X$ with $O^{\prime}$ as centre and with the same radius, we will draw an arc, cutting $\mathrm{O}^{\prime} \mathrm{X}$ at $\mathrm{P}$.

Step 5: With $P$ as centre and radius equal to $C D$, we will cut the $\operatorname{arcthrough~} P$ and $Q$.

Step 6: We will join $O^{\prime} Q$ and after that it produces to $Y$.

Then $\angle Y O^{\prime} X$ is the required angle equal to $\angle A O B$

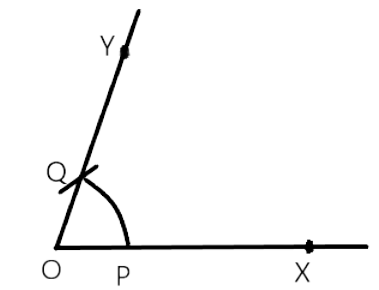
79. Draw an angle of $80^{\circ}$ using a protractor and divide it into four equal parts, using ruler and compasses. Check your construction by measurement

Ans: Steps of construction:

Step 1: First we draw an angle of $80^{\circ}\left(<80^{\circ}\right)$, with the help of a protractor.

Step 2: We will cut $O A$ and $O B$ at $Q$ and $P$, taking " $P$ " as the centre and any convenient radius.

Step 3: with vertex $P$, by using a compass we will take more than half of the arc. $P Q$ and draw arc.

Step 4: with vertex $Q$, by using a compass with the same length, we will cut the previous arc at R.

Step 5: With help of ruler we will join the point "O" and " $R$ "

$\therefore \angle A O R=\angle R O B$

Step 6: Similarly, we will bisect the arc QS and SP

$\angle A O V=\angle V O R \text { and }$

$\angle R O V=\angle V O B$

Thus, $\angle A O V, \angle V O R, \angle R O U$ and $\angle V O B$ we will divide $\angle B O A$ in four equal parts as $\angle B O A=80^{\circ}$ (given)

So, $\angle A O V=\left(\frac{80}{4}\right)^{\circ}=20^{\circ}=\angle V O R=\angle R O U=\angle V O B$

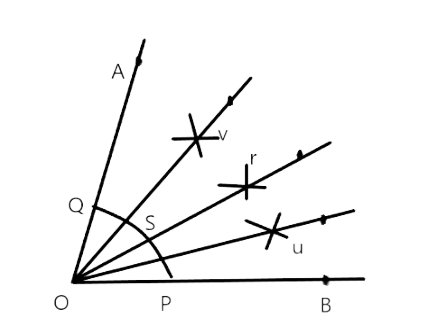
80. Copy Fig. 9.20 on your notebook and draw a perpendicular to l through P, using (i) set squares (ii) Protractor (iii) ruler and compasses. How many such perpendiculars are you able to draw?

Ans: (i) set squares 

Step 1: first we will draw a line-l and a point P on given line. Then we will rate that P is on the line –l.

Step 2: After that we will place a set square with one of its edge along the already aligned edge of ruler, such that the right angled corner is contact with the ruler.

Step 3: then slide the set square along the edge of the ruler until its right angled corner coincides with P.

Step 4: we will after these all things hold the set square in this position.

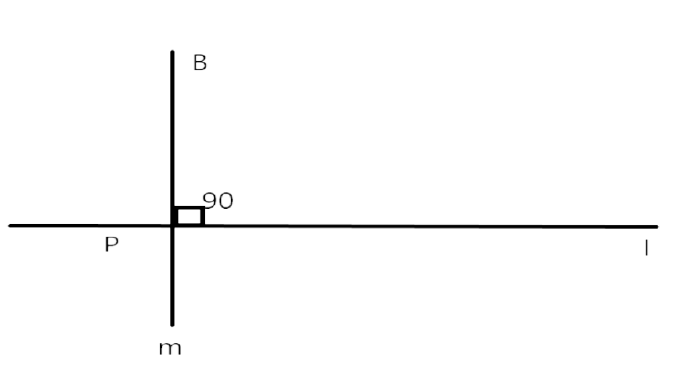
(ii) Protractor 

Step 1: first we will draw a line-l and a point P. Then we will rate that P is on the line-l.

Step 2: After that we will place the protractor on the line, such that its base line coincides with line-l and centre falls on P.

Step 3: After these all things we will mark point B again the $90^{\circ}$ mark on the protractor. Then we will draw a line-m passing through P and B , PB is our perpendicular to line-l.

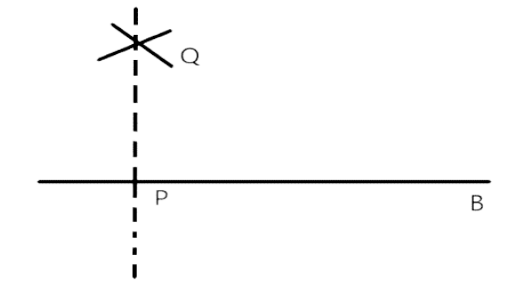
(iii) Ruler and compass:

Step 1: First we will draw a line-l on which a point-P is noted.

Step 2: After that with P as the centre and a convenient radius, construct an arc intersecting the line-l at two points A and B.

Step 3: after all these things with A and B as centre and a radius greater than AP. Construct two arcs, which cut each other at Q and join PQ and PQ is perpendicular two at line-l.

81. Copy Fig. 9.21 on your notebook and draw a perpendicular from P to line m, using (i) set squares (ii) Protractor (iii) ruler and compasses. How many such perpendiculars are you able to draw?

Ans: (i) Set square

Step 1: Place a set square with one of its edges along the already aligned with given line and the right-angled edge touches the point P.

Step 2: Then draw the line PO along the edge of the set square.

       (ii) Protractor

Step 1: For drawing perpendicularly first, place a protractor with one of its edges along the line already aligned with the given line and $90^{\circ}$ mark is along with the point P.

Step 2: Mark its centre O on line m and draw the line PO.

     (iii) Ruler and compass

Step 1: First, take P as the centre and draw an arc that cuts the line m on point A and B.

Step 2: Then take point A and B as a centre and arcs in another side with the same radius arcs cut at point Q.

Step 3: The match P and Q and PQ is perpendicular to line.

82. Draw a circle of radius 6cm using ruler and compasses. Draw one of its diameters. Draw the perpendicular bisector of this diameter. Does this perpendicular bisector contain another diameter of the circle?

Ans: 

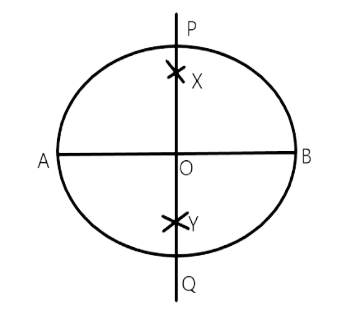
Step of construction:

1.  Draw a circle with centre 0 of radius 6cm.

2.  Now draw a diameter AB of the circle.

3.  With the centre   and radius more tham1/2(AB), draw the arcs on each side of AB.

4.  With the centre A and the same radius, draw the arcs on each side of AB which cuts the previously drawn arc at X and Y.

5.  Now join OX and OY and produce them to any point P and Q.

Thus PQ bisects the diameter of a circle. Yes, the perpendicular PQ contains another diameter of this circle.  

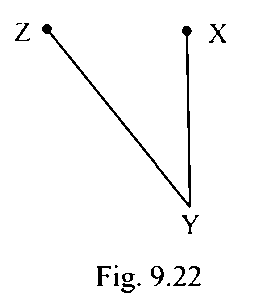
83. Bisect ∠XYZ of Fig. 9.22

Ans: 

Step 1: Firstly, draw an arc PQ, with the help of protractor.

Step 2: Now cut ZY and XY at Q and P, taking P as the centre and convenient radius.

Step 3: With vertex P, by using a compass take more than half of arc PQ and draw arc.

Step 4: With vertex Q, by using a compass with the same length, and cut the previous arc at R.

Step 5: With help of ruler join point Y and R and extend it to any point S.

Thus, ray bisect $\angle Z Y X$ $\therefore \angle Z Y S=\angle S Y X$ (YS is bisector).

84. Draw an angle of $60^{\circ}$ using ruler and compasses and divide it into four equal parts. Measure each part.

Ans:

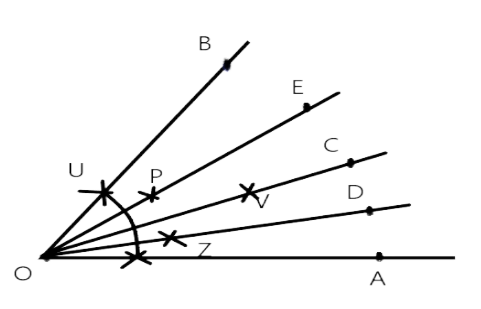
Step of contraction:

i. With the help of protractor, draw $\angle A O B=\angle 60^{\circ}$

ii. Cut $O A$ and $O B$ at $U$ and $X$, taking $O$ as the centre and any convenient radius.

iii. With vertex as centre by using compass take more than half of UX and draw an arc. iv. With vertex $u$ as centre, by using a compass with the same length cut the previous arc at $v$ and extend it to point C.

v. With point $X$ as centre by using a compass take more than half of we $W, X$ and draw an arc.

vi. With vertex $W$ are centred by using a compass with same length cut previous area at $Z$ and extend it to point D.

vii. With point $W$ as centre by using a compass take more than half of arc UW and draw an are

viii. With vertex $U$ as centre, by using a compass with the same length cut the previous arc at $P$ and extend it to point $E$.

Each part measure $=\frac{60^{\circ}}{4}=15^{\circ}$

85. Bisect a straight angle, using ruler and compasses. Measure each part.

Ans:

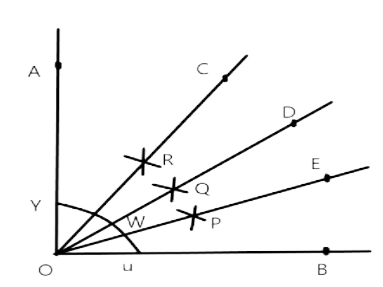
Step of construction:

1.  With the help of protractor, draw $90^{\circ}$

2.  Cut OA and OB at Y and U, taking u as the centre and any convenient radius.

3.  With vertex u, by using a compass take more than half of arc YU and draw arc.

4.  With vertex Y, by using a compass with the same length, cut the previous arc at Q and extend to point D. 

5. 
   

86. Bisect a right angle, using ruler and compasses. Measure each part. Bisect each of these parts. What will be the measure of each of these parts?

Ans: 

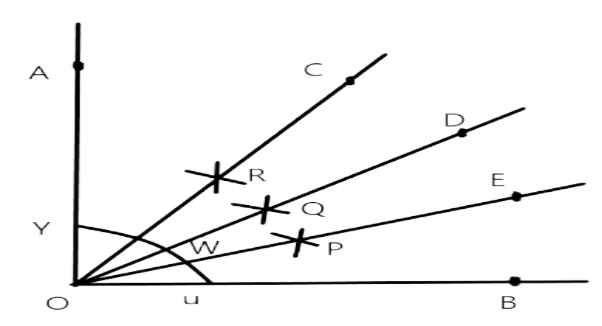
Step of construction:

i. With the help of protractor, draw $\angle 90^{\circ}$

ii. Cut $O A$ and $O B$ at $Y$ and $U$, taking $U$ as the center and any convenient radius.

iii. With vertex $U$, by using a compass take more than half of arc $\angle{C}$ and draw arc.

iv. With vertex Y, by using a compass with the same length, cut the previous arc at Q and extend to point D.

v. With help of ruler join the point $O$ and $Q$

$\therefore \angle A O D=\angle D O B$

vi. Similarly bisect the arcs $\angle{W}$ and $\angle{U}$

$\therefore \angle A O R=\angle R O \text { Dand } \angle D O E=\angle E O B$

Thus, $\angle A O R, \angle C O D, \angle D O E$ and $\angle E O B$

Divided $\angle A O B$ in four equal parts

$\therefore \angle A O R=\angle C O D=\angle D O E=\angle E O B=22 \frac{1}{2}^{\circ}$

87. Draw an angle $A B C$ of measure $45^{\circ}$, using ruler and compasses. Now draw an angle DBA of measure $30^{\circ}$ , using ruler and compasses as shown in Fig. 9.14. What is the measure of $\angle \mathrm{DBC}$ ?

Ans: 

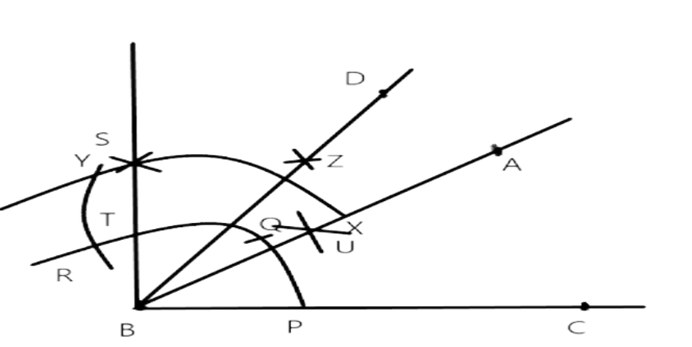
Step1. Draw a ray BC.

Step2. With B as center and any radius draw an arc which cuts BC at P.

Step3. With center P and the same radius draw on an arc which cuts the previously drawn arc at Q.

Step4. Similarly, with Q as center and same radius draw another arc which cuts a previously drawn arc at R.

Step5. With center R and O the same radius draw the arcs which cut each other at S.

Step6. Join BS which cuts the arc RP at T.

Step7. With center P and T radius more than $\frac{1}{2}(P Q)$ draw the arcs which cut each other at $\cup$.

Step8. Join BU and produce it to a point A. Thus $\angle A B C=45^{\circ}$

Step9. Now, with B as centre, draw another arc which cuts the line AB at X.

Step10. With center $X$ and the same radius drawn in step 9 at $y$.

Step11. With center $X$ an $Y$ and radius more than $\frac{1}{2}(X Y)$ draw two arcs which cut each other at $Z$.

Step12. Join BZ and produced in to a point D thus, $\angle A B D=30^{\circ}$

On measuring, we get $\angle D B C=75^{\circ}$

88. Draw a line segment of length 6cm. Construct its perpendicular bisector. Measure the two parts of the line segment.

Ans:

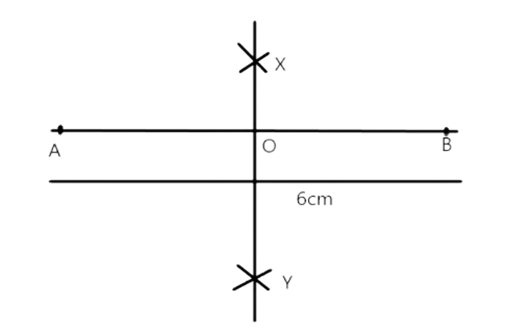
Step of construction:

i. Draw a line segment $A B=6 \mathrm{~cm}$ with the help of rules.

ii. With vertex A, by using a compass take more than half of AB and draw arcs, one cash side at sides of $A B$.

iii. With vertex B, by using a compass with the same length, cut the previous arcs at X and Y respectively.

iv. With the help of the ruler join the points $X$ and $Y$.

Thus, $X Y$ is the perpendicular bisector of line $A B$.

On measuring the two parts we get $A O=O B=3 \mathrm{~cm}$.

89. Draw a line segment of length 10cm. Divide it into four equal parts. Measure each of these parts.

Ans:

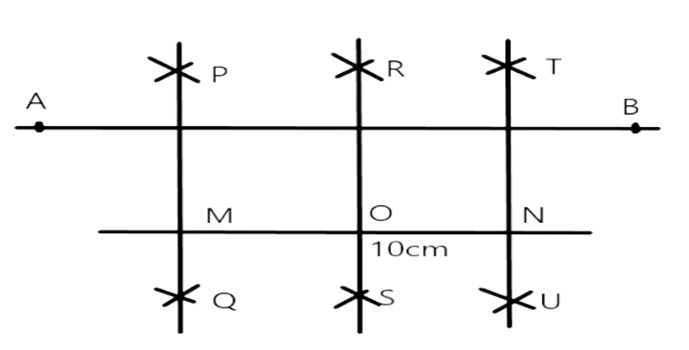
Step of construction:

(i).  Draw a line segment $A B=10 \mathrm{~cm}$ with the help of ruler.

(ii). With vertex A. by using compass take more than help half of AB and draw arcs at R and S respectively

(iii). With vertex $B$, by using a compass with the same length, cut the previous arcs at $R$ and $S$ respectively.

(iv). With help of ruler join the point $R$ and $S$, thus $O$ is midpoint of $A B(\therefore A O=B O)$

(v). Similarly bisect the lines AO and BO thus $m$ is mid-point of AO and N, is mid-point at BO.

Now, points $M, O$ and $N$ divided the line segment $A B$ in points

$\therefore A M=M O=O N=N B=2.5 \mathrm{~cm}$

About The Chapter

Practical Geometry, the final Chapter of CBSE Class 6 Math, deals with the creation of the shapes that the students are already familiar with, as well as the instruments that are used in the process of generating the shapes. The topics covered in this Chapter include the circle, the construction of a circle when its radius is known, a line segment, the construction of a line segment of a given length, the construction of a copy of a given line segment, the construction of a line segment through a point on it,  perpendiculars, angles, the construction of an angle of a given measure, the construction of a copy of an angle of unknown measure.