NCERT Exemplar for Class 6 Maths Solutions Chapter 8 Ratio & Proportion

Solved examples

In examples 1 and 2, write the correct answer from the given four options: 

Example 1: The ratio of Rs 8 to 80 paise is 

(A) 1: 10 

(B) 10: 1 

(C) 1: 1 

(D) 100: 1 

Ans: Option (B) is the correct answer.

1 rupee = 100 paise

So, Rs 8 = 800paise

$\Rightarrow Ratio=\dfrac{Rs.8}{80 paise}=\dfrac{800\text{ paise}}{80 \text{paise}}=\dfrac{10}{1}$

Thus correct answer is option (B)

Example 2: The length and breadth of a steel tape are 10m and 2.4cm, respectively. The ratio of the length to the breadth is 

(A) 5: 1.2 

(B) 25: 6 

(C) 625: 6 

(D) 1250: 3 

Ans: Option (D) is the correct answer.

1 mètre = 100 cm

So, 10m = 100 cm

$\Rightarrow Ratio=\dfrac{10m}{2.4cm}=\dfrac{1000cm}{2.4cm}=\dfrac{1250}{3}$

Thus correct answer is option (D) 

Example 3: Find the missing number in the box in the following proportion: $\square$  : 8 :: 12 : 32 .

Ans: \[\dfrac{12}{32}=\dfrac{3\times 4}{8\times 4}=\dfrac{3}{8}\]

Thus, the missing number in place of the box is 3.

Example 4: State whether the given statements are true or false: 

(a) 12 : 18 = 28 : 56 

Ans: $\dfrac{12}{18}=\dfrac{2\times 6}{3\times 6}=\dfrac{2}{3}$ and $\dfrac{28}{56}=\dfrac{28\times 1}{28\times 2}=\dfrac{1}{2}$

$\dfrac{2}{3}\ne \dfrac{1}{3}$

$\dfrac{12}{18}\ne \dfrac{28}{56}$

The statement is false.

(b) 25 persons : 130 persons = 15kg : 78kg 

Ans: $\dfrac{25 \text{persons}}{130 \text{persons}}=\dfrac{5\times 5}{5\times 26}=\dfrac{5}{26}$ and $\dfrac{15kg}{78kg}=\dfrac{5\times 3}{26\times 3}=\dfrac{5}{26}$

$\therefore \dfrac{25 persons}{130 persons}=\dfrac{15kg}{78kg}$

The statement is true.

Example 5: Fill in the blanks: If two ratios are ______, then they are in proportion. 

Ans: For the ratios to be in proportion they have to be equal.

So, the correct answer is: If two ratios are equal then they are in proportion.

Example 6: Find the ratio of the shaded portion to the unshaded portion in Fig. 8.1 

Ans: No. of square in the shaded region = 15

No. of square in the unshaded region = 33

$\Rightarrow Ratio=\dfrac{\text{No. of squares in the shaded region}}{\text{No. of squares in the unshaded region}}=\dfrac{15}{33}=\dfrac{5}{11}$

Ratio of shaded part to unshaded part = 5: 11.

Example 7: Income of Rahim is Rs 12000 per month and that of Ami is Rs 191520 per annum. If the monthly expenditure of each of them is Rs 9960 per month, find the ratio of their savings. 

Ans: Rahim’s income = Rs. 12,000/month and Monthly expenditure = Rs. 9960/month.

So, Rahim’s savings = Rahim’s income - Monthly expenditure

= Rs. 12,000 - Rs. 9960

= Rs 2040

Ami’s annual income = Rs 1,91,520

Ami’s Monthly income = $\dfrac{Rs.191520}{12}=Rs.15960$

Monthly expenditure = Rs. 9960/month.

So, Ami’s savings = Ami’s income - Monthly expenditure

= Rs. 15,960 - Rs. 9960

= Rs 6000

$Ratio=\dfrac{\text{Rahim’s savings}}{\text{Ami's savings}}=\dfrac{Rs.2040}{Rs.6000}=\dfrac{17}{50}$

Example 8: 20 tons of iron costs Rs 600000. Find the cost of 560kg of iron. 

Ans: 1 ton = 1000 kg

So, 20 ton = 20000 kg.

Let the cost of 540kg iron be x.

$\therefore \dfrac{20000kg}{Rs.600000}=\dfrac{560kg}{Rs.x}$

$Rs.x=\dfrac{Rs.600000\times 560kg}{20000kg}=Rs.16800$

Cost of 560kg of iron = Rs. 16800

Exercise

In questions 1 to 10, only one of the four options is correct. Write the correct one.

1. The ratio of 8 books to 20 books is

(A) 2: 5

(B) 5: 2

(C) 4: 5

(D) 5: 4

Ans:  Option (A) is the correct answer.

$\text{Ratio of 8 books to 20 books}=\dfrac{8}{20}=\dfrac{2}{5}$

2. The ratio of the number of sides of a square to the number of edges of a cube is

(A) 1: 2

(B) 3: 2

(C) 4: 1

(D) 1: 3

Ans: Option (D) is the correct answer.

Number of sides of a square = 4

Edges of a cube = 12

$Ratio\text{=}\dfrac{\text{No. of sides taken in square}}{\text{No. of edges in cube}}=\dfrac{4}{12}=\dfrac{1}{3}$

3. The picture is 60cm wide and 1.8m long. The ratio of its width to its perimeter in lowest form is

(A) 1: 2

(B) 1: 3

(C) 1: 4

(D) 1: 8

Ans: Option (D) is the correct answer.

Width of picture = 60 cm = 0.6m

Length of picture = 1.8 m

\[Perimeter = 2 \times \left( {length + width} \right)\]

$ = 2\left( {0.6 + 1.8} \right) = 2\left( {2.4} \right) = 4.8m$

$\text{Ratio} = \dfrac{\text{Width}}{\text{Perimeter}} = \dfrac{{0.6m}}{{4.8m}} = \dfrac{1}{8}$

4. Neelam’s annual income is Rs. 288000. Her annual savings amount to Rs. 36000. The ratio of her savings to her expenditure is

(A) 1: 8

(B) 1: 7

(C) 1: 6

(D) 1: 5

Ans: Option (B) is the correct answer.

Neelam’s,

Annual income = Rs. 288000

Annual savings amount = Rs. 36000

$\therefore \text{Annual expenditure} =\text{Annual income-Annual savings amount}$

$ = Rs.{\text{ }}288000 - Rs.{\text{ }}36000 = Rs.{\text{ }}2,52,000$

$\text{Ratio}=\dfrac{\text{Annual savings amount}}{\text{Annual expenditure}}=\dfrac{Rs.\text{ }36000}{Rs.\text{ 2,52,000}}\text{=}\dfrac{1}{7}$

5. The Mathematics textbook for Class VI has 320 pages. The chapter ‘symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is

(A) 11: 320

(B) 3: 40

(C) 3: 80

(D) 272: 320

Ans: Option (C) is the correct answer.

Total no. of pages in the book = 320

Total number of pages in ‘symmetry’ chapter = 12

\[\dfrac{\text{Total no. of pages in symmetry chapter}}{\text{Total no. of pages in the book}}=\dfrac{12}{320}=\dfrac{3}{8}\] 

6. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?

(A) 18

(B) 19

(C) 21

(D) 22

Ans: Option (D) is the correct answer.

Ratio of red marbles to blue marbles is 7:4.

Thus, No. of red marbles = 7x

No. of blue marbles = 4x

Sum of ratio of Total no. of marbles = 11x.

So, the total no. of marbles should be divisible by 11. Thus, 22 is the correct answer.

7. On a shelf, books with a green cover and that with brown cover are in the ratio 2:3. If there are 18 books with a green cover, then the number of books with brown cover is

(A) 12

(B) 24

(C) 27

(D) 36

Ans: Option (C) is the correct answer.

Ratio of green cover books: Brown cover books = 2:3

No. of green cover books = 18

Let the No. of brown cover books = x

\[\dfrac{\text{No. of Green cover books}}{\text{No. of Brown cover books}}=\dfrac{2}{3}\]

\[\Rightarrow \dfrac{18}{x}=\dfrac{2}{3}\]

$2x=18\times 3$

$x=\dfrac{54}{2}=27$

No. of brown cover books = 27

8. The greatest ratio among the ratios 2: 3, 5: 8, 75: 121 and 40: 25 is

(A) 2: 3

(B) 5: 8

(C) 75: 121

(D) 40: 25

Ans: Option (D) is the correct answer.

The four ratios are:

$\dfrac{2}{3},\dfrac{5}{8},\dfrac{{75}}{{121}},\dfrac{{40}}{{25}}$

Let’s take the LCM of their denominators.

Thus, the LCM of 3, 8, 121 and 25 = \[2 \times 2 \times 2 \times 3 \times 5 \times 5 \times 11 \times 11 = 72600\]

Now, make all the denominators equal to 72600

\[\dfrac{2}{3} = \dfrac{{2 \times 24200}}{{3 \times 24200}} = \dfrac{{48400}}{{72600}}\]

\[\dfrac{5}{8} = \dfrac{{5 \times 9075}}{{8 \times 9075}} = \dfrac{{45375}}{{72600}}\]

\[\dfrac{{75}}{{121}} = \dfrac{{75 \times 600}}{{121 \times 600}} = \dfrac{{45000}}{{72600}}\]

\[\dfrac{{40}}{{25}} = \dfrac{{40 \times 2904}}{{25 \times 2904}} = \dfrac{{116160}}{{72600}}\]

Comparing all the ratios,

\[\dfrac{{116160}}{{72600}}\] is the biggest.

Therefore, \[\dfrac{{40}}{{25}}\] is the greatest ratio.

9. There are ‘b’ boys and ‘g’ girls in a class. The ratio of the number of boys to the total number of students in the class is:

(A) \[\dfrac{{\mathbf{b}}}{{{\mathbf{b}} + {\mathbf{g}}}}\]

(B) $\dfrac{{\mathbf{g}}}{{{\mathbf{b}} + {\mathbf{g}}}}$

(C) $\dfrac{{\mathbf{b}}}{{\mathbf{g}}}$

(D) $\dfrac{{{\mathbf{b}} + {\mathbf{g}}}}{{\mathbf{b}}}$

Ans: Option (A) is the correct answer.

Total no. of boys is represented by ‘b’ and girls by ‘g’ respectively.

Total no. of students = b + g

$\Rightarrow \text{Ratio}=\dfrac{\text{Total no. of boys}}{\text{Total no. of students}}=\dfrac{b}{b+g}$ 

10. If a bus travels 160 km in 4 hours and a train travels 320km in 5 hours at uniform speeds, then the ratio of the distances travelled by them in one hour is

(A) 1: 2

(B) 4: 5

(C) 5: 8

(D) 8: 5

Ans: Option (C) is the correct answer.

Bus travels 160 km in 4 hours.

So, Bus travels  $\dfrac{{160}}{4} = 40km$ in 1 hour.

Similarly, a train travels 320km in 5 hours. So, trains travel $\dfrac{{320}}{5} = 64km$ in 1 hour.

Ratio of the distances travelled by bus and train in 1 hour = $\dfrac{{40}}{{64}} = \dfrac{5}{8}$

In questions 11 to 15, find the missing number in the box in each of the proportions:

11. Find the number in place of the question mark: $\dfrac{3}{5} = \dfrac{?}{{20}}$

Ans: Let the number at the question mark's place be x.

$\dfrac{3}{5} = \dfrac{x}{{20}}$

Now, cross multiply 5 by x and 3 by 20.

$3 \times 20 = 5 \times x$

$\Rightarrow x = \dfrac{{3 \times 20}}{5} = 3 \times 4 = 12$

\[\therefore x = 12\]

12. Find the number in place of the question mark: $\dfrac{?}{{18}} = \dfrac{2}{9}$

Ans: Let the number at the question mark's place be x.

$\dfrac{x}{{18}} = \dfrac{2}{9}$

Now, cross multiply 9 by x and 18 by 2.

$18 \times 2 = 9 \times x$

$\Rightarrow x = \dfrac{{18 \times 2}}{9} = 2 \times 2 = 4$

\[\therefore x = 4\]

13. Find the number in place of the question mark: $\dfrac{8}{?} = \dfrac{{3.2}}{4}$

Ans: Let the number at the question mark's place be x.

$\dfrac{8}{x} = \dfrac{{3.2}}{4}$

Now, cross multiply 3.2 by x and 8 by 4.

$8 \times 4 = 3.2 \times x$

$\Rightarrow x = \dfrac{{8 \times 4}}{{3.2}} = 10$

\[\therefore x = 10\]

14. Find the number in place of the question mark: $\dfrac{?}{{45}} = \dfrac{{16}}{{40}} = \dfrac{{24}}{?}$

Ans: Let the numbers at the question marks place be x1 and x2

$\dfrac{{{x_1}}}{{45}} = \dfrac{{16}}{{40}} = \dfrac{{24}}{{{x_2}}}$

First, we will calculate ${x_1}$ using the first two ratios.

$\dfrac{{{x_1}}}{{45}} = \dfrac{{16}}{{40}}$

Now, cross multiply 40 by ${x_1}$ and 16 by 45.

$16 \times 45 = 40 \times {x_1}$

$\Rightarrow {x_1} = \dfrac{{16 \times 45}}{{40}} = 18$

\[\therefore {x_1} = 18\]

Let’s calculate \[{x_2}\] the other two ratios,

$\dfrac{{16}}{{40}} = \dfrac{{24}}{{{x_2}}}$

$\Rightarrow 16 \times {x_2} = 40 \times 24$

${x_2} = \dfrac{{40 \times 24}}{{16}} = 60$

\[\therefore {x_2} = 60\]

15. Find the number in place of the question mark: \[\dfrac{{16}}{{36}} = \dfrac{?}{{63}} = \dfrac{{36}}{?} = \dfrac{?}{{117}}\]

Ans: Let the numbers at the question marks place be x1, x2 and x3

$\dfrac{{16}}{{36}} = \dfrac{{{x_1}}}{{63}} = \dfrac{{36}}{{{x_2}}} = \dfrac{{{x_3}}}{{117}}$

First, we will calculate ${x_1}$ using the first two ratios.

$\dfrac{{16}}{{36}} = \dfrac{{{x_1}}}{{63}}$

Now, cross multiply 36 by ${x_1}$ and 16 by 63.

$16 \times 63 = {x_1} \times 36$

$\Rightarrow {x_1} = \dfrac{{16 \times 63}}{{36}} = 28$

\[\therefore {x_1} = 28\]

Let’s calculate \[{x_2}\] the other two ratios,

$\dfrac{{28}}{{63}} = \dfrac{{36}}{{{x_2}}}$

$\Rightarrow 28 \times {x_2} = 36 \times 63$

$\Rightarrow {x_2} = \dfrac{{36 \times 63}}{{28}} = 81$

\[\therefore {x_2} = 81\]

Finally, let’s calculate x3

$\dfrac{{36}}{{81}} = \dfrac{{{x_3}}}{{117}}$

$\Rightarrow 81 \times {x_3} = 36 \times 117$

$\Rightarrow {x_3} = \dfrac{{36 \times 117}}{{81}} = 52$

\[\therefore {x_3} = 52\]

In questions 16 to 34, state whether the given statements are true (T) or false (F).

16. State if the proportion is true or false: $\dfrac{{\mathbf{3}}}{{\mathbf{8}}} = \dfrac{{15}}{{{\mathbf{40}}}}$

Ans: The given ratio is True.

If we multiply $\dfrac{3}{8}$ by 5 we get $\dfrac{{15}}{{40}}$

$ \Rightarrow \dfrac{{3 \times 5}}{{8 \times 5}} = \dfrac{{15}}{{40}}$

$\therefore \dfrac{3}{8} = \dfrac{{15}}{{40}}$

17. State if the ratio is true or false: 4: 7 = 20: 35

Ans: The given ratio is True.

If we multiply $\dfrac{4}{7}$ by 5 we get $\dfrac{{20}}{{35}}$

$ \Rightarrow \dfrac{{4 \times 5}}{{7 \times 5}} = \dfrac{{20}}{{35}}$

$\therefore 4:7=20:35$

18. State if the ratio is true or false: 0.2: 5 = 2: 0.5

Ans: The given ratio is False.

If we multiply $\dfrac{{0.2}}{5}$ by 10 we get $\dfrac{2}{{50}}$

$ \Rightarrow \dfrac{{0.2 \times 10}}{{5 \times 10}} = \dfrac{2}{{50}} \ne \dfrac{2}{{0.5}}$

$\therefore 0.2:5\ne 2:0.5$

19. State if the ratio is true or false: 3: 33 = 33: 333

Ans: The given ratio is False.

If we multiply $\dfrac{3}{{33}}$ by 11 we get $\dfrac{{33}}{{363}}$

\[ \Rightarrow \dfrac{{3 \times 11}}{{33 \times 11}} = \dfrac{{33}}{{363}} \ne \dfrac{{33}}{{333}}\]

$\therefore 3:33 \ne 33:333$

20. State if the ratio is true or false: 15m: 40m = 35m: 65m

Ans: The given ratio is False.

If we multiply $\dfrac{{15}}{{40}}$ by 16.24 we get $\dfrac{{24.375}}{{60}}$

$ \Rightarrow \dfrac{{3 \times 16.24}}{{8 \times 16.24}} = \dfrac{{24.375}}{{60}}$

$\therefore 15m:40m\ne 35m:65m$

21. State if the ratio is true or false: 27 ${\mathbf{c}}{{\mathbf{m}}^{\mathbf{2}}}$ : 57 ${\mathbf{c}}{{\mathbf{m}}^{\mathbf{2}}}$ = 18cm : 38cm

Ans: The given ratio is True.

If we multiply $\dfrac{{18}}{{38}}$ by 1.5 we get $\dfrac{{27}}{{57}}$

$ \Rightarrow \dfrac{{18 \times 1.5}}{{38 \times 1.5}} = \dfrac{{27}}{{57}}$

$\therefore 27c{{m}^{2}}:57c{{m}^{2}}=18cm:38cm$

22. State if the ratio is true or false: 5kg: 7.5kg = Rs 7.50: Rs 5

Ans: The given ratio is False.

If we multiply $\dfrac{5}{{7.5}}$ by 1.5 we get $\dfrac{{7.5}}{{11.25}}$

$ \Rightarrow \dfrac{{5 \times 1.5}}{{7.5 \times 1.5}} = \dfrac{{7.5}}{{11.25}}$

$\therefore 5kg:7.5kg\ne Rs7.50:Rs5$

23. State if the ratio is true or false: 20g: 100g = 1metre: 500cm

Ans: The given ratio is True.

If we multiply $\dfrac{{20}}{{100}}$ by 5 we get $\dfrac{{100cm}}{{500cm}} = \dfrac{{1m}}{{500cm}}$

$ \Rightarrow \dfrac{{20g}}{{100g}} \times \dfrac{5}{5} = \dfrac{{100cm}}{{500cm}} = \dfrac{{1m}}{{500cm}}$

$\therefore 20g:100g=1metre:500cm$

24. State if the statement is true or false: 12 hours: 30 hours = 8km: 20km

Ans: The given ratio is True.

If we multiply $\dfrac{8}{{20}}$ by 1.5 we get $\dfrac{{12}}{{30}}$

$ \Rightarrow \dfrac{{8 \times 1.5}}{{20 \times 1.5}} = \dfrac{{12}}{{30}}$

$\therefore 12hours:30hours=8km:20km$

25. State if the statement is true or false: The ratio of 10kg to 100kg is 1:10

Ans: The given ratio is True.

$\Rightarrow \dfrac{10kg}{100kg}=\dfrac{1}{10}$

$\therefore $ The ratio of 10kg to 100kg is 1: 10.

26. State if the statement is true or false: The ratio of 150cm to 1metre is 1:1.5.

Ans: The given statement is False.

If we divide $\dfrac{{150cm}}{{1m}}$ by 100 we get $\dfrac{{1.5}}{1}$

$ \Rightarrow \dfrac{{150cm}}{{1m}} = \dfrac{{150cm \div 100}}{{100cm \div 100}} = \dfrac{{1.5}}{1}$

$\therefore $ The ratio of 150 cm to 1 metre is 1: 15.

27. State if the ratio is true or false: 25kg: 20g = 50kg: 40g

Ans: The given ratio is True

If we multiply $\dfrac{25}{20}$ by 2 we get $\dfrac{50}{40}$

$\Rightarrow \dfrac{25\times 2}{20\times 2}=\dfrac{50}{40}$

$\therefore 25kg:20g=50kg:40g$

28. State if the statement is true or false: The ratio of 1 hour to one day is 1:1.

Ans: The given statement is False

1 day = 24 hours.

$ \Rightarrow \dfrac{{1hour}}{{1day}} = \dfrac{{1hr}}{{24hr}} = \dfrac{1}{{24}}$

29. State if the statement is true or false: Ratio 4: 16 is in its lowest form.

Ans: The given statement is False

$ \Rightarrow \dfrac{4}{{16}} = \dfrac{{4 \div 4}}{{16 \div 4}} = \dfrac{1}{4}$

30. State if the statement is true or false: The ratio 5: 4 is different from the ratio 4: 5.

Ans: The given statement is True

The ratio 5: 4 is the reciprocal of 4: 5. So they are different ratios.

31. State if the statement is true or false: A ratio will always be more than 1.

Ans: The given statement is False

If the denominator of the ratio is more than the numerator, then the ratio will be less than 1.

$\therefore $ A ratio can be less than 1.

32. State if the statement is true or false: A ratio can be equal to 1.

Ans: The given statement is True

If both the numerator and the denominator are the same then the ratio can be equal to 1.

33. State if the statement is true or false: If b: a = c: d, then a, b, c, d is in proportion.

Ans: The given statement is False

$\therefore $  If a: b = c: d, then a, b, c, d is said to be in proportion.

34. State if the statement is true or false: The two terms of a ratio can be in two different units.

Ans: The given statement is False.

In questions 35 to 46, fill in the blanks to make the statements true.

35. A ratio is a form of comparison by ______.

Ans: A ratio is a form of comparison by division.

36. Complete the blank: 20m: 70m = Rs 8: Rs ______.

Ans: $\dfrac{20m}{70m}=\dfrac{Rs.\text{ 8}}{x}$

37. There is a number in the box $ \square $ such that $\square $, 24, 9, 12 are in proportion. The number in the box is _____.

Ans: Let the number in the box be x.

$ \square $, 24, 9, and 12 are in proportion.

$\therefore  [\kern-0.15em[ x ]\kern-0.15em] :24::9:12$

$\therefore \dfrac{{ [\kern-0.15em[ x ]\kern-0.15em] }}{{24}} = \dfrac{9}{{12}}$

$ [\kern-0.15em[ x ]\kern-0.15em]  = \dfrac{{9 \times 24}}{{12}} = 18$

Therefore, the number in the box is 18.

$x = \dfrac{{70 \times 8}}{{20}} = 28$

$\therefore $ 20m: 70m = Rs. 8: Rs 28

38. If two ratios are equal, then they are in  _____.

Ans: If two ratios are equal, then they are in proportion.

Use Fig. 8.2. (In which each square is of unit length) for questions 39 and 40:

39. The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is _______.

Ans: length of each side of square = 1 unit.

Boundary of shaded portion = 6 units

Boundary of the whole figure = (4+4+3+3) = 14 units

\[\dfrac{\text{Perimeter of boundary of shaded portion}}{\text{Perimeter of boundary of the whole figure}}=\dfrac{6}{14}=\dfrac{3}{7}\]

The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is 3: 7.

40. The ratio of the area of the shaded portion to that of the whole figure is ______.

Ans: length of each side of square = 1 unit.

Length of the shaded part = 2 units and breadth of the shaded part = 1 unit.

$\text{Area of shaded part} = (l \times b)=(2\times 1)=2uni{{t}^{2}}$

Also, Length of the whole figure = 4 units and breadth of the whole figure = 3 units.

$\text{Area of whole figure} = ({l}\times b)=(4\times 3)=12uni{{t}^{2}}$

\[\therefore \text{Ratio}=\dfrac{\text{Area of the shaded portion}}{\text{Area of the whole figure}}=\dfrac{2}{12}=\dfrac{1}{6}\]

The ratio of the area of the shaded portion to that of the whole figure is 1:6.

41. Sleeping time of a python in a 24-hour clock is represented by the shaded portion in Fig. 8.3. The ratio of sleeping time to awaking time is ______.

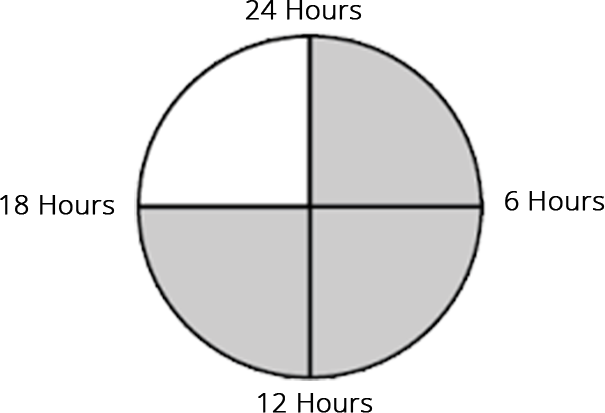
Ans: According to the figure,

Python sleeps for = 18 hours

Python is awake for = 24 – 18 = 6 hours.

$Ratio=\dfrac{\text{Sleeping time}}{\text{Awaking time}}=\dfrac{18}{6}=\dfrac{3}{1}$

The ratio of sleeping time to waking time is 3: 1.

42. A ratio expressed in lowest form has no common factor other than ______ in its terms. 

Ans: All numbers have 1 as their common factor.

Thus, a ratio expressed in lowest form has no common factor other than one in its terms. 

43. To find the ratio of two quantities, they must be expressed in _____units. 

Ans: Two quantities in the ratio must have the same unit.

Thus, to find the ratio of two quantities, they must be expressed in similar units. 

44. The ratio of 5 paisa to 25 paisa is the same as the ratio of 20 paise to _____ 

Ans: Let the missing paisa be x 

$\dfrac{{5p}}{{25p}} = \dfrac{{20p}}{x}$

To convert 5p into 20p we will multiply the former by 4. Similarly, the denominator 25p will also be multiplied by 4.

So, we get

$\dfrac{{5p}}{{25p}} \times \dfrac{4}{4} = \dfrac{{20p}}{{100p}}$

$\therefore \dfrac{{5p}}{{25p}} = \dfrac{{20p}}{{100p}}$

The ratio of 5 paisa to 25 paisa is the same as the ratio of 20 paise to 100 paisa.

45. Saturn and Jupiter take 9 hours 56 minutes and 10 hours 40 minutes, respectively for one spin on their axes. The ratio of the time taken by Saturn and Jupiter in the lowest form is ______. 

Ans: We will convert the time given in hours and minutes into minutes only.

\[\text{Time taken by Saturn}=9hour 56min=9\times 60min+56min=\left( 540+56 \right)min=596min\]

\[\text{Time taken by Jupiter}=10hour 40min=10\times 60\text{ }min+40\text{ }min=\left( 600+40 \right)min=640min\]

\[Ratio=\dfrac{\text{Time taken by Saturn}}{\text{Time taken by Jupiter}}=\dfrac{596}{640}=\dfrac{149}{160}\]

The ratio of the time taken by Saturn and Jupiter in the lowest form is 149:160. 

46. 10g of caustic soda dissolved in 100mL of water makes a solution of caustic soda. The amount of caustic soda needed for 1 litre of water to make the same type of solution is ______. 

Ans: Let the amount of caustic soda needed for 1 litre of water be x.

$\therefore \dfrac{{10gm}}{{100ml}} = \dfrac{x}{{1 litre}}$

We know that 1 litre = 1000ml.

$\therefore \dfrac{{10gm}}{{100ml}} = \dfrac{x}{{1000ml}}$

So to convert 100ml into 1 lire (1000ml), we will cross multiply the denominator 100ml by x. Similarly, the numerator 10gm will also be multiplied by 1000.

$\therefore 10gm \times 1000ml = x \times 100ml$

$x = \dfrac{{10gm \times 1000ml}}{{100ml}} = 100gm$

Amount of caustic soda = 100gm.

Thus, 10g of caustic soda dissolved in 100mL of water makes a solution of caustic soda. The amount of caustic soda needed for 1 litre of water to make the same type of solution is 100gm.

47. The market price of a table is Rs 625 and its sale price is Rs 500. What is the ratio of the sale price to the market price?

Ans: Given:

The market price of the table = Rs. 625 

The sale price of the table = Rs. 500

$Ratio=\dfrac{\text{Sale price of table}}{\text{Market price of table}}=\dfrac{Rs. 500}{Rs. \text{625}}=\dfrac{4}{5}$

The sale price ratio to the market price = 4: 5.

48. Which pair of ratios are equal? And why?

(i). $\dfrac{{\mathbf{2}}}{{\mathbf{3}}},\dfrac{{\mathbf{4}}}{{\mathbf{6}}}$.

Ans: $\dfrac{2}{3},\dfrac{4}{6}$

This pair of ratios are equal because if you multiply $\dfrac{2}{3}$ by 2, we get $\dfrac{4}{6}$ .

$ \Rightarrow \dfrac{2}{3} \times \dfrac{2}{2} = \dfrac{4}{6}$

$\therefore \dfrac{2}{3} = \dfrac{4}{6}$

(ii). $\dfrac{{\mathbf{8}}}{{\mathbf{4}}},\dfrac{{\mathbf{2}}}{{\mathbf{1}}}$.

Ans: $\dfrac{8}{4},\dfrac{2}{1}$

This pair of ratios are equal because if we divide $\dfrac{8}{4}$ by 4, we get $\dfrac{2}{1}$ .

$ \Rightarrow \dfrac{{8 \div 4}}{{4 \div 4}} = \dfrac{2}{1}$

$\therefore \dfrac{8}{4} = \dfrac{2}{1}$

(iii). $\dfrac{{\mathbf{4}}}{{\mathbf{5}}},\dfrac{{{\mathbf{12}}}}{{{\mathbf{20}}}}$.

Ans: $\dfrac{4}{5},\dfrac{{12}}{{20}}$

The above ratio is not equal because, if you multiply $\dfrac{4}{5}$ by 3, we get $\dfrac{{12}}{{15}}$ .

\[ \Rightarrow \dfrac{4}{5} \times \dfrac{3}{3} = \dfrac{{12}}{{15}} \ne \dfrac{{12}}{{20}}\]

$\dfrac{4}{5} \ne \dfrac{{12}}{{20}}$

49. Which ratio is larger 10: 21 or 21: 93?

Ans: Firstly, we will have to equalise the numerator of both ratios.

So, we will multiply the first ratio $\dfrac{{10}}{{21}}$ by 2.1.

$\dfrac{{10 \times 2.1}}{{21 \times 2.1}} = \dfrac{{21}}{{44.1}}$

And the second ratio is $\dfrac{{21}}{{93}}$

As the denominator of the first ratio is smaller, the first ratio is greater than the second ratio.

$\dfrac{{21}}{{44.1}} > \dfrac{{21}}{{93}}$

$\therefore \dfrac{{10}}{{21}} > \dfrac{{21}}{{93}}$

50. Reshma prepared 18kg of Burfi by mixing Khoya with sugar in the ratio of 7: 2. How much Khoya did she use?

Ans: Reshma mixed Khoya and sugar in the ratio 7: 2.

Let x be the common multiple.

Quantity of Khoya = 7x 

Quantity of sugar = 2x

Total quantity of burfi = 18kg

$\Rightarrow \therefore \text{Total quantity of burfi = Quantity of Khoya+Quantity of sugar}$

$\Rightarrow 18=7x+2x$

$\Rightarrow 18=9x$

$\Rightarrow x=\dfrac{18}{9}=2$

\[\text{Quantity of Khoya} = 7x=7\times 2=14kg\]

51. A line segment 56cm long is to be divided into two parts in the ratio of 2: 5. Find the length of each part. 

Ans: The line segment is divided in the ratio = 2: 5

Let x be the common multiple.

So, the two parts will be 2x and 5x.

Total length of the line segment = Sum of the two parts

$ \Rightarrow 56 = 2x + 5x$

$ \Rightarrow 56 = 7x$

$ \Rightarrow x = \dfrac{{56}}{7} = 8$

\[\text{Length of part 1 of line segment}=2x=2\times 8=16cm\]

\[\text{Length of part 2 of line segment}=5x=5\times 8=40cm\]

\[\therefore \] Length of each part is 16cm and 40 cm.

52. The number of milk teeth in human beings is 20 and the number of permanent teeth is 32. Find the ratio of the number of milk teeth to the number of permanent teeth. 

Ans: No. of milk teeth in humans = 20

No. of permanent teeth in humans = 32

\[\Rightarrow Ratio=\dfrac{\text{No. of milk teeth in humans}}{\text{No. of permanent teeth in humans}}=\dfrac{20}{32}=\dfrac{5}{8}\]

Therefore, the ratio of the number of milk teeth to the number of permanent teeth is 5:8.

53. The sex ratio is defined as the number of females per 1000 males in the population. Find the sex ratio if there are 3732 females per 4000 males in a town. 

Ans: Given:

No. of females = 3732

No. of males = 4000

Let the No. of females per 1000 males be x.

$\dfrac{{3732}}{{4000}} = \dfrac{x}{{1000}}$

$ \Rightarrow x \times 4000 = 3732 \times 1000$

\[ \Rightarrow x = \dfrac{{3732 \times 1000}}{{4000}} = 933\]

$\therefore $ No. of females per 1000 males is 933.

$\therefore \text{Sex ratio = }\dfrac{933}{1000}$

54. In a year, Ravi earns Rs 360000 and paid Rs 24000 as income tax. Find the ratio of his 

(a) income to income tax. 

Ans:  Given:

Ravi’s annual income = Rs. 360000

Income tax paid by Ravi = Rs. 24000

$\Rightarrow Ratio=\dfrac{\text{Ravi’s annual income}}{\text{Income tax paid by Ravi}}=\dfrac{Rs.\,360000}{Rs.\,\text{24}000}=\dfrac{15}{1}$

Therefore, the ratio of Ravi’s income to the income tax paid by him is 15: 1.

(b) Income tax to income after paying income tax. 

Ans: Given:

Income tax paid by Ravi = Rs. 24000

\[\text{Income after paying income tax}=\text{Annual income - Income tax paid}\]

$=Rs.\,\text{3,60,000-Rs}\text{.}\,\text{24,000=Rs}\text{.}\,\text{3,36,000}$

$\Rightarrow Ratio=\dfrac{\text{Income tax paid by Ravi}}{\text{Income after paying tax}}=\dfrac{Rs.\,\text{24}000}{Rs.\,\text{336}000}=\dfrac{1}{14}$

Therefore, the ratio of income tax paid by Ravi to the income after paying tax is 1: 14.

55. Ramesh earns Rs 28000 per month. His wife Rama earns Rs 36000 per month. Find the ratio of 

(a) Ramesh’s earnings to their total earnings 

Ans: Ramesh’s earnings = Rs. 28000

Rama’s earnings = Rs. 36000

Total earnings = Rs. 28000 + Rs. 36000 = Rs. 64000

Ratio of Ramesh’s earnings to their total earnings

$\Rightarrow \dfrac{\text{Ramesh's earnings}}{\text{Total earnings }}=\dfrac{Rs.28000}{Rs.\text{64000}}=\dfrac{7}{16}$

Ratio of Ramesh’s earnings to their total earnings is 7: 16.

(b) Rama’s earnings to their total earnings.

Ans: Ratio of Rama’s earnings to their total earnings

$\Rightarrow \dfrac{\text{Rama's earnings}}{\text{Total earnings }}=\dfrac{Rs.\text{36}000}{Rs.\text{64000}}=\dfrac{9}{16}$

Ratio of Rama’s earnings to their total earnings is 9: 16.

56. Of the 288 persons working in a company, 112 are men and the remaining are women. Find the ratio of the number of 

(a) Men to that of women. 

Ans: Given:

Total no. of persons in the company = 288

Total no. of men in the company = 112

Total no. of women in the company = 288 – 112 = 176

Ratio of Men to that of women.

$\Rightarrow Ratio=\dfrac{\text{Total men}}{\text{Total women}}=\dfrac{112}{176}=\dfrac{7}{16}$

Ratio of Men to that of women is 7: 16.

(b) Men to the total number of persons. 

Ans: (b) Ratio of Men to the total number of persons.

$\Rightarrow Ratio=\dfrac{\text{Total men}}{\text{Total no. of persons}}=\dfrac{112}{288}=\dfrac{7}{18}$

Ratio of Men to the total number of persons.

(c) Women to the total number of persons. 

Ans: Ratio of Women to the total number of persons 7: 18.

$\Rightarrow Ratio=\dfrac{\text{Total  women}}{\text{Total no. of persons}}=\dfrac{176}{288}=\dfrac{11}{18}$

Ratio of Women to the total number of persons is 11: 18.

57. A rectangular sheet of paper is of length 1.2m and width 21cm. Find the ratio of the width of the paper to its length. 

Ans: Given:

Length = 1.2m = $1.2 \times 100 = 120cm$

Width = 21 cm

$ \Rightarrow Ratio = \dfrac{\text{width}}{\text{length}} = \dfrac{{21}}{{120}} = \dfrac{7}{{40}}$

Therefore, the ratio of the width of the paper to its length is 7: 40.

58. A scooter travels 120km in 3 hours and a train travels 120km in 2 hours. Find the ratio of their speeds.

Ans: Distance travelled by Scooter = 120km

Time taken by scooter = 3 hours

$\text{Speed of scooter} = \dfrac{\text{Distance travelled}}{\text{Time taken}}=\dfrac{120km}{3\text{hours}}=40km/hour$

Distance travelled by train = 120km

Time taken by train = 2 hours

$\text{Speed of train}=\dfrac{\text{Distance travelled}}{\text{Time taken}}=\dfrac{120km}{2\text{hours}}=60km/hour$

Now,

$\Rightarrow \text{Ratio}=\dfrac{\text{Speed of scooter}}{\text{Speed of train}}=\dfrac{40}{60}=\dfrac{2}{3}$

Ratio of speed of scooter to speed of train = 2:3.

59. An office opens at 9 a.m. and closes at 5.30 p.m. with a lunch break of 30 minutes. What is the ratio of lunch break to the total period in the office?

Ans: Given:

Office opens at 9 am.

Office closes at 5:30 pm.

Office Duration = 8 hours 30 min = ($8\times 60+30$) min = (480 + 30) min = 510 min

Duration of lunch break = 30 min

$\Rightarrow \text{Ratio}=\dfrac{\text{Duration of lunch break}}{\text{Total Office duration}}=\dfrac{30}{510}=\dfrac{1}{17}$

Therefore, the ratio of lunch break to the total period in the office is 1: 17.

60. The shadow of a 3m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24m long, how tall is the flagstaff? 

Ans: If the length of the stick is 3m, the height of the shadow is 4m.

So, if the length of the flagstaff is x m then the height of the shadow will be 24m.

$ \Rightarrow \dfrac{3}{4} = \dfrac{x}{{24}}$

$ \Rightarrow x = \dfrac{{24 \times 3}}{4} = 6 \times 3 = 18m$

Therefore, the length of the flagstaff is 18m.

61. A recipe calls for 1 cup of milk for every ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people? 

Ans: Total amount of cake mix for 6 persons = ($1 + 2\dfrac{1}{2}$) = ( $1 + \dfrac{5}{2}$ ) = $\dfrac{7}{2}$

$\therefore $ Total amount of cake mix for 8 persons will be x

\[ \Rightarrow \dfrac{{\dfrac{7}{2}}}{6} = \dfrac{x}{8}\]

$ \Rightarrow \dfrac{7}{{2 \times 6}} = \dfrac{x}{8}$

$ \Rightarrow \dfrac{7}{{12}} = \dfrac{x}{8}$

$ \Rightarrow x \times 12 = 7 \times 8$

$ \Rightarrow x = \dfrac{{7 \times 8}}{{12}} = \dfrac{{14}}{3}$

$\dfrac{{14}}{3}$ cups of both flour and milk will be needed to make a cake for 8 people.

62. In a school, the ratio of the number of large classrooms to small classrooms is 3:4. If the number of small rooms is 20, then find the number of large rooms. 

Ans: Ratio of no. of large classrooms to no. of small classrooms = 3: 4.

No. of small classrooms = 20.

Let the no. of large classrooms be x

$\Rightarrow \text{Ratio}=\dfrac{\text{No. of large classrooms}}{\text{No. of small classrooms}}$

$ \Rightarrow \dfrac{3}{4} = \dfrac{x}{{20}}$

$ \Rightarrow x = \dfrac{{3 \times 20}}{4} = 3 \times 5 = 15$

Therefore, No. of large classrooms = 15.

63. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of (a) The number of English newspapers to the number of Hindi newspapers. (b) The number of Hindi newspapers to the total number of newspapers. 

Ans: Total no. of newspapers = 312

No. of English newspapers = 216

No. of Hindi newspapers = Total no. of newspapers - No. of English newspapers

= 312 – 216 = 96

No. of Hindi newspapers = 96

(a) Ratio of the number of English newspapers to the number of Hindi newspaper =$ \dfrac{{216}}{{96}} = \dfrac{9}{4}$

Ratio of the number of English newspapers to the number of Hindi newspapers is 9: 4.

(b) Ratio of the number of Hindi newspapers to the total number of newspapers = 

$ \Rightarrow \dfrac{{96}}{{312}} = \dfrac{4}{{13}}$

Ratio of the number of Hindi newspapers to the total number of newspapers is 4: 13.

64. The students of a school belong to different religious backgrounds. The number of Hindu students is 288, the number of Muslim students is 252, the number of Sikh students is 144 and the number of Christian students is 72. Find the ratio of (a) The number of Hindu students to the number of Christian students. (b) The number of Muslim students to the total number of students 

Ans: No. of Hindu students = 288 

No. of Muslim students = 252 

No. of Sikh students = 144 

No. of Christian students = 72 

$\therefore $ Total no. of the students in school = (288 + 252 + 144 +72) = 756 

(a) Ratio of the no. of Hindu students to the no. of Christian students = $\dfrac{{288}}{{72}} = \dfrac{4}{1} = 4:1$

(b) Ratio of the no. of Muslim students to the total no. of students = $\dfrac{{252}}{{756}} = \dfrac{1}{3} = 1:3$

65. When Chinmay visited chowpati at Mumbai on a holiday, he observed that the ratio of North Indian food stalls to South Indian food stalls is 5:4. If the total number of food stalls is 117, find the number of each type of food stalls. 

Ans: Total number of food stalls = 117

Ratio of North Indian food stalls to South Indian food stalls = 5:4

Let x be the common multiple.

$\therefore $ No. of North Indian food stalls = 5x 

No. of South Indian food stalls = 4x

Now, 

Total no. of food stalls = No. of North Indian food stalls + No. of South Indian food stalls

$ \Rightarrow 117 = 5x + 4x$

$ \Rightarrow 117 = 9x$

$ \Rightarrow x = \dfrac{{117}}{9} = 13$

No. of North Indian food stalls \[=5x=5\times 13=65\]

No. of North Indian food stalls \[=\text{4x}=4\times 13=52\]

66. At the parking stand of Ramleela ground, Kartik counted that there are 115 cycles, 75 scooters, and 45 bikes. Find the ratio of the number of cycles to the total number of vehicles. 

Ans: Total no. of cycles = 115 

Total no. of scooter = 75

Total no. of bikes = 45 

$\therefore $ Total no. of vehicles = (115 + 75 +45) = 235 

\[Ratio=\dfrac{\text{No.of cycles}}{\text{No. of vehicles}}=\dfrac{115}{235}=\dfrac{23}{47}\]

Therefore, the ratio of the number of cycles to the total number of vehicles is 23: 47.

67. A train takes 2 hours to travel from Ajmer to Jaipur, which are 130km apart. How much time will it take to travel from Delhi to Bhopal which are 780km apart if the train is travelling at the uniform speed? 

Ans: The train is travelling at a uniform speed.

The train covers 130km in 2 hours.

So, the train will cover 780km in x hours.

$ \Rightarrow Ratio = \dfrac{{130km}}{{780km}} = \dfrac{{2 hours}}{x}$

$ \Rightarrow x = \dfrac{{780 \times 2}}{{130}} = 12hours$

The train will take 12 hours to travel from Delhi to Bhopal which are 780km apart.

68. The length and breadth of a school ground are 150m and 90m respectively, while the length and breadth of a Mela ground are 210m and 126m, respectively. Are these measurements in proportion? 

Ans: Length of school ground = 150m

Breadth of school ground = 90m

$ \Rightarrow Ratio = \dfrac{{150}}{{90}} = \dfrac{5}{3}$

The ratio of the length of school garden to breadth of school garden = 5:3.

Similarly,

Length of Mela ground = 210m

Breadth of Mela ground = 126m

$ \Rightarrow Ratio = \dfrac{{210}}{{126}} = \dfrac{5}{3}$

The ratio of the length of Mela garden to the breadth of Mela garden = 5:3.

Both the ratios are equal.

Hence, the ratios are in proportion.

69. In Fig. 8.4, the comparative areas of the continents are given: What is the ratio of the areas of 

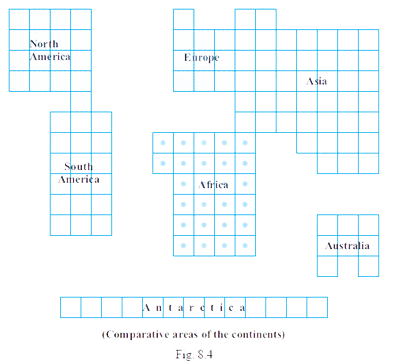
(a) Africa to Europe 

Ans: Each square = 1 unit

(a) Area of Africa = 26 unit2

Area of Europe = 10 unit2

$Ratio=\dfrac{\text{Area of Africa}}{\text{Area of Europe}}=\dfrac{26}{10}=\dfrac{13}{5}$

The ratio of the areas of Africa to Europe is 13: 5.

(b) Australia to Asia 

Ans: Area of Australia = 8 unit2

Area of Asia = 44 unit2

$\text{Ratio}=\dfrac{\text{Area of Australia}}{\text{Area of Asia}}=\dfrac{8}{44}=\dfrac{2}{11}$

The ratio of the areas of Australia to Asia is 2: 11.

(c) Antarctica to the Combined area of North America and South America.

Ans: Area of Antarctica = 8 unit2

Area of Combined area of North America and South America = 44 unit2

$\text{Ratio}=\dfrac{\text{Area of Antarctica}}{\text{Area of Combined area of (North America+South America)}}=\dfrac{13}{(17+18)}=\dfrac{13}{35}$

The ratio of the areas of Antarctica to Combined area of North America and South America is 13: 35.

70. A tea merchant blends two varieties of tea costing her Rs 234 and Rs 130 per kg in the ratio of their costs. If the weight of the mixture is 84kg, then find the weight of each variety of tea.

Ans: Ratio of the costs of two varieties of tea =\[\dfrac{Rs.234}{Rs.\text{130}}=\dfrac{9}{5}\]

Let x be the common multiple.

Therefore, total weight = 9x + 5x = 14x

$\Rightarrow \therefore 84=14x$

$\Rightarrow x=\dfrac{84}{14}=6$

Thus, Weight of tea with price Rs. 234 \[=9x=9\times 6=54kg\] 

Weight of tea with price Rs. 130 \[=5x=5\times 6=30kg\]

71. An alloy contains only zinc and copper and they are in the ratio of 7:9. If the weight of the alloy is 8kg, then find the weight of copper in the alloy. 

Ans: Total weight of the alloy = 8kg.

Ratio of Zinc and copper = $\dfrac{7}{9}$

Let x be the common multiple.

Thus, the weight of zinc = 7x and the weight of copper = 9x.

Total weight of alloy = weight of zinc + weight of copper

$ \Rightarrow 8kg = 7x + 9x$

$ \Rightarrow 8kg = 16x$

$ \Rightarrow x = \dfrac{8}{{16}} = \dfrac{1}{2}$

Weight of copper = 9x = $9 \times \dfrac{1}{2} = 4\dfrac{1}{2} = 4.5kg$

72. In the following figure 8.4, each division represents 1cm: Express numerically the ratios of the following distances: 

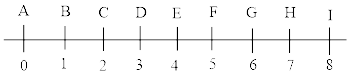
(i) AC: AF 

Ans: Ratios of AC: AF = $\dfrac{{AC}}{{AF}} = \dfrac{{2cm}}{{5cm}} = \dfrac{2}{5} = 2:5$

(ii) AG: AD 

Ans: Ratios of AG: AD = $\dfrac{{AG}}{{AD}} = \dfrac{{6cm}}{{3cm}} = \dfrac{2}{1} = 2:1$

(iii) BF: AI 

Ans: Ratios of BF: AI = $\dfrac{{BF}}{{AI}} = \dfrac{{4cm}}{{8cm}} = \dfrac{1}{2} = 1:2$

(iv) CE: DI 

Ans: Ratios of CE: DI = $\dfrac{{CE}}{{DI}} = \dfrac{{2cm}}{{5cm}} = \dfrac{2}{5} = 2:5$

73. Find two numbers whose sum is 100 and whose ratio is 9:16. 

Ans: Ratio of the two numbers = $\dfrac{9}{{16}}$

Let x be the common multiples. So, the two numbers will be 9x and 16x.

Sum of two numbers = 9x + 16x

$ \Rightarrow 100 = 25x$

$ \Rightarrow x = \dfrac{{100}}{{25}} = 4$

The two numbers are:

9x = $9 \times 4 = 36$ and 16x = $16 \times 4 = 64$

74. In Fig. 8.6 (i) and Fig. 8.6 (ii), find the ratio of the area of the shaded portion to that of the whole figure:

(i).

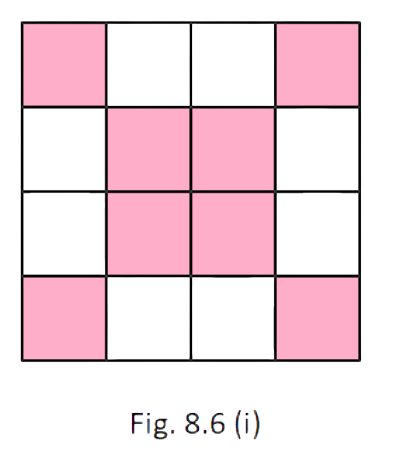
Ans: Area of shaded portion = 8 unit2

Area of whole figure = 16 unit2

\[\text{Required Ratio}=\dfrac{\text{Area of shaded portion}}{\text{Area of whole figure}}=\dfrac{8uni{{t}^{2}}}{\text{16}uni{{t}^{2}}}=\dfrac{1}{2}\]

Ratio of the area of the shaded portion to that of the whole figure = 1:2.

(ii).

Ans: Area of shaded portion = 16 unit2

Area of whole figure = 32 unit2

\[\operatorname{Re}quired Ratio=\dfrac{\text{Area of shaded portion}}{\text{Area of whole figure}}=\dfrac{\text{16} uni{{t}^{2}}}{\text{32} uni{{t}^{2}}}=\dfrac{1}{2}\]

Ratio of the area of the shaded portion to that of the whole figure = 1:2.

75. A typist has to type a manuscript of 40 pages. She has typed 30 pages of the manuscript. What is the ratio of the number of pages typed to the number of pages left? 

Ans: Total no. of pages in manuscript = 40 

No. of pages typed in manuscript = 30 

No. of pages left = 40 – 30 = 10 

$ \Rightarrow Ratio = \dfrac{{30}}{{10}} = \dfrac{3}{1}$

Ratio of the number of pages typed to the number of pages left = 3:1

76. In a floral design made from tiles each of dimensions 40cm by 60cm (See Fig. 8.7), find the ratios of: 

(a) The perimeter of the shaded portion to the perimeter of the whole design. 

Ans: Measurements of tile:

Length = 60cm

Breadth = 40cm

Perimeter of shaded portion = $(4\times 60+6\times 40)cm=480cm$

Perimeter of whole portion = $(8\times 60+10\times 40)cm=880cm$

$\Rightarrow Ratio=\dfrac{\text{Perimeter of shaded portion}}{\text{Perimeter of whole portion}}=\dfrac{480cm}{880cm}=\dfrac{6}{11}$

The perimeter of the shaded portion to the perimeter of the whole design is 6:11.

(b) The area of the shaded portion to the area of the unshaded portion. 

Let’s calculate area of one tile = $l\times b=60cm\times 40cm=2400c{{m}^{2}}$

 $\text{Area of shaded portion}$ = $6\times \text{Area of one tile} = 6 \times 2400c{{m}^{2}}=14400c{{m}^{2}}$

$\text{Area of unshaded portion}$ = $14\times \text{Area of one tile} =14\times 2400c{{m}^{2}}=33600c{{m}^{2}}$

$\Rightarrow Ratio=\dfrac{\text{Area of shaded portion}}{\text{Area of unshaded portion}}=\dfrac{14400cm}{33600cm}=\dfrac{3}{7}$

The area of the shaded portion to the area of the unshaded portion is 3:7.

77. In Fig. 8.8, what is the ratio of the areas of 

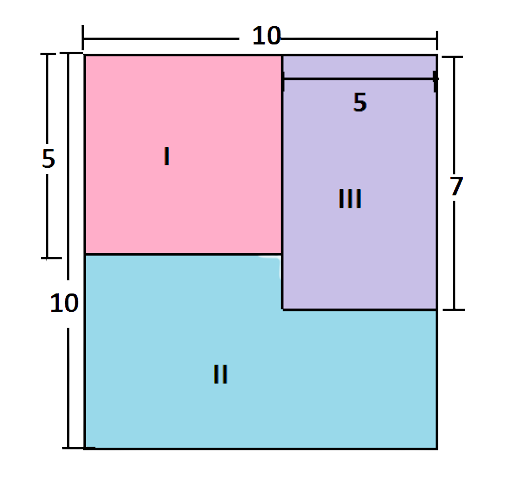
(a) Shaded portion I to shaded portion II?

Ans: Part I is a square,

Area of the shaded Part I = $side\times side=5unit\times 5unit=25uni{{t}^{2}}$

Part III is a rectangle,

Area of the shaded Part III = $l\times b=5unit\times 7unit=35uni{{t}^{2}}$

Area of the shaded Part II = $\left[\left( 10\text{unit}\times 10\text{unit} \right)-25uni{{t}^{2}}-35uni{{t}^{2}} \right]=\left( 100uni{{t}^{2}}-60uni{{t}^{2}} \right)=40uni{{t}^{2}}$

$Ratio=\dfrac{\text{Shaded portion I}}{\text{Shaded portion II}}=\dfrac{25 uni{{t}^{2}}}{40 uni{{t}^{2}}}=\dfrac{5}{8}$

The ratio of Shaded portion I to shaded portion II is 5:8.

(b) Shaded portion II to shaded portion III?

Ans: \[ Ratio=\dfrac{\text{Shaded portion II}}{\text{Shaded portion III}}=\dfrac{40 uni{{t}^{2}}}{35 uni{{t}^{2}}}=\dfrac{8}{7}\]

The ratio of Shaded portion II to shaded portion III is 8:7.

(c) Shaded portions I and II taken together and shaded portion III?

Ans: \[ Ratio=\dfrac{\text{Shaded portion I and II taken together}}{\text{Shaded portion III}}=\dfrac{(25+40) uni{{t}^{2}}}{35 uni{{t}^{2}}}=\dfrac{65 uni{{t}^{2}}}{35 uni{{t}^{2}}}=\dfrac{13}{7}\]

The ratio of Shaded portion I and II taken together to shaded portion III is 13:7.

78. A car can travel 240km in 15 litres of petrol. How much distance will it travel in 25 litres of petrol? 

Ans: A car can travel 240km in 15 litres of petrol.

So, a car can travel x km in 25 litres of petrol

$ \Rightarrow \dfrac{{15}}{{240}} = \dfrac{{25}}{x}$

$ \Rightarrow 15 \times x = 25 \times 240$

$ \Rightarrow x = \dfrac{{25 \times 240}}{{15}} = 400km$

The car can travel 400 km in 25 litres of petrol.

79. Bachhu Manjhi earns Rs 24000 in 8 months. At this rate, 

(a) How much does he earn in one year? 

Ans: One year has 12 months.

Bachhu Manjhi earns Rs 24000 in 8 months. So, he will earn x Rs. in 1 year (12 months).

$\Rightarrow Ratio=\dfrac{Rs.\text{24000}}{8}=\dfrac{Rs.\text{x}}{12}$

$\Rightarrow x=\dfrac{Rs.\text{24000}\times 12}{8}=\dfrac{Rs.\text{288000}}{8}=Rs.\text{36000}$

Therefore, he will earn Rs. 36000 in one year.

(b) In how many months does he earn Rs 42000? 

Ans: Bachhu Manjhi earns Rs 24000 in 8 months. So, he will earn Rs. 42000 in y months.

$\Rightarrow Ratio=\dfrac{Rs.\text{24000}}{8}=\dfrac{Rs.\text{42000}}{y}$

$\Rightarrow y=\dfrac{Rs.\text{42000}\times 8}{Rs.24000}=\dfrac{Rs.\text{336000}}{Rs.24000}=14 \text{ months}$

$\Rightarrow 14\text{months = 1year 2 months}$

Hence, he will earn Rs. 42000 in 1 year 2 months.

80. The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals? 

Ans: The yield of wheat from 8 hectares of land is 360 quintals.

So, the number of hectares of land required for a yield of 540 quintals be x.

\[\Rightarrow Ratio=\dfrac{360\text{ quintals}}{8\text{ hectares}}=\dfrac{540\text{ quintals}}{x\text{ hectares}}\]

$ \Rightarrow x = \dfrac{{540 \times 8}}{{360}} = \dfrac{{4320}}{{360}} = 12$

Therefore, the number of hectares of land required for a yield of 540 quintals is 12 hectares.

81. The Earth rotates 360o about its axis in about 24 hours. By how much degree will it rotate in 2 hours? 

Ans: The Earth rotates 360o in 24 hours. So, let the rotation in 2 hours be xo

\[ \Rightarrow Ratio = \dfrac{{{{360}^o}}}{{{x^o}}} = \dfrac{{24}}{2}\]

$ \Rightarrow x = \dfrac{{{{360}^o} \times 2}}{{24}} = \dfrac{{720}}{{24}} = {30^o}$

Therefore, the earth’s rotation in 2 hours is 30o.

82. Shivangi is suffering from anemia as the haemoglobin level in her blood is lower than the normal range. Doctor advised her to take one iron tablet two times a day. If the cost of 10 tablets is Rs 17, then what amount will she be required to pay for her medical bill for 15 days? 

Ans: Shivangi will consume 2 tablets daily. 

So, in 15 days she will consume = $2 \times 15 = 30{\text{ }}tablets$

Set of 10 tablets cost Rs. 17.

Let the cost of 30 tablets be x.

$\Rightarrow Ratio=\dfrac{10\text{ Tablets}}{17\text{Rs}\text{.}}=\dfrac{30\text{ Tablets}}{x\text{ Rs}\text{.}}$

$\Rightarrow x=\dfrac{30\times 17}{10}=Rs.\text{51}$

She will pay Rs. 51 for a medical bill of 15 days.

83. The quarterly school fee in Kendriya Vidyalaya for Class VI is Rs 540. What will be the fee for seven months? 

Ans: 1 quarterly is 3 months.

Quarterly fee is 540 Rs.

So, let the fee for 7 months be x.

$\Rightarrow Ratio=\dfrac{\text{3months}}{\text{Rs}\text{.540}}=\dfrac{\text{7months}}{x\text{Rs}\text{.}}$

$\Rightarrow x=\dfrac{Rs.\text{54}0\times 7}{3}=Rs.\text{1260}$

School fee for 7 months is Rs. 1260.

84. In an election, the votes cast for two of the candidates were in the ratio 5: 7. If the successful candidate received 20734 votes, how many votes did his opponent receive?

Ans: Ratio of votes cast for the candidates = 5:7.

Let the common multiple be x.

The winning candidate received 7x votes and the opposing (losing) candidate received 5x.

Total votes of the winning candidate = 20734.

Let the votes for the opponent candidate be x.

$\Rightarrow Ratio=\dfrac{5}{7}=\dfrac{\text{x} \text{ votes}}{20734 \text{ votes}}$

$\Rightarrow x=\dfrac{5\times 20734\text{ votes}}{7}=2962$

$\therefore $ Votes received by the opponent candidate = 5x = $5\times 2962=14810\text{ }votes$

85. A metal pipe 3 meter long was found to weigh 7.6kg. What would be the weight of the same kind of 7.8m long pipe? 

Ans: Weight of a 3 metre pipe = 7.6 kg

Let the weight of the 7.8 metre pipe be x.

$ \Rightarrow Ratio = \dfrac{{3m}}{{7.8m}} = \dfrac{{7.6kg}}{{xkg}}$

$ \Rightarrow x = \dfrac{{7.6kg \times 7.8m}}{{3m}} = 19.76kg$

Therefore, the weight of the 7.8m long pipe is 19.76 kg.

86. A recipe for raspberry jelly calls for 5 cups of raspberry juice and $2\dfrac{1}{2}$ cups of sugar. Find the amount of sugar needed for 6 cups of the juice? 

Ans: For the recipe,

5 cups of raspberry juice need $2\dfrac{1}{2}$ cups of sugar.

So, 6 cups of raspberry juice will need x cups of sugar.

$\Rightarrow Ratio=\dfrac{\text{5 cups of raspberry juice}}{\dfrac{5}{2}\text{cups of sugar}}=\dfrac{\text{6 cups of raspberry juice}}{\text{x cups of sugar}}$

$\Rightarrow x=\dfrac{6\times \dfrac{5}{2}}{5}=\dfrac{15}{5}=3$

Therefore, the amount of sugar needed for 6 cups of the juice is 3.

87. A farmer planted 1890 tomato plants in a field in rows each having 63 plants. A certain type of worm destroyed 18 plants in each row. How many plants did the worm destroy in the whole field?

Ans: Total no. tomato plants = 1890 and

No. of tomato plants in each row = 63.

$\therefore \text{No. of rows=}\dfrac{\text{Total no. of tomato plants}}{\text{No. of tomato plants in each row}}=\dfrac{1890}{63}=30\text{ rows}$

Plants destroyed in each row = 18 plants

So, the total no. of plants destroyed by the worm = No. of rows $\times $ Plants destroyed in each row

$\Rightarrow 30\times 18=540\text{ plants}$

The worm destroyed a total of 540 plants in the whole field.

88. Length and breadth of the floor of a room are 5m and 3m, respectively. Forty tiles, each with area $\dfrac{1}{16}{{m}^{2}}$ , were used to cover the floor partially. Find the ratio of the tiled and the non-tiled portion of the floor.

Ans: Length of the floor = 5m

Breadth of the floor = 3m

$\therefore $ Area of the floor = \[\text{Length}\times \text{breadth}=5m\times 3m=15{{m}^{2}}\]

Area of 1 tile = $\dfrac{1}{16}{{m}^{2}}$

$\therefore $ Area of tiled floor = $40\times \dfrac{1}{16}{{m}^{2}}=\dfrac{5}{2}{{m}^{2}}$

Area of non-tiled floor = Total area – area of tiled floor = \[15{{m}^{2}}-\dfrac{5}{2}{{m}^{2}}=\dfrac{25}{2}{{m}^{2}}\]

$\Rightarrow Ratio=\dfrac{\text{Tiled area}}{\text{Non-tiled area}}=\dfrac{\dfrac{5}{2}}{\dfrac{25}{2}}=\dfrac{5}{25}=\dfrac{1}{5}$

The ratio of the tiled portion to the non-tiled portion of the floor is 1:5.

89. A carpenter had a board which measured 3m × 2m. She cut out a rectangular piece of 250cm × 90cm. What is the ratio of the area of the cut out piece and the remaining piece?

Ans: Given:

Length of the board = 3m = 300cm

Breadth of the board = 2m = 200cm

Area of the board = $(300cm\times 200cm)=60000c{{m}^{2}}$

Length of the rectangular piece cut = 250cm

Breadth of the rectangular piece cut = 90cm

Area of the rectangular piece cut = $(250cm\times 90cm)=22500c{{m}^{2}}$

Thus,

Area of remaining piece = Area of the board - Area of the rectangular piece cut

$\Rightarrow 60000c{{m}^{2}}-22500c{{m}^{2}}=37500c{{m}^{2}}$

$\Rightarrow Ratio=\dfrac{\text{Area of the cut out piece}}{\text{Area of remaining piece}}=\dfrac{22500c{{m}^{2}}}{37500c{{m}^{2}}}=\dfrac{3}{5}$

The ratio of the area of the cut out piece and the remaining piece is 3:5.

Importance of Class 6 Maths Syllabus

Class 6 Math lays the foundation for future math classes. Having solid concepts will aid in the achievement of high grades. Instead of memorizing the method of answering the questions, you should concentrate on comprehending the issues at hand. By using a variety of practice papers, you will understand the many sorts of questions that might be posed in the test. It also provides you with an understanding of exam patterns, marking schemes, and the types of questions asked in the exam.

Class 6 Maths Syllabus

About Chapter 8

Chapter 8 of Class 6 Maths is all about ratio and proportion. They can be explained majorly based on fractions. The ratio is a term used to compare two or more numbers. Proportion is used to indicate how big or small a quantity is when compared to the other. It is denoted in the form of a:b. To know more about the chapter, download the solutions from Vedantu.

Last-minute tips for acing Class 6 Maths Exam

Here are some tips and tricks students can consider during their preparation of the subject in Class 6:

• When you obtain your question paper, you first need to figure out how long each question will take. You must plan your time based on your preferences. Remember that if you spend too much time on one question, you may lose points elsewhere as you miss out on the chance to attempt it.

• You must utilize your reading time to plan responses to the paper's most tough and high-mark questions. In the best-case situation, you'll be able to construct a solution and make note of it quickly.

• While not required by the question, making a diagram has several advantages. You will be able to see the key characteristics of the question and the missing piece. Instead of remembering everything, you will have everything on paper.

•  It is critical to start with the basics, such as defining the unknowns, creating a picture, formulating, or recognizing the problem. Then you must write the answer step-by-step. It will help you structure your answer and show your teacher your thought process.

• You must respond in the format asked. After you have solved the issue and recorded your response, reread the question to ensure you have answered it correctly. Highlight the question portion that tells you how to write your answer, so you don't miss it.

To learn more about ratio and proportion, download the NCERT Exemplar file from Vedantu and start solving the questions. Get assistance from the solution provided by the top experts to understand how the concepts have been used. Define your preparation for the chapter and proceed to make a stronger conceptual foundation to score more in the exams.