NCERT Exemplar for Class 11 Physics - Thermal Properties of Matter - Free PDF Download
FAQs on NCERT Exemplar for Class 11 Physics Chapter 11 - Thermal Properties of Matter (Book Solutions)
1. What does the Thermal property of Matters signify?
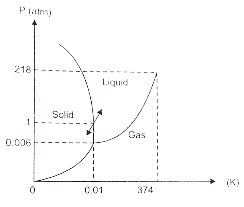
A Physical Matter can have a number of properties that determine its state and behaviorism. The Thermal property of a particular Matter signifies the state and characteristics of the particular Matter under a particular temperature range. When heat is conducted through a particular Matter, the behaviorism and the properties of that particular Matter that we can perceive are known as Thermal properties. There are various components of Thermal properties that can be further explained by the laws of Physics.
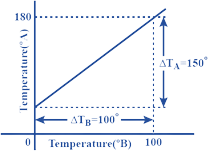
2. What is the relationship between the Thermal properties and the temperature of a particular Matter?
A Physical Matter can be present in various types of states. The form of state in which a particular Matter exists is further determined by the positions of various particles that it is constituted of and by the physical properties of the Matter. The Matter can show distinguishable characteristics if we can alter the temperature ranges. There are various physical laws that can explain the change of behaviorism of Matter when it is placed under different temperature ranges or when heat passes through the particles of Matter.
3. How many types of Thermal properties are there?
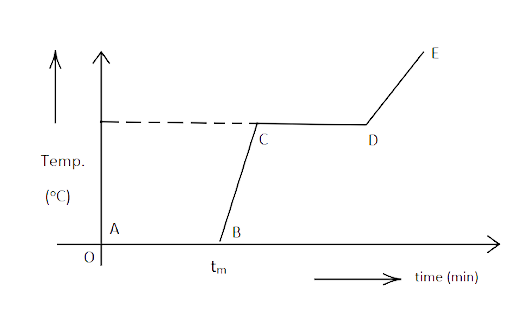
The various types of Thermal properties explain the reasons for the different kinds of behaviorism and characteristics displayed by a particular Matter when heat passes through them. For Example, heat capacity defines one of the physical properties of Matter. It refers to the amount of heat that is needed to pass through the particles of a Matter in order to produce a specific amount of change in the temperature. Another physical property of a Matter is known as Thermal Expansion and it denotes the change of the physical and outward properties of the Matter like the shape, volume, density, etc. Thermal conductivity explains the amount of energy produced in a particular Matter due to the movement of the molecules and particles under a particular temperature range.
4. How many types of Thermal Expansion are there?
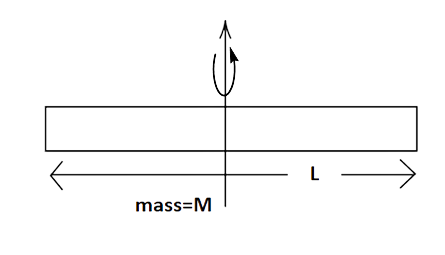
The term itself explains the significance of this particular physical property of Matters. If the Matter is placed under a definite range of temperature or a specific amount of heat is transmitted through the molecules and particles of the Matter, their outward properties will change and hence the characteristics of the Matter will also be altered. Three types of Thermal Expansion are known. Depending on the particular dimension of the Matters where the changes take place, there can be three types of Thermal Expansions and they are areal Expansion, linear and volumetric Expansion.
5. What is the significance of understanding the concept of Thermal properties of Matter?
The concept is introduced by CBSE to the students of Class 11 and the Thermal properties of Matter are considered one of those foundational concepts of Physics. It helps the students to understand and acquire a detailed knowledge of the various properties of Matters including the Thermal properties of a particular Matter. By understanding these concepts the students can explain the reasons why a particular Matter changes its characteristics when it is placed under different ranges of temperature or heat passes through it. The laws of Physics also explain what can be the characteristics displayed by the Matter under different temperature ranges. To know more you can visit the Vedantu website to get all the important course materials for even better preparation.