Question

Write the equation of tangent at (1,1) on the curve \[2{{x}^{2}}+3{{y}^{2}}=5\].

Answer 1

Hint: Here, we have been given the equation of a curve as \[2{{x}^{2}}+3{{y}^{2}}=5\] and we have to find the equation of its tangent at (1,1). For this, we will first give the general equation of of the tangent to any curve which is given as follows:
The tangent at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to any curve is given as:
$\left( y-{{y}_{1}} \right)={{\left( \dfrac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)$
Then we will find the value of $\dfrac{dy}{dx}$ by differentiating both sides of the equation of the curve with respect to x and then we will keep x=1 and y=1 in the then obtained value of $\dfrac{dy}{dx}$ to obtain the value of ${{\left( \dfrac{dy}{dx} \right)}_{\left( 1,1 \right)}}$. Then we will keep all these values in the general equation of the curve and hence we will obtain the required equation of the curve.

Complete step by step answer:
Here, we have been given the equation of the curve \[2{{x}^{2}}+3{{y}^{2}}=5\] and we have to find the equation of its tangent at the point (1,1).

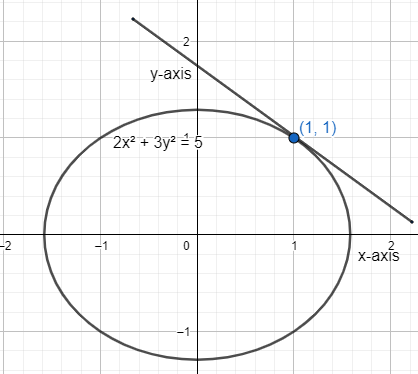
Now, we know that the tangent at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to any curve is given as:
$\left( y-{{y}_{1}} \right)={{\left( \dfrac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)$
So, we will first find the value of $\dfrac{dy}{dx}$ .
The equation of the curve given to us is:
\[2{{x}^{2}}+3{{y}^{2}}=5\]
Differentiating with respect to ‘x’ on both sides we get:
$\begin{align}
  & \dfrac{d}{dx}\left( 2{{x}^{2}}+3{{y}^{2}} \right)=\dfrac{d}{dx}\left( 5 \right) \\
 & \Rightarrow 2\left( 2x \right)+3\left( 2y \right).\dfrac{dy}{dx}=0 \\
 & \Rightarrow 4x+6y\dfrac{dy}{dx}=0 \\
\end{align}$
Hence, we get the value of $\dfrac{dy}{dx}$ as:
$\begin{align}
  & 4x+6y\dfrac{dy}{dx}=0 \\
 & \Rightarrow \dfrac{dy}{dx}=-\dfrac{4x}{6y} \\
 & \Rightarrow \dfrac{dy}{dx}=-\dfrac{2x}{3y} \\
\end{align}$
Hence, the value of $\dfrac{dy}{dx}$ is $-\dfrac{2x}{3y}$.
Now, w=here we have been given that $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,1 \right)$
Hence, we get the value of $\dfrac{dy}{dx}$ at (1,1) as:
$\begin{align}
  & \dfrac{dy}{dx}=-\dfrac{2x}{3y} \\
 & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{\left( 1,1 \right)}}=-\dfrac{2\left( 1 \right)}{3\left( 1 \right)} \\
 & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{\left( 1,1 \right)}}=-\dfrac{2}{3} \\
\end{align}$
Hence, the required value of $\dfrac{dy}{dx}$ is $-\dfrac{2}{3}$.
Now, putting these values in the general equation of the tangent we get:
$\left( y-1\right)={{\left( \dfrac{-2}{3} \right)}_{\left( 1,1 \right)}}\left( x-1 \right)$
3y-3=-2x+2
2x+3y=5

Hence, the required equation of the tangent to the given curve is 2x+3y=5.

Note: We here can find the equation of the tangent to the curve by using T=0. This method is used to find the equations of tangents to curves with degree 2. This is explained as follows:
If there is any variable in x or y with power 2, it is modified as follows (here, $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point on the curve on which we need to find the tangent):
$\begin{align}
  & {{x}^{2}}\to {{x}_{1}}x \\
 & {{y}^{2}}\to {{y}_{1}}y \\
\end{align}$
If there is any variable in x or y with power 1, it is modified as follows:
$\begin{align}
  & x\to \dfrac{1}{2}\left( x+{{x}_{1}} \right) \\
 & y\to \dfrac{1}{2}\left( y+{{y}_{1}} \right) \\
\end{align}$
If there is any constant in the equation of the curve, it remains the same.
Now, using T=0 in the given equation of the curve we get:
$\begin{align}
  & 2{{x}^{2}}+3{{y}^{2}}=5 \\
 & \Rightarrow 2\left( 1.x \right)+3\left( 1.y \right)=5 \\
 & \therefore 2x+3y=5 \\
\end{align}$