Question

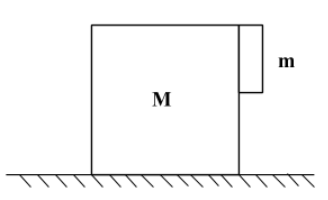
With what minimum acceleration, mass M must be moved on a frictionless surface so that m remains stuck to it as shown? The coefficient of friction between M and m is $\mu$.

A.$\dfrac {g} {\mu}$
B.$\mu g$
C.$2 \mu g$
D.$\dfrac {2g} {\mu}$

Answer 1

Hint: Friction force is the force which is produced by two surfaces when they come in contact with each other and slide against each other. The maximum resistive force applied by the body against the applied force to remain in its state of motion is called the coefficient of friction. To solve this problem, use the formula for force of friction or friction force. Then, use the newton’s law of motion. Equate these two equations and calculate the minimum acceleration for the mass M.

Complete answer:
The force of friction is given by,
$F = \mu N$ …(1)
Where, N is the normal force of m on the surface of M
             $\mu$ is the coefficient of friction
For mass m to stick to M while M is moving with acceleration, it has to move with the same acceleration with which M is moving.
Therefore, according to Newton’s second law of motion,
$F = mg$ …(2)
Equating equation. (1) and (2) we get,
$\mu N = ma$ …(3)
But, the normal force is given by,
$N= m.a$
Substituting this value in the equation. (3) we get,
$\mu \times m.a = mg$
$\Rightarrow \mu . a= g$
$\Rightarrow a= \dfrac {g}{\mu}$
Hence, the minimum acceleration should be $\dfrac {g}{\mu}$.

So, the correct answer is option A i.e. $\dfrac {g}{\mu}$.

Note:
Friction force can never be greater than the applied force. Whenever the frictional force is greater than the applied force, the friction force adjusts itself so that it becomes less as compared to the applied force. Friction force is dependent on the angle and the location of the object. The direction of force and friction force are always in opposite directions. Coefficient of friction is a dimensionless quantity.