Questions & Answers
Question
AnswersWhich of this is/are incorrect in the flow chart?
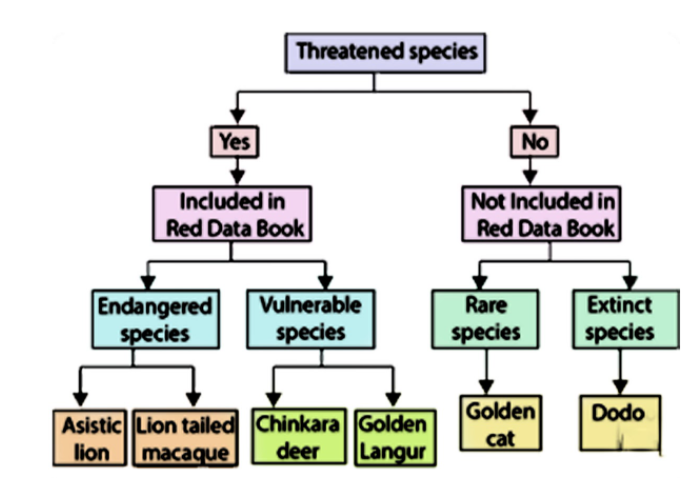
(A)Asiatic lion and lion-tailed macaque
(B)Vulnerable species
(C)Dodo
(D)Golden cat and chinkara deer
Answer
Verified92.7k+ views
Hint: It is a medium-sized cat with a head-to-body length of 66–105 cm (26–41 in), with a 40–57 cm (16–22 in) long tail, and is 56 cm (22 in) tall at the shoulder. It remains at 65 cm (26 in) tall and weighs around 23 kg (51 lb). And the other one has a reddish-buff summer coat with smooth, glossy fur. In winter, the white belly and throat fur are in greater contrast.
Complete answer:
Asian golden cat may be a medium-sized cat of Southeast Asia, which is assessed as vulnerable by IUCN and is listed in the Vietnam Red Data Book. In the IUCN Indian Red Data Book, the chinkara is put as vulnerable (1994), however from that point proposed in 1998 as lower hazard least concern (National) and information inadequate (Global).
Additional Information: The Asian golden cat is polymorphic in color. Golden, ruddy earthy colored, and buff-earthy colored people were recorded in northeastern India and Bhutan Reddish-earthy colored transforms were recorded in Sumatra. Melanistic individuals were recorded within the eastern Himalayas and in Sumatra. A spotted Asian golden cat with large rosettes on shoulders, flanks, and hips was described for the primary time as a specimen from China in 1872. This transform was recorded in China, Bhutan, and West Bengal's Buxa Tiger Reserve.
The chinkara, sides of the face have dim chestnut stripes from the edge of the thoughtfulness regarding the gag, circumscribed by white stripes. Its horns reach over 39 cm (15 in)
So the correct answer is ‘Golden cat and chinkara deer’
Note: Female Asian golden cats are sexually mature somewhere in the range of 18 and twenty-four months, while males develop at twenty-four years. Females inherit estrus every 39 days, at which era they leave markings and seek contact with the male by adopting receptive postures. During intercourse, the male will seize the skin of the neck of the feminine together with his teeth. After a gestation of 78 to 80 days, the feminine gives birth during a sheltered place to a litter of 1 to 3 kittens.
Complete answer:
Asian golden cat may be a medium-sized cat of Southeast Asia, which is assessed as vulnerable by IUCN and is listed in the Vietnam Red Data Book. In the IUCN Indian Red Data Book, the chinkara is put as vulnerable (1994), however from that point proposed in 1998 as lower hazard least concern (National) and information inadequate (Global).
Additional Information: The Asian golden cat is polymorphic in color. Golden, ruddy earthy colored, and buff-earthy colored people were recorded in northeastern India and Bhutan Reddish-earthy colored transforms were recorded in Sumatra. Melanistic individuals were recorded within the eastern Himalayas and in Sumatra. A spotted Asian golden cat with large rosettes on shoulders, flanks, and hips was described for the primary time as a specimen from China in 1872. This transform was recorded in China, Bhutan, and West Bengal's Buxa Tiger Reserve.
The chinkara, sides of the face have dim chestnut stripes from the edge of the thoughtfulness regarding the gag, circumscribed by white stripes. Its horns reach over 39 cm (15 in)
So the correct answer is ‘Golden cat and chinkara deer’
Note: Female Asian golden cats are sexually mature somewhere in the range of 18 and twenty-four months, while males develop at twenty-four years. Females inherit estrus every 39 days, at which era they leave markings and seek contact with the male by adopting receptive postures. During intercourse, the male will seize the skin of the neck of the feminine together with his teeth. After a gestation of 78 to 80 days, the feminine gives birth during a sheltered place to a litter of 1 to 3 kittens.