Question

Which of the following values is not a possible value of $ \sin x $ ?
(A) $ \dfrac{3}{4} $
(B) $ \dfrac{3}{5} $
(C) \[\dfrac{4}{5}\]
(D) $ \dfrac{5}{4} $

Answer 1

Hint: Draw the graph of $ \sin x $ and find the range of $ \sin x $ . From the range of $ \sin x $ , we can check which values in the option satisfy the range of $ \sin x $ and which do not. In simple terms, range is the collection of points on the Y-axis from which the graph exists.

Complete step-by-step answer:
Observe the graph

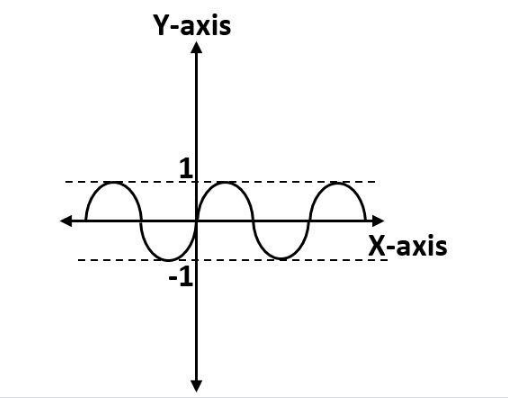
Given above is the rough sketch of the graph of $ \sin x $ .
From this graph, you can observe a very important thing. That is, the maximum value of $ \sin x $ is $ = 1 $ and the minimum value of $ \sin x = - 1 $
That means, $ \sin x $ can never be greater than one and $ \sin x $ can never be less than minus one.
Mathematically, we can write it as,
 $ - 1 \leqslant \sin x \leqslant 1 $ . . . (1)
Now clearly, the values in option (A), (B), (C) are less than one. i.e. they lie in the interval of equation (1) as in all three options, the numerator is less than the denominator. And we know that, if the numerator is less than the denominator then the value of the fraction is always less than one.
Therefore, options (A), (B), (C) are all incorrect.
But option (D) $ \dfrac{5}{4} = 1.25 > 1 $
Thus, $ \sin x $ cannot be equal to this value.
Thus, $ \dfrac{5}{4} $ is not the possible value of $ \sin x $
Therefore, from the above explanation, the correct answer is, option (D) $ \dfrac{5}{4} $
So, the correct answer is “Option D”.

Note: The key point in this question was knowing the range of $ \sin x $ . If you know the range of $ \sin x $ then you don’t even need to draw the graph to check it. And then the question becomes paperless, as you can directly say that option (D) is the correct answer, just by looking at the options. Therefore, graphs and properties related to graphs are important.