Question

Which of the following has trimerous symmetric flowers?
a. Cactus
b. Lily
c. Fern
d. Cycas

Answer 1

Hint: A flower is symmetrical when each whorl consists of an equal number of parts or when the parts of anyone whorl are multiples of that preceding it. In trimerous symmetry, there is an arrangement in flower parts such as petals, sepals, and stamens, in sets of three.

Complete answer:
- Floral symmetry describes if and how a flower, in particular its perianth, can be divided into two or more identical or mirror-image parts.
- Monocotyledon plants are said to have trimerous symmetry.
- Lily belongs to the family Liliaceae. Lily is considered as an actinomorphic flower.
- Lily has a trimerous flower which means that it has six petals, six stamens, and six carpels.
- All lily flowers are symmetrical but the petals come in different shapes, and also differ in the hybrid division. Some lilies have reflexed petals, each petal curves backward.

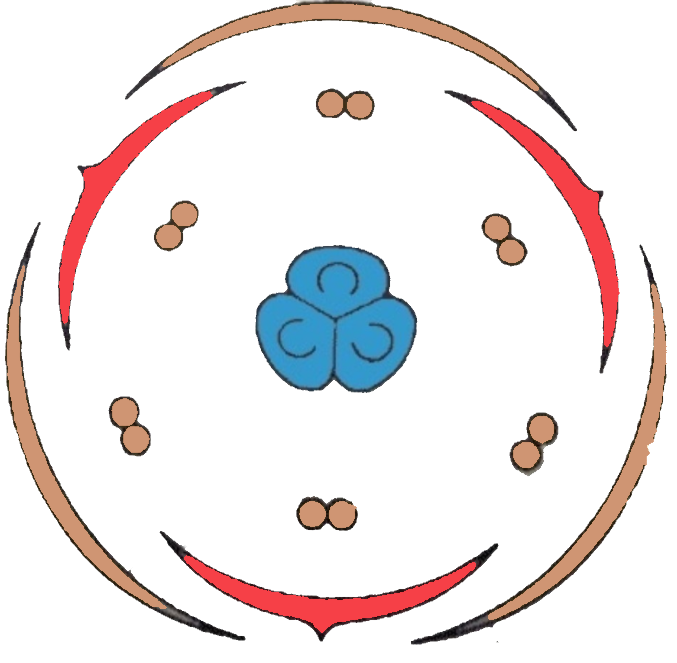
In the diagram showing above we can see that the flower is having three similar segments or parts. The set of petals, sepals, and stamens are three.

Hence, The correct answer is option (B).

Additional information:
Flowers can be zygomorphic or actinomorphic based on their symmetry. Zygomorphic flowers are those which are divided into two equal planes whereas, in Actinomorphic flowers, flowers are dissected into two mirror images, even dissected from any plane.
Lily is a trimerous, actinomorphic, polyandrous, superior ovary, and axile placentation.
A cacti plant does not have trimerous symmetry. Plants of fern and cycad do not bear flowers, hence no trimerous symmetry.

Note: Trimerous symmetry is found in Monocots. Lily is a monocotyledonous plant characterized by parallel leaf venation, leaves are linear in shape, single or arranged in a rosette. Flowers can be distinguished based on other types of symmetry, namely radial symmetry, bilateral symmetry, and asymmetrical.