Question

Which graph represents the uniform acceleration?
A.

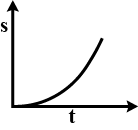
B.

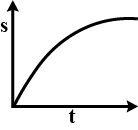
C.

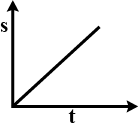
D.

Answer 1

Hint: Acceleration is defined as the rate of change of speed with time. Any change in the velocity of an object will cause an acceleration. Increasing speed is what we usually mean when it is said as acceleration, decreasing speed which is also called deceleration or retardation, or changing direction known as centripetal acceleration.

Complete step by step answer:
First of all let us take a look at what actually the uniform acceleration means. If an object's speed or velocity is increasing at a constant rate then we can say that it has uniform acceleration. The rate of acceleration is similar. If a car speeds up then slows down then speeds up then we can assume that car is not having a uniform acceleration.
Here in this question, it is given that acceleration is constant or the body moves with a uniform acceleration. Therefore we write that,
Acceleration=a=constant.
Hence we can write that,
$dV=adt$
Let us integrate this,
$\begin{align}
  & \int\limits_{u}^{v}{dv}=a\int\limits_{0}^{t}{dt} \\
 & \left[ v \right]_{u}^{v}=a\left[ t \right]_{0}^{t} \\
\end{align}$
That means $S=\dfrac{1}{2}a{{t}^{2}}$
$\begin{align}
  & \left[ v-u \right]=at \\
 & v=u+at \\
\end{align}$
And also we know that,
$ds=vdt$
This should be integrated,
$\int\limits_{0}^{s}{ds=\int\limits_{0}^{t}{udt+a\int\limits_{0}^{t}{tdt}}}$
Integrating this will give,
$S=ut+\dfrac{1}{2}a{{t}^{2}}$
Therefore as per the relation obtained we can say that, the graph should be a parabola which should be symmetric about the x-axis.
Hence we can see that option A is the right one when
$u=0$
And then
$S=\dfrac{1}{2}a{{t}^{2}}$

So, the correct answer is “Option A”.

Note: A body with a velocity zero can still accelerate. The simplest example is an object which is thrown upwards. At the highest point its velocity will become zero but will still accelerate due to the acceleration of gravity. The direction of the acceleration will decide whether you should add (positive acceleration) or subtract (negative acceleration).