Question

Which atom/ group is in the axial position?

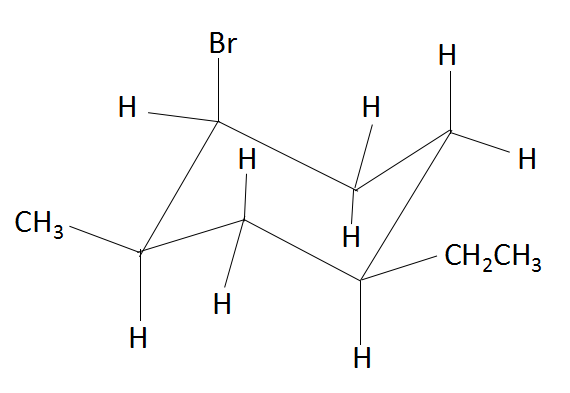
A. Bromine
B. Methyl
C. Ethyl
D. All of the above

Answer 1

Hint: The cyclohexane is a six carbon containing closed cycloalkane ring with a molecular formula of ${C_6}{H_{12}}$ . As the bond angle in the hexagonal structure of cyclohexane is ${60^o}$ , it experiences great torsional strain and due to which, it changes its conformation to a more stable boat form. The substituents which are along the plane are said to be in equatorial position and the substituents that lie perpendicular to the plane are said to be in axial position.

Complete step by step answer:
The torsional strain in the cyclohexane would be considered because all of the bonds would be in eclipsed form. Therefore, to reduce torsional strain, cyclohexane adopts a three-dimensional structure known as the chair conformation, which rapidly interconvert at room temperature via a process known as a chair flip. Due to this chair flip, the substituents on the cyclohexane ring get arranged either in the equatorial plane of the ring or in the axial position (perpendicular to the ring). In the above compound, the atoms that are present in the axial position are hydrogen and bromine. In the structure below, we find the various positions of axial and equatorial groups in a cyclohexane compound.

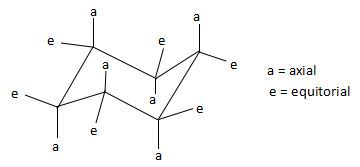
Thus, comparing the above structure and the structure in the question, we find that the group that is present in the axial position is bromine. Rest of the groups that are mentioned in the options are present in the equatorial position.

So, the correct answer is Option A .

Note:
The six- vertex edge ring does not conform to the shape of a perfect hexagon in free space as the carbon atoms are still $s{p^3}$ hybridised. The conformation of a flat 2D planar hexagon has a considerable large amount of angle strain because its bonds are not ${109.5^o}$ . In this case, the torsion experienced by the molecule of cyclohexane will be equal to = $\dfrac{{{{109.5}^o} - {{60}^o}}}{2} = {24.75^o}$ .