Question

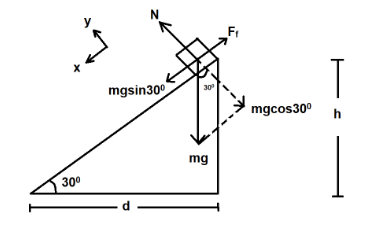
What is the acceleration of the box?

Answer 1

Hint: We know that total force on an object remains zero. Here, we will take the box as the object and then will equate all the forces acting on it.

Formulae Used: $ F = ma $
Where, $ F $ is the force on the object, $ m $ is its mass and $ a $ is its acceleration.
$ tan\theta = p/b $
Where, $ \theta $ is the angle of inclination, $ p $ is the perpendicular height and $ b $ is the base length.

Complete Step By Step Solution
Let us assume that the box accelerate down the slope,
Then, We know that Frictional Constant, $ \mu = tan\theta $
Here, $ \theta = {30^0} $
Thus, After calculating, we get
 $ \mu = 1/\surd 3 $
Now, $ mgsin{30^0} = {F_f} $
Also, $ {F_f} = \mu N $
But, N=mgcos300
 $ N = \surd 3mg $
Now, $ ma = {F_f} $
Thus, $ mgsin{30^0} = ma $
We know, $ g = 9.81m{s^{ - 2}} $
Thus, $ a = g \times \left( {1/2} \right) $
After calculating, we get
 $ a = 4.905m{s^{ - 2}} $
Thus, the acceleration of the box is $ 4.905{\text{ }}m{s^{ - 2}} $ .

Additional Information
The diagram we dealt upon is known as free body diagram in scientific terminology. It is actually a schematic representation of a real life problem taking into account the relative magnitudes and force acting on an object in a given situation.
The frictional constant $ \mu $ multiplied by the mass of the target object is the value up till which the object is acted upon by static friction and beyond this barrier the friction gets converted into kinetic friction. The value of kinetic friction is a bit lower than that of the static friction. In other words, we can say that the barrier is after which a body starts to move.

Note
The value we calculated is by taking $ g = 9.81m{s^{ - 2}} $ , but we could also approximate and take $ g = 10m{s^{ - 2}} $ . For that the value of acceleration comes out to be $ 5m{s^{ - 2}} $ .