Question

What are conservative forces?

Answer 1

HintConservative force has a property that work done in moving a particle between two points is independent of the path taken.

Complete step-by-step solution:The work done by such forces
Does not depend upon path.
Depends only and only initial and final position.
For example:- If A and B are the two points and a conservative force acts on point A and B. Then we assume the three ways to go at point B . 1,2 and 3 are the three ways.
  

If the force is conservative, then work done by this force by first path, by second path and third path are equal.
Let \[{{W}_{1}}\] be the work done along path 1, ${{W}_{2}}$ be the work done along path 2 and ${{W}_{3}}$ be the work done along path 3
Then,
${{W}_{1}}={{W}_{2}}={{W}_{3}}$
Examples of conservative forces are gravitational force , spring force, and electrostatic force.
First we talk about gravitational force, let us assume $\left( m \right)$ .Which is placed on an inclined plane.
For path 1:-
Angle between force $\left( mg \right)$ and displacement $\left( l \right)$ is$\left({{90}^{\circ }}+\theta \right)$

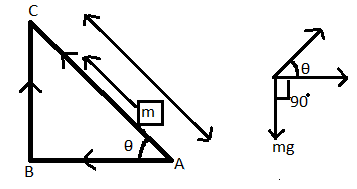
Than $\begin{align}
& {{W}_{1}}=FS\cos \phi \\
& {{W}_{1}}=mgl\left( \cos \left( {{90}^{\circ }}+\theta \right) \right) \\
& \\
\end{align}$ $\left[ \cos \left( {{90}^{\circ }}+\theta \right)=-\sin \theta \right]$
${{W}_{1}}=-mgl\sin \theta $ …………………..(i)
For path 2
First we go from point A to point B and then from point B to point C.
$W={{W}_{AB}}+{{W}_{BC}}$
When we go from A to B then the angle between force and displacement is ${{90}^{\circ }}$ $\left( \cos {{90}^{\circ }}=0 \right)$ .
Than $\begin{align}
 & {{W}_{AB}}=FS\cos {{90}^{\circ }} \\
 & {{W}_{AB}}=0 \\
\end{align}$
When we go from point B to C then the angle between force and displacement is ${{180}^{{}^\circ }}$.
${{W}_{BC}}=-mgl\sin \theta $
${{W}_{2}}={{W}_{AB}}+{{W}_{BC}}$
${{W}_{2}}=-mgl\sin \theta $ ……………….. (ii)
${{W}_{1}}={{W}_{2}}$
So the work done in the first path is equal to work done in the second path. So it is independent of path.

Note:
Students think that whose path has long distance then work done is maximum for that path, but for conservative force work done does not depend on path distance.