What are Complementary angles?
Answer
Verified604.5k+ views
Hint: In this question you will understand how to identify a complementary angles and know their applications in real life and also you will know how type of questions you may be asked in this concept but first we must know complementary angles are those angles whose sum adds up to ${90^ \circ }$.
Complete step-by-step answer:
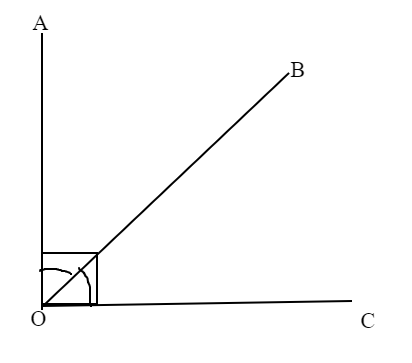
These are those angles whose sum adds up to ${90^ \circ }$. Also we must know that each of the angles is an acute angle. Acute angles are those angles whose value is less than ${90^ \circ }$ and as a fact these angles’ sum never exceed ${180^ \circ }$. Complementary angles always consist of two angles.
Three or more angles whose sum adds up to ${90^ \circ }$will not be considered as complimentary. Complementary angles may or may not be in pairs as it is not necessary for them to be in a pair they can occur as different angles too. Complementary angles can be found in some designs of buildings and carpenters use a device called ‘miter joint’ which is made by this principle.
Complementary angles sum never exceeds ${90^ \circ }$and if in some question it does then they may not be complementary angles. These angles are referred to as compliments of each other as they add up to ${90^ \circ }$. These angles occur very frequently in some questions where you may be asked to find the complement of another angle.
In such questions just take the other angles as ‘x’ and put their sum equal to ${90^ \circ }$ and also one must be aware that in other types of questions these angles will even be in pairs so do use the above mentioned way of finding the solution. We must know that any two angles in any situation adding up to ${90^ \circ }$ will be complementary angles. These angles are pretty easy to identify as you know in every figure their sum will add up to ${90^ \circ }$. Thus you can mention this reason in any question if two angles add up to ${90^ \circ }$.
Note: To be noted that we learnt about complementary angles as we know those angles whose sum adds up to ${90^ \circ }$ and as we know these angles are always two in number not anything more than that. These angles also have some applications in real life like a device called miter joint used by carpenters. We must also know in mathematics solutions to such questions as in complementary angles is given by making an equation whose sum adds up to ${90^ \circ }$but we also must know one of the values is always given. So these angles form an integral part of mathematics.
Complete step-by-step answer:
These are those angles whose sum adds up to ${90^ \circ }$. Also we must know that each of the angles is an acute angle. Acute angles are those angles whose value is less than ${90^ \circ }$ and as a fact these angles’ sum never exceed ${180^ \circ }$. Complementary angles always consist of two angles.
Three or more angles whose sum adds up to ${90^ \circ }$will not be considered as complimentary. Complementary angles may or may not be in pairs as it is not necessary for them to be in a pair they can occur as different angles too. Complementary angles can be found in some designs of buildings and carpenters use a device called ‘miter joint’ which is made by this principle.
Complementary angles sum never exceeds ${90^ \circ }$and if in some question it does then they may not be complementary angles. These angles are referred to as compliments of each other as they add up to ${90^ \circ }$. These angles occur very frequently in some questions where you may be asked to find the complement of another angle.
In such questions just take the other angles as ‘x’ and put their sum equal to ${90^ \circ }$ and also one must be aware that in other types of questions these angles will even be in pairs so do use the above mentioned way of finding the solution. We must know that any two angles in any situation adding up to ${90^ \circ }$ will be complementary angles. These angles are pretty easy to identify as you know in every figure their sum will add up to ${90^ \circ }$. Thus you can mention this reason in any question if two angles add up to ${90^ \circ }$.
Note: To be noted that we learnt about complementary angles as we know those angles whose sum adds up to ${90^ \circ }$ and as we know these angles are always two in number not anything more than that. These angles also have some applications in real life like a device called miter joint used by carpenters. We must also know in mathematics solutions to such questions as in complementary angles is given by making an equation whose sum adds up to ${90^ \circ }$but we also must know one of the values is always given. So these angles form an integral part of mathematics.
Recently Updated Pages
Trending doubts
Who was the first woman to receive Bharat Ratna?
Who Won 36 Oscar Awards? Record Holder Revealed
State and prove the Pythagoras theorem-class-10-maths-CBSE
State BPT theorem and prove it class 10 maths CBSE
What is the minimum age for fighting the election in class 10 social science CBSE
Describe the Salient Features of Indian Economy