Question

Velocity $(v)$-Time $(t)$ graph of a body thrown vertically upward is:
A. A straight line
B. A parabola
c. A hyperbola
D. A circle

Answer 1

Hint:In order to answer this question let us have some idea about motion of kinematics. Kinematics is a branch of classical mechanics that deals with the motion of points, structures, and systems of objects without taking into account the causes of motion (i.e., forces. The "geometry of motion" is a term used to describe kinematics.

Complete answer:
When a body is tossed vertically upward, it experiences a relentless acceleration. By using,
$\overrightarrow v = \overrightarrow u + \overrightarrow a t$
Let initial velocity be$u$upward ,$g$ is acting downwards
$\overrightarrow v = u - gt$ upwards

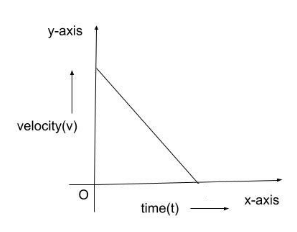
This is a slope- $g$ based equation for a straight line.

So, the correct option is A.

Additional Information:
Slope of velocity $(v)$-time $(t)$ graph the graph is equal to acceleration. This implies that when the slope is steep, the object's velocity will change quickly. When the slope is shallow, the object's velocity does not change as quickly. This also implies that the acceleration would be negative if the slope is negative (directed downwards), and positive if the slope is positive (directed upwards).

Note:The object's acceleration is represented by the slope of a velocity graph. As a result, the value of the slope at a given time reflects the object's acceleration at that time. The slope is defined as the ratio of y-axis change to x-axis .