Question

Vector \[\overset{\to }{\mathop{A}}\,\] of magnitude 4 units is directed along the positive X-axis. Another vector \[\overset{\to }{\mathop{B}}\,\] of magnitude 3 units lies in the X-Y plane and its directed along \[30{}^\circ \]with the positive X-axis. The \[\overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,\] is ____.
\[\begin{align}
  & A.\,6\,units \\
 & B.\,6\sqrt{2}\,units \\
 & C.\,6\sqrt{3}\,units \\
 & D.\,12\,units \\
\end{align}\]

Answer 1

Hint: Consider the right handed coordinate system to draw the vectors. It becomes easier to compute the values considering the diagram representing the placing of the vectors. Vector A value has an i component. The components of vector B are not given directly, so, we will compute the components of i and j. Finally, we will compute the dot product of the vectors.

Complete step by step answer:
From the given information, we have the data as follows.
Vector \[\overset{\to }{\mathop{A}}\,\] of magnitude 4 units is directed along the positive X-axis. Another vector \[\overset{\to }{\mathop{B}}\,\] of magnitude 3 units lies in the X-Y plane and its directed along \[30{}^\circ \]with the positive X-axis.
The diagram representing the vectors A and B is given as follows.

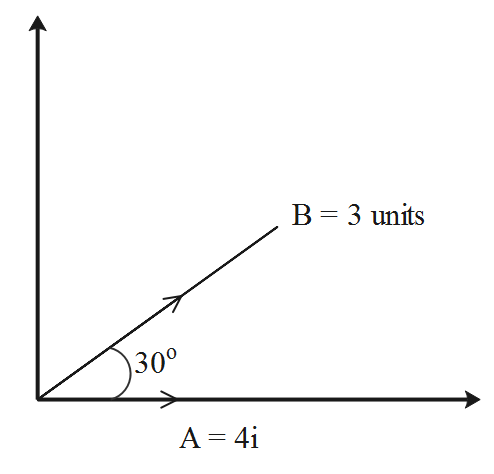
Consider vector A.
The component of the vector A along the x-axis is, \[{{\overset{\to }{\mathop{A}}\,}_{x}}=4i\].
The component of the vector A along the y-axis is, \[{{\overset{\to }{\mathop{A}}\,}_{y}}=0j\].
Therefore, the representation of the vector A in terms of its components is, \[\overset{\to }{\mathop{A}}\,=4i\]
Consider vector B.
The component of the vector B along the x-axis is,
 \[\begin{align}
  & {{\overset{\to }{\mathop{B}}\,}_{x}}=3\cos 30{}^\circ \\
 & \Rightarrow {{\overset{\to }{\mathop{B}}\,}_{x}}=3\times \dfrac{\sqrt{3}}{2} \\
 & \therefore {{\overset{\to }{\mathop{B}}\,}_{x}}=\dfrac{3\sqrt{3}}{2}i \\
\end{align}\].
The component of the vector B along the y-axis is,
\[\begin{align}
  & {{\overset{\to }{\mathop{B}}\,}_{y}}=3\sin 30{}^\circ \\
 & \Rightarrow {{\overset{\to }{\mathop{B}}\,}_{y}}=3\times \dfrac{1}{2} \\
 & \therefore {{\overset{\to }{\mathop{B}}\,}_{y}}=\dfrac{3}{2}j \\
\end{align}\].
Therefore, the representation of the vector B in terms of its components is, \[\overset{\to }{\mathop{B}}\,=\dfrac{3\sqrt{3}}{2}i+\dfrac{3}{2}j\]
Now, we will compute the dot product of the vectors A and B.
Consider the computation.
\[\begin{align}
  & \overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,=(4i).\left( \dfrac{3\sqrt{3}}{2}i+\dfrac{3}{2}j \right) \\
 & \therefore \overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,=(4i).\left( \dfrac{3\sqrt{3}}{2}i \right) \\
\end{align}\]
We know that \[i.i=1\] and \[i.j=0\]
Thus, the value of the dot product is,
\[\therefore \overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,=6\sqrt{3}\,units\]
\[\therefore \] The value of the dot product of the vectors A and B is,\[6\sqrt{3}\,units\]

So, the correct answer is “Option C”.

Note: There are two methods of computing the product of vectors, one being the dot product and other being the vector product. The result of the dot product is scalar quantity and the result of the vector product is vector quantity.