Question

Two vertices of a triangle are $ (4, - 3) $ and $ ( - 2,5) $ . If the orthocentre of the triangle is at $ (1,2) $ . Then the third vertex is

Answer 1

Hint: As we know that the orthocentre of a triangle is the point of intersection of altitudes of the triangle. Here in this question we will assume the third vertex as $ (x,y) $ . We should know that to find the slope of the line having two points $ ({x_1},{y_1}) $ and $ ({x_2},{y_2}) $ , we use this formula $ m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ .

Complete step-by-step answer:

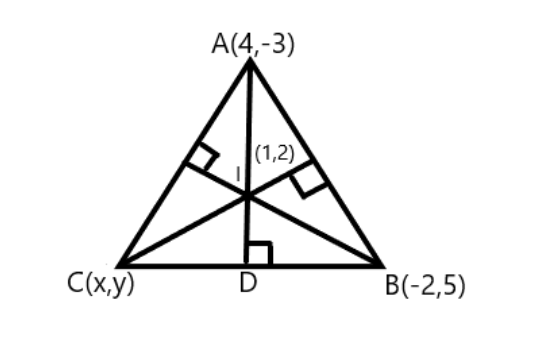
Here let us assume the third vertex be $ C = (x,y) $ .
Then we have $ A = (4, - 3),B = ( - 2,5) $ . We have the orthocentre i.e. $ I = (1,2) $ .
So we can say that the slope of AB is $ \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ .
 Here by comparing we have $ {y_2} = 5,{y_1} = - 3,{x_2} = - 2,{x_1} = 4 $ .
By putting the values in the formula we have AB $ = \dfrac{{5 - ( - 3)}}{{ - 2 - 4}} = \dfrac{{ - 4}}{3} $ .
Similarly we will calculate the slope of IC i.e. $ \dfrac{{y - 2}}{{x - 1}} $ . We will now equate both the expressions and we have $ \dfrac{{y - 2}}{{x - 1}} = \dfrac{3}{4} $ .
By cross multiplication we have $ 4(y - 2) = 3(x - 1) $ . By breaking the brackets we have $ 4y - 8 = 3x - 3 $ .
We can write this in the form of the linear equation i.e. $ 3x - 4y + 5 = 0 $ .
Again we have to calculate the slope of AC.
 Here by comparing we have $ {y_2} = y,{y_1} = - 3,{x_2} = x,{x_1} = 4 $ .
By putting the values in the formula we have AC $ = \dfrac{{y - ( - 3)}}{{x - 4}} = \dfrac{{y + 3}}{{x - 4}} $ .
For IB we have points $ B = ( - 2,5) $ and $ I = (1,2) $ . By comparing we have $ {y_2} = 5,{y_1} = 2,{x_2} = - 1,{x_1} = 1 $ .
Similarly we will calculate the slope of IB i.e.
$ \dfrac{{5 - 2}}{{ - 2 - 1}} = - 1 $ .
We will now equate both the expressions and we have $ \dfrac{{y + 3}}{{x - 4}} = 1 $ .
By cross multiplication we have
$ y + 3 = x - 4 \Rightarrow x - y - 7 = 0 $ .
So we have two equations i.e.
$ x - y - 7 = 0 $ and $ 3x - 4y + 5 = 0 $ .
WE can solve this by elimination method i.e. by multiplying the first equation with $ 3 $ , and then we subtract the second equation, we can write
$ 3x - 3y - 21 - 3x + 4y - 5 = 0 $ .
On further solving we have
$ 4y - 3y = 21 + 5 \Rightarrow y = 26 $ .
Putting this value in the first equation we have
$ x - 26 - 7 = 0 \Rightarrow x = 33 $ .
Hence the third vertex is $ (26,33) $ .
So, the correct answer is “ $ (26,33) $ .”.

Note: Before solving this kind of question we should have the full knowledge of the orthocentre, slope of the lines and their formulas. We should note that the equation of the ;line passing through a point $ (x,y) $ with slope $ m $ can be written as $ y - y' = m(x - x') $ . We should avoid calculation mistakes while solving the equations.