Question

Two spheres A and B of the same mass m and the same radius are placed on a rough horizontal surface A is a uniform hollow sphere and B is a uniform solid sphere. A and B can roll without sliding on the floor. They are also tied centrally to a light spring of spring constant k. A and B are released when the extension in the spring is \[{{x}_{0}}\].

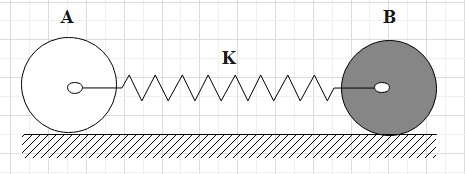
A) Find the amplitude of SHM of the sphere B
\[A.\,\dfrac{25{{x}_{0}}}{46}\]
\[B.\,\dfrac{21{{x}_{0}}}{46}\]
\[C.\,\dfrac{27{{x}_{0}}}{46}\]
\[D.\,\dfrac{27{{x}_{0}}}{46}\]

B) Find the frequency of oscillation of the spheres.
\[A.\,\dfrac{1}{2\pi }\sqrt{\dfrac{35k}{46m}}\]
\[B.\,\dfrac{1}{2\pi }\sqrt{\dfrac{46k}{35m}}\]
\[C.\,\dfrac{1}{2\pi }\sqrt{\dfrac{25k}{46m}}\]
\[D.\,\dfrac{1}{2\pi }\sqrt{\dfrac{21k}{46m}}\]

Answer 1

Hint: Firstly, the displacements of the spheres should be considered. The formulae for calculating the inertia and the torque should be used. Following, the angular momentum should be conserved. By using all the equations obtained, we need to derive the expressions for the amplitude of SHM of sphere B and the frequency of oscillation of the spheres.

Formula used:
\[\begin{align}
  & I=\dfrac{5}{3}M{{R}^{2}} \\
 & \tau =I\alpha \\
\end{align}\]

Complete step by step answer:
Consider the sphere A with the mean displacement of \[{{x}_{1}}\] has moved towards the left. Similarly, the sphere B with the mean displacement of \[{{x}_{2}}\] has moved towards the right. Consider the below figure.

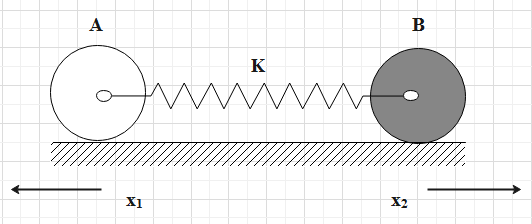
Therefore, the value of the total extension will be equal to the value given by,
Total extension = \[{{x}_{1}}+{{x}_{2}}\].
Now we need to find the expression for the torque in terms of the momentum. Thus, we have,
The torque of A is given as follows.
\[{{\tau }_{A}}={{I}_{A}}{{\alpha }_{A}}\]
Now substitute the expressions of the torque and moment of inertia of a hollow sphere in the above equation. Therefore, we get,
\[K({{x}_{1}}+{{x}_{2}})r=\left( \dfrac{5}{3}m{{r}^{2}} \right){{\alpha }_{A}}\]
 Cancel out the common terms
\[K({{x}_{1}}+{{x}_{2}})=\dfrac{5}{3}m(r{{\alpha }_{A}})\]
Where \[{{\alpha }_{A}}\] is the angular acceleration, thus, \[r{{\alpha }_{A}}\] will become linear acceleration.
So, we have,
\[K({{x}_{1}}+{{x}_{2}})=\dfrac{5}{3}m{{a}_{A}}\] …… (1)
Consider the moment of inertia of the solid sphere as well.
The angular momentum needs to be conserved. So, we get,
\[\dfrac{5}{3}m{{v}_{1}}r=\dfrac{7}{5}m{{v}_{2}}r\]
\[\Rightarrow 25{{v}_{1}}=21{{v}_{2}}\]
The \[{{v}_{1}}=\dfrac{d{{x}_{1}}}{dt},{{v}_{2}}=\dfrac{d{{x}_{2}}}{dt}\], so, we can write the above equation as,
\[25{{x}_{1}}=21{{x}_{2}}\]
Represent the above equation in terms of \[{{x}_{2}}\], so, we have,
\[{{x}_{2}}=\dfrac{25}{21}{{x}_{1}}\] ….. (2)
Substitute the equation (2) in the equation (1), so, we get,
\[K\left( {{x}_{1}}+\dfrac{25}{21}{{x}_{1}} \right)=\dfrac{5}{3}m{{a}_{A}}\]
Further continue the calculation.
\[\begin{align}
  & \dfrac{46k{{x}_{1}}}{21}=\dfrac{5}{3}m{{a}_{A}} \\
 & \Rightarrow {{a}_{A}}=\dfrac{46}{35}\dfrac{k}{m}{{x}_{1}} \\
\end{align}\]
In terms of displacement, we get the above equation as follows.
\[-\dfrac{{{d}^{2}}{{x}_{1}}}{d{{t}^{2}}}=\dfrac{46}{35}\dfrac{k}{m}{{x}_{1}}\]…… (a)
The negative sign indicates the opposite direction of the displacement compared to that of the acceleration.
The above equation represents the acceleration given by the standard form as follows.
\[\dfrac{{{d}^{2}}x}{d{{t}^{2}}}=-{{w}^{2}}{{x}_{1}}\]….. (b)
Upon comparing the equations (a) and (b) we can find the expression in terms of the angular frequency.
\[\begin{align}
  & {{w}^{2}}=\dfrac{46}{35}\dfrac{k}{m} \\
 & \Rightarrow w=\sqrt{\dfrac{46}{35}\dfrac{k}{m}} \\
\end{align}\]
The frequency is given by the formula.
\[\begin{align}
  & f=\dfrac{1}{2\pi }w \\
 & \Rightarrow f=\dfrac{1}{2\pi }\sqrt{\dfrac{46}{35}\dfrac{k}{m}} \\
\end{align}\]
Therefore, the frequency of oscillation of the spheres is \[\dfrac{1}{2\pi }\sqrt{\dfrac{46}{35}\dfrac{k}{m}}\].
The sum of the amplitudes of the spheres A and B will be equal to \[{{x}_{0}}\], because of the maximum position reached by the spheres A and B. So, we get,
\[{{x}_{0}}={{x}_{A}}+{{x}_{B}}\]
As the relation between the displacements is \[{{x}_{2}}=\dfrac{25}{21}{{x}_{1}}\], thus, the same relationship applies to the amplitudes of the spheres A and B.
\[\begin{align}
  & {{x}_{0}}=\dfrac{21}{25}{{x}_{B}}+{{x}_{B}} \\
 & \Rightarrow {{x}_{0}}=\dfrac{46}{25}{{x}_{B}} \\
\end{align}\]
Rearrange the terms of the above equation.
\[{{x}_{B}}=\dfrac{25}{46}{{x}_{0}}\]
Therefore, the amplitude of SHM of the sphere B is \[\dfrac{25}{46}{{x}_{0}}\].

Therefore, the amplitude of SHM of sphere B is \[\dfrac{25}{46}{{x}_{0}}\], thus, the option (A) is correct.
Therefore, the frequency of oscillation of the spheres is \[\dfrac{1}{2\pi }\sqrt{\dfrac{46}{35}\dfrac{k}{m}}\], thus, the option (B) is correct.

Note: In this case, the amplitude of SHM of the sphere B is asked, even they can ask for the amplitude of SHM of the sphere A. in that case, represent the value of displacement of the sphere B in terms of the displacement of sphere A. The frequency of oscillation of the spheres is asked, even, they may ask for the time period. In such a case, just reverse the expression of the frequency of oscillation of the spheres.