Question

Two small, identical spheres having $+Q$ and $-Q$ charge are kept at a certain distance. $F$ force acts between the two. If in the middle of two spheres, another similar sphere having $+Q$ charge is kept, then it experiences a force in magnitude and direction as
(A) Zero having no direction
(B) $8\;F$ towards $+Q$ charge
(C) $8\;F$ towards $-Q$ charge
(D) $4\;F$ towards $+Q$ charge

Answer 1

Hint: Here the force between two oppositely charged spheres is given as $F$. If we introduce another sphere of positive charge in the middle of the two spheres there will be a force on the new sphere due to the other two spheres. We have to find the magnitude and direction of force acting on the newly introduced sphere using coulomb’s law.

Formula used:
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Where $F$ stands for the force due to the two charges, ${q_1}$ and ${q_2}$ stands for the two charges, $r$ stands for the separation between the two charges and ${\varepsilon _0}$ stands for the permittivity of free space.

Complete step by step solution:
The force between two charges separated by a distance can be found using Coulomb’s law.
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Let the charge of the first sphere be ${q_1} = + Q$
Let the charge of the second sphere be ${q_2} = - Q$
Let the two charges be separated by a distance $r$
When a sphere of $ + Q$ charge is introduced in the middle of the two charges,
As shown in the figure

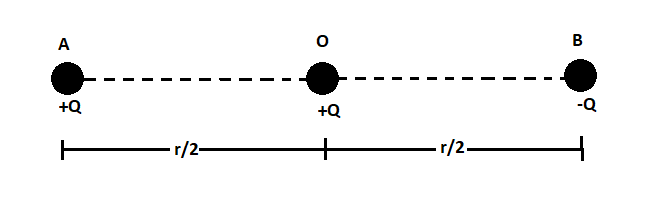
The positive charge $A$ will repel the sphere $O$ and the negative sphere $B$ will attract the sphere $O$
Therefore the direction will be towards the negative charge.
The force between the two spheres $A$ and $B$ can be written as,
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{QQ}}{{{r^2}}}$
This can be written as
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{r^2}}}$
The force acting on the third sphere due to the positive sphere can be written as
${F_{AO}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{QQ}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}}$
This can be written as,
${F_{AO}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{4{Q^2}}}{{{r^2}}} = 4F$
The force acting on the third sphere due to the negatively charged sphere can be written as,
${F_{OB}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{QQ}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{4{Q^2}}}{{{r^2}}} = 4F$
The total charge on the sphere can be written as,
${F_{total}} = {F_{AO}} + {F_{OB}}$
Substituting the values we get,
${F_{total}} = 4F + 4F = 8F$
We already found that the direction is towards the negative charge.
Therefore,
The answer is: Option (C): $8\;F$ towards $ - Q$ charge.

Note:
The magnitude of Coulomb force will depend on the quantity of charges, distance between the charges and the nature of the medium. If the charges are similar then the Coulomb force between them will be positive and it is repulsive in nature. If the charges are opposite then the coulomb charge will be negative and attractive in nature.