Question

Two sides of a parallelogram are along the lines \[x+y=3\] and \[x-y+3=0\]. If its diagonals
intersect at \[(2,4)\], then one of its vertex is
(a) \[(2,6)\]
(b) \[(2,1)\]
(c) \[(3,5)\]
(d) \[(3,6)\]

Answer 1

Hint: Solve the 2 line equations to find the coordinates of intersection of these 2 lines and use section formula to find the remaining coordinates of a parallelogram.

The equations given in the question are,
\[x+y=3\] and \[x-y+3=0\]
They can be rewritten as,
\[x+y=3\] and \[x-y=-3\]
Also, it is given that the diagonals intersect at \[(2,4)\]. Draw the parallelogram representing the given data as shown below,

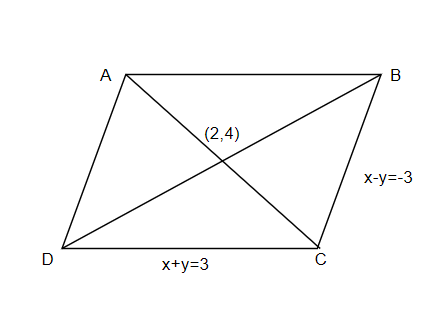
AThe vertex C is a point that intersects the lines DC and BC. Therefore, the coordinates of the C can be obtained by adding and solving the two equations of the lines as below,
\[\dfrac{\begin{align}
  & x+y=3 \\
 & x-y=-3 \\
\end{align}}{\begin{align}
  & 2x=0 \\
 & x=0 \\
\end{align}}\]
Substituting the value of \[x\], we have the value of \[y\] as,
\[\begin{align}
  & 0+y=3 \\
 & \Rightarrow y=3 \\
\end{align}\]
Therefore, the coordinates of C are \[(0,3)\].
The coordinates of vertex B can be obtained by supposing \[x=p\]in the equation \[x-y=-3\]. So, we have the coordinates as \[(p,3+p)\]. To get the coordinates of vertex D, suppose \[x=q\]in the equation \[x+y=3\]. So, we have the coordinates as \[(q,3-q)\]. Let the coordinates of vertex A be \[(m,n)\]. The figure can be redrawn with the above details as below,

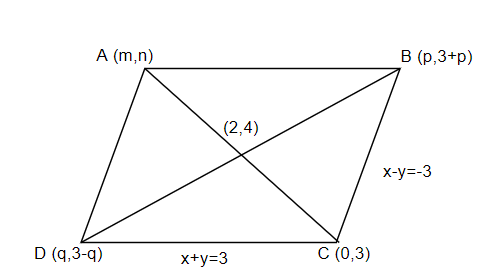
The coordinates of the point of intersection of the diagonals are given as \[(2,4)\]. The point of intersection is the midpoint of the line AC as well as the line BD. It divides the lines in the ratio \[1:1\].
Using the section formula, the coordinates of vertex A \[(m,n)\] can be found as,
\[\left( \dfrac{m+0}{2},\dfrac{n+3}{2} \right)=\left( 2,4 \right)\]
Equating both coordinates on either sides,
\[\begin{align}
  & \dfrac{m}{2}=2,\dfrac{n+3}{2}=4 \\
 & m=4,n=(8-3) \\
 & m=4,n=5 \\
\end{align}\]
Therefore, coordinates of A are \[(4,5)\].
Using section formula to find the coordinates of D and B,
\[\begin{align}
  & \left( \dfrac{p+q}{2},\dfrac{3+p+3-q}{2} \right)=(2,4) \\
 & \left( \dfrac{p+q}{2},\dfrac{p-q+6}{2} \right)=(2,4) \\
\end{align}\]
Equating both coordinates on either sides,
\[\begin{align}
  & p+q=4,p-q=(8-6) \\
 & p+q=4,p-q=2 \\
\end{align}\]
We get two equations \[p+q=4\] and \[p-q=2\]. Adding and solving the two equations,
\[\dfrac{\begin{align}
  & p+q=4 \\
 & p-q=2 \\
\end{align}}{\begin{align}
  & 2p=6 \\
 & p=3 \\
\end{align}}\]
Substituting the value of \[p\], we have the value of \[q\] as,
\[\begin{align}
  & 3+q=4 \\
 & q=1 \\
\end{align}\]
Now, re-substituting these values, we can get the coordinates of B and D as,
B\[(p,3+p)\Rightarrow (3,3+3)=(3,6)\]
D\[(q,3-q)\Rightarrow (1,3-1)=(1,2)\]
Looking at the options, the only possible answer is the coordinates of B, which is \[(3,6)\].
Therefore, we get option (d) as the correct answer.
Note: One way in which this problem could go wrong is by interchanging the coordinates of B and D which are written in terms of \[p\] and \[q\]. If you write the coordinates as \[(3+p,p)\] and \[(3-q,q)\] instead of \[(p,3+p)\]and \[(q,3-q)\], you might end up getting the coordinates as \[(6,3)\] and \[(2,1)\] and choose the wrong option.