Question

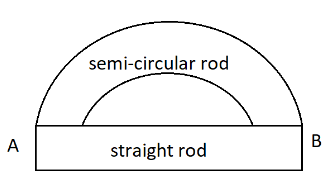
Two rods (one semicircular and other straight) of the same material and same cross-sectional area are joined as shown in the figure. The points $A$ and $B$ are maintained at a different temperature. The ratio of heat transferred through a cross-section of the semicircular rod to heat transferred through a cross-section of the straight rod in a given time is:

A. $\left( a \right){\text{ 2:}}\pi $
B. $\left( b \right){\text{ 1:2}}$
C. $\left( c \right){\text{ }}\pi :2$
D. $\left( d \right){\text{ 3:2}}$

Answer 1

Hint:The above problem is based on the concept of heat transfer. The heat transfer may occur by conduction, convection, or radiation. The heat transfer within the solid object or two different objects in contact occurs by the conduction. The transferred heat by the conduction depends on the thermal conductivity, the cross-section area of the objects, and temperature difference at different positions.

Complete step by step answer:
From the question we have,
The thermal conductivity of the semicircular and straight rod is ${K_1} = {K_2}$
The cross-sectional area of the semicircular and straight rod is ${A_1} = {A_2}$
Let us assume that the temperature of the semicircular rod is ${T_1}$ and that of the straight rod is ${T_2}$ , the radius of the semicircular rod is $R$ .
The expression to calculate the length of the semicircular rod is given as,
$ \Rightarrow {L_1} = \pi R$
The expression to calculate the length of the straight rod is given as,
$ \Rightarrow {L_2} = 2R$
The expression to calculate the heat transferred through semicircular rod is,
$ \Rightarrow {Q_1} = {K_1}{A_1}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_1}}}} \right)$ , and we will name it equation $1$
The expression to calculate the heat transferred through straight rod is,
 $ \Rightarrow {Q_2} = {K_2}{A_2}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_2}}}} \right)$ , and we will name it equation $2$
Divide the equation $1$ by equation $2$ to find the expression for ratios of heat transferred through a cross-section of the semicircular rod to heat transferred through a cross-section of the straight rod, we get
$ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{{K_1}{A_1}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_1}}}} \right)}}{{{K_2}{A_2}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_2}}}} \right)}}$
And since both are equal, therefore, that is ${K_1} = {K_2}$ and ${A_1} = {A_2}$ , we get
$ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{{K_1}{A_1}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_1}}}} \right)}}{{{K_1}{A_1}\left( {\dfrac{{{T_1} - {T_2}}}{{{L_2}}}} \right)}}$
And on solving the above equation we get
$ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{{L_2}}}{{{L_1}}}$
Now on substituting $\pi R$ for ${L_1}$ and $2R$ for ${L_2}$ to find the ratio of heat transferred through a cross-section of the semicircular rod to heat transferred through a cross-section of the straight rod, so we get
\[ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{2R}}{{\pi R}}\]
Since the like terms will cancel out each other, therefore we have
\[ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{2}{\pi }\]
And in the ratio, it can be written as
$ \therefore {Q_1}:{Q_2} = 2:\pi $
Thus, the ratio of heat transferred through a cross-section of the semicircular rod to heat transferred through a cross-section of the straight rod is $2:\pi $ .

Therefore, the option A is the correct answer.

Note:Here in this question we should be careful while taking the length of the rod and the semicircular rod which is not a full rod. So don’t create mistakes in a hurry by taking the length of the full circle. Also, we should know that the heat transferred by the conduction method can be found by using Fourier’s law of heat transfer.