Question

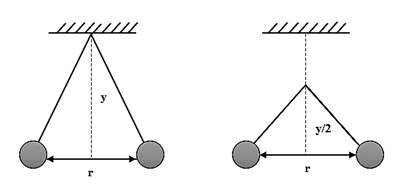
Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

$A. { \left( \dfrac { 1 }{ \sqrt { 2 } } \right) }^{ 2 }$
$B. \left( \dfrac { r }{ \sqrt [ 3 ]{ 2 } } \right)$
$C. \left( \dfrac { 2r }{ \sqrt { 3 } } \right)$
$D. \left( \dfrac { 2r }{ 3 } \right)$

Answer 1

Hint: To solve this problem, first draw the free body diagram. At equilibrium, the upward force is equal to the downward force and the force from left is equal to the force from right. So, equate these forces. Take the ratio of these equations and obtain the relation between y and r. We have to find the separation when y changes to y/2, so substitute this value in the above obtained relation and find the equilibrium separation when y changes to y/2.

Complete step-by-step solution:

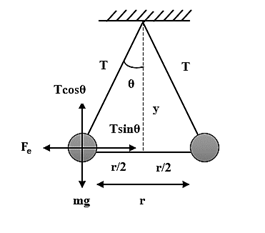
Let the tension on the string be T, Mass of the ball be m, Charge on the ball be q, Electric force be ${F}_{e}$.

At equilibrium,
$T\cos{\theta}= mg$ …(1)
$T\sin{\theta}= {F}_{e}$ …(2)

We know, according to Coulomb’s law, electric field is given by,
${F}_{e}= \dfrac {k{q}^{2}}{{r}^{2}}$ …(3)
Where, k is the Coulomb’s law constant

Substituting equation. (3) in equation.(2) we get,
$T\sin{\theta}=\dfrac {k{q}^{2}}{{r}^{2}}$ …(4)

Dividing equation. (4) by equation. (1) we get,
$\tan { \theta } =\dfrac { k{ q }^{ 2 } }{ mg{ r }^{ 2 } }$ …(5)

From the above figure, we get,
$\tan { \theta } =\dfrac {r }{ 2y }$ …(6)

Comparing equation. (5) and (6) we get,
$ \dfrac { k{ q }^{ 2 } }{ mg{ r }^{ 2 } } =\dfrac {r}{2 y }$

Rearranging the above equation we get,
$y=\dfrac { mg{ r }^{ 3 } }{ 2k{ q }^{ 2 } }$

From the above expression, we get y is directly proportional to the cube of r.
$\Rightarrow y \propto {r}^{3}$
$\Rightarrow r\propto { y }^{ \dfrac { 1 }{ 3 } }$ ...(7)

Thus, the equilibrium separation for $\dfrac {y}{2}$ can be given by,
${ r }^{ ' }\propto { \left( \dfrac { y }{ 2 } \right) }^{ \dfrac { 1 }{ 3 } }$
$\Rightarrow { r }^{ ' }\propto \dfrac { { y }^{ \dfrac { 1 }{ 3 } } }{ { 2 }^{ \dfrac { 1 }{ 3 } } }$

Substituting equation. (7) in above equation we get,
${ r }^{ ' }\propto \dfrac { r }{ { 2 }^{ \dfrac { 1 }{ 3 } } }$
$\Rightarrow { r }^{ ' }\propto \dfrac { r }{ \sqrt [ 3 ]{ 2 } }$

Thus, the equilibrium separation between the balls now becomes $ \dfrac { r }{ \sqrt [ 3 ]{ 2 } }$.

So, the correct answer is option B i.e. $\dfrac { r }{ \sqrt [ 3 ]{ 2 } }$.

Note:
To answer these types of questions, students must first draw the free body diagram which is also known as force body diagram. To draw a free body diagram, students must have knowledge of these diagrams. It is used to represent momentum and force applied on the object. It helps to represent the magnitude and direction of the forces. Also, there are a lot of equations in this solution, so students must take care of the equation numbers.