Question

Two particles projected from the same point with same speed u at angles of projection $\alpha$ and $\beta$ strike the horizontal ground at the same point. If $h_1$ and $h_2$ are the maximum heights attained by projectiles, R be the range for both and $t_1$ and $t_2$ be their time of flights respectively, then:
A.$\alpha +\beta = \dfrac{\pi}{2}$
B.$R=4\sqrt{h_1h_2}$
C.$\dfrac{t_1}{t_2} = tan\alpha$
D.$tan\alpha=\sqrt{\dfrac{h_1}{h_2}}$

Answer 1

Hint: We are dealing with a case of horizontal projectile motion. Note that multiple options may be correct. Recall the expressions for the horizontal distance travelled, the vertical height attained by each projectile, and the time of flight of the projectiles.
Since the two particles have the same range, equate the two ranges and determine the relation between their projection angles to verify the first option. Then, multiply the two vertical height expressions together under a square root and check for the validity of option B. Next, divide the two time of flight expressions and check for option C, and finally divide the two vertical height expressions under root to check for option D.
Formula Used:
Horizontal range $ R = \dfrac{u^2\;sin2\theta}{g}$
Vertical height $h = \dfrac{u^2\;sin^2\theta}{2g}$
Time of flight $t = \dfrac{2u\;sin\theta}{g}$

Complete answer:
Let us begin by first understanding the question given to us and then by listing out the parameters given to us.
The question basically deals with a case of projectile motion. Projectile motion is a form of motion where an object moves in a parabolic path. It occurs when there is one force that launches the object after which the only influencing force is gravity. The path that the object follows under this influence of gravity is called projectile trajectory. In most cases for our convenience, we neglect air resistance.
In general, the horizontal distance or range of a projectile is given by: $R = \dfrac{u^2\;sin2\theta}{g}$
The maximum height attained is given by: $h = \dfrac{u^2\;sin^2\theta}{2g}$, and
The time of flight of the projectile is given by: $t = \dfrac{2u\;sin\theta}{g}$
Let us now look into the context of our question.
Let the two projectiles be A and B, that are launched with the same velocity u and are subject to an acceleration due to gravity g.
The projection angles are $\theta_A =\alpha$ and $\theta_B = \beta$ respectively.
Let the horizontal distances travelled by them be given by the range:
$R_A = \dfrac{u^2\;sin2\alpha}{g}$ and $R_B = \dfrac{u^2\;sin2\beta}{g}$
They both have the same range R, i.e.,
$R = R_A = R_B \Rightarrow \dfrac{u^2\;sin2\alpha}{g}= \dfrac{u^2\;sin2\beta}{g}$
$\Rightarrow sin2\alpha=sin2\beta \Rightarrow 2\alpha = 2\beta \Rightarrow \alpha = \beta $.
Suppose we were to visualize this motion on a co-ordinate system, $\alpha$ and $\beta$ would span the same quadrant since A and B are projected from the same point and have the same range. This means that for any $\beta$,
$\alpha = \dfrac{\pi}{2} - \beta$, which is indicative of their confinement to a quadrant.
$\Rightarrow \alpha + \beta = \dfrac{\pi}{2}$.
This is true since we got $\alpha=\beta$ before, which implies that
$\alpha = \dfrac{\pi}{4} = \beta \Rightarrow \alpha +\beta = \dfrac{\pi}{4} + \dfrac{\pi}{4} = \dfrac{\pi}{2}$.
Therefore, option A. $\alpha+\beta = \dfrac{\pi}{2}$ is true.
Let the vertical height reached by
A be $h_1 = \dfrac{u^2\;sin^2\alpha}{2g}$ and B be $h_2 = \dfrac{u^2\;sin^2\beta}{2g}$
Multiplying the two and taking them under root gives us:
$\sqrt{h_1h_2} = \sqrt{\dfrac{u^2\;sin^2\alpha}{2g} \times \dfrac{u^2\;sin^2\beta}{2g}}= \dfrac{u^2\;sin\alpha \;sin\beta}{2g}$
Multiply and divide the LHS by 2 and using $\beta = \dfrac{\pi}{2}-\alpha$
$\sqrt{h_1h_2} =\dfrac{u^2\;2sin\alpha\; sin\beta}{4g} = \dfrac{u^2\; 2sin\alpha \;sin\left(\dfrac{\pi}{2}-\alpha\right)}{4g} = \dfrac{u^2 \;2sin\alpha\; cos\alpha}{4g} = \dfrac{u^2\;sin2\alpha}{4g}$
$\Rightarrow 4\sqrt{h_1h_2} = \dfrac{u^2\;sin2\alpha}{g} = R$
Therefore, option B. $R =4\sqrt{h_1h_2}$ is also correct
Let the time of flight for
A be $t_1 = \dfrac{2u\;sin\alpha}{g} $ and B be $t_2 = \dfrac{2u\;sin\beta}{g}$
Dividing the two equations we get:
$\dfrac{t_1}{t_2} = \dfrac{\left(\dfrac{2u\;sin\alpha}{g} \right)}{\left(\dfrac{2u\;sin\beta}{g} \right)} = \dfrac{2u\;sin\alpha}{g} . \dfrac{g}{2u\;sin\beta} = \dfrac{sin\alpha}{sin\beta} = \dfrac{sin\alpha}{ sin\left(\dfrac{\pi}{2}-\alpha\right)} = \dfrac{sin\alpha}{cos\alpha} = tan\alpha$
Therefore, option C. $\dfrac{t_1}{t_2} = tan\alpha$ is also correct.
Let us divide the height attained by the projectiles under root.
$\sqrt{\dfrac{h_1}{h_2}} = \sqrt{\dfrac{u^2\;sin^2\alpha}{2g} . \dfrac{2g}{u^2\;sin^2\beta}} = \sqrt{\dfrac{sin^2\alpha}{sin^2\beta}} = \dfrac{sin\alpha}{sin\beta} = \dfrac{sin\alpha}{ sin\left(\dfrac{\pi}{2}-\alpha\right)} = \dfrac{sin\alpha}{cos\alpha} = tan\alpha$
Therefore, option D. $tan\alpha = \sqrt{\dfrac{h_1}{h_2}} $ is also correct.

Thus, all the options are the correct choices.

Note:
Remember to always keep in mind the cartesian visualization of projectile motion.

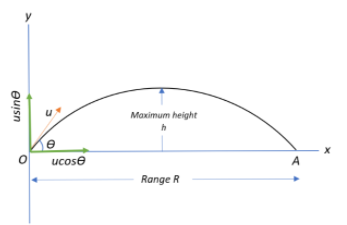
This ensures a geometrical accuracy of your evaluation by considering only those directional components necessary and helps in deducing the action and direction of velocity and gravity at each point of the trajectory. You can use this diagram to derive equations for the horizontal range, vertical height and times of flight but it is always helpful to remember them at hand.