Question

Two particles of masses m and 2m are connected by a massless string of length 3 meter and the whole system is rotating about their centre of mass with angular speed $\omega$. The kinetic energy of the system is:
A.$m\omega^2$
B.$\dfrac{1}{2}m\omega^2$
C.$6m\omega^2$
D.$3m\omega^2$

Answer 1

Hint: We are given that the system rotates about its centre of mass. In such a case, determine the position on the centre of mass of this system about the line joining the two mass particles. Then determine the distance to the centre of mass from each mass. To this end, calculate the kinetic energy of the system which will be the sum of the kinetic energy of the individual masses.
Formula Used:
Position of centre of mass $x_{cm} = \dfrac{m_1x_1+m_2x_2}{m_1+m_2}$
Kinetic energy $KE=\dfrac{1}{2}I\omega^2$
Moment of inertia $I = mr^2$

Complete answer:
We have two particles of masses $m_1 =m$ and $m_2=2m$ connected by a massless string of length $l = 3\;m$.
The whole system rotates about an axis passing through its centre of mass as shown in the figure, with an angular speed $\omega$.

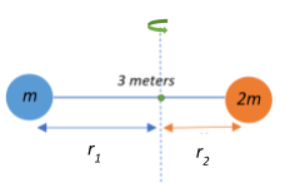
Let us begin by determining the position of the centre of mass of the system.
Let the centre of mass be located at $x_{cm}$ for the total mass of the system, and let this be located at a distance of $r_1$ from m and $r_2$ from 2m. The sum of moments will be the same for both cases.
$(m_1+m_2)x_{cm} = m_1r_1+m_2r_2$
Assuming that the centre of mass is at m, i.e., $r_1=0$ for m and $r_2=3$ for 2m, the position of the centre of mass for the system is given by:
$x_{cm} = \dfrac{m_1r_1+m_2r_2}{m_1+m_2} = \dfrac{m\times 0 +2m\times 3 }{m+2m} = \dfrac{6m}{3m} = 2\;metres$ from m.
Therefore, the distance of the centre of mass from m and 2m about which the axis of rotation is located is given as:
$\Rightarrow r_1 = 2\;metres$ and $r_2 =3-2=1\;metres$ respectively.
Now, the kinetic energy of a rotating system is directly proportional to the moment of inertia and the square of the angular velocity of the system, i.e.,
$KE = \dfrac{1}{2}I\omega^2$
Now, the moment of inertia for any system whose axis of rotation passes through its centre of mass is given as $I = \Sigma mr^2$, where m is the effective mass of the system and r is the distance of the axis of rotation from the bulk of the system where the mass is concentrated. Therefore, the kinetic energy expression for our system becomes:
$KE=\dfrac{1}{2}(m_1r_1^2+m_2r_2^2)\omega^2 = \dfrac{1}{2}(m \times 2^2 + 2m \times 1^2)\omega^2 = \dfrac{1}{2}(4m+2m)\omega^2$
$\Rightarrow KE = \dfrac{1}{2} \times 6m \times \omega^2 = 3m\omega^2$

Therefore, the correct choice would be D. $3m\omega^2$

Note:
It is important to understand the collective behaviour of components constituting a system and the factors that get influenced under their non-individualistic behaviour. We add up the moments of inertia of each mass signifying that the system now behaves as if the entire mass of the system is clumped at its centre of mass. This also influences the system’s rotatory motion which is why we have a superposed final angular speed with which the system rotates in contrast to the rotation of the individual masses, if there previously was any.
Also, always pay attention to the mentioned axis of rotation, since the expression for the moment of inertia for the same object will differ if it has a different axis of rotation.