Question

Two particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at a constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is:
A.$\dfrac{q}{2m}$
B.$\dfrac{q}{m}$
C.$\dfrac{2q}{m}$
D.$\dfrac{q}{\pi m}$

Answer 1

Hint: Begin by finding the current produced due to the rotation of charges. Recall that time can be expressed as the ratio of angular displacement to angular speed. Using the fact that the magnetic moment depends on the current sweeping through a cross-sectional area, determine an expression for the same. Then, determine the moment of inertia of the system due to the rotation of the two masses about an axis perpendicular to the centre of the rod connecting them. The angular momentum is nothing but the inertial moment due to the angular motion of the system. Arrive at an expression for the same, divide the two resultant expressions and obtain the appropriate ratio.
Formula Used:
Magnetic moment $M = i_{net}A$
Angular momentum $L = I\omega$

Complete answer:
Let us begin by first defining and understanding the terms magnetic moment and angular momentum in the context of the given system.
We are given a system consisting of two particles each of identical mass m and charge q. They are connected across the ends of a rigid rod of length 2R. The rod is rotated at a constant angular speed, say $\omega$, with the axis of rotation passing through the centre of the rod at a distance $R$ from each mass.

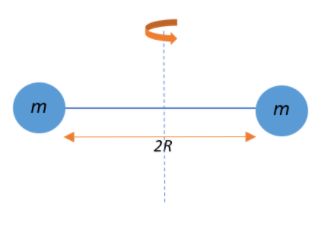
Now, magnetic moment generally determines the potential orientation of an object through a magnetic field and the magnetic strength with which it holds the position or oscillates about it. The rotation of the rod causes the charges to rotate in a circular path of radius R. Thus, each of the charges travel through an angular distance of $2\pi\;radians$ upon one rotation, say, in time t. This non-static state of a charge produces a current i by virtue of its motion. We know that current defines the rate at which a charge travels through a given (here, circular) path, i.e.,
$i =\dfrac{q}{t}$
We know that time $t = \dfrac{angular\;distance}{angular\;speed} = \dfrac{2\pi}{\omega}$.
$\Rightarrow i = \dfrac{q}{\left(\dfrac{2\pi}{\omega}\right)} = \dfrac{q\omega}{2\pi}$
Therefore, the total current due to the rotation of both charges in a circular path will be
$i_{net} = 2 \times i = 2 \times \dfrac{q\omega}{2\pi} = \dfrac{q\omega}{\pi}$
Now, the magnetic moment of the entire system will be the total current flowing through the planar cross-sectional area bound by the path taken by the rotating charges, i.e.,
$M = i_{net}A = \dfrac{q\omega}{\pi} \times \pi R^2 = q\omega R^2$
Now, the angular momentum of a rotating body is defined as the momentum with which a body executes rotatory motion that depends on the moment of inertia and the angular speed of the system and is given as:
$L = I\omega$.
The moment of inertia for the given system due to the the two particles at the end, about a perpendicular axis of rotation passing through the centre of the rod is $I =\Sigma mR^2 = mR^2+mR^2 = 2mR^2$.
$\Rightarrow L = 2mR^2\omega$
Therefore, the ratio of the magnetic moment and the angular momentum of the system is given as:
$\dfrac{M}{L} = \dfrac{q\omega R^2}{2mR^2\omega} = \dfrac{q}{2m}$

Therefore, the correct choice would be A. $\dfrac{q}{2m}$

Note:
Do not get confused between moment and momentum. The moment of any physical quantity is the product of the quantity and its perpendicular distance from the origin of its predefined coordinate system. Moment is usually the consequence of a force and the distance perpendicular to the force, whereas momentum is a result of the motion of the object. Moment defines the quantity of the force component whereas momentum defines the quantity of motion. For example, the moment of linear momentum is angular momentum, the moment of a charge is the electric dipole moment, as we’ve seen in the problem above.