Question

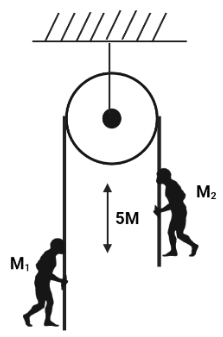
Two men of masses ${m_1}$ and ${m_2}$ hold on the opposite ends of a rope passing over a frictionless pulley. The man ${m_1}$ climbs up the pore with an acceleration of $1.2\,m{\sec ^{ - 2}}$ relative to the rope. The man ${m_2}$ climbs up the rope with an acceleration of $2\,m{\sec ^{ - 2}}$ relative to the rope. They start from rest and are initially separated by 5m. (Given ${m_1} = 40\,Kg$ and ${m_2} = 60\,Kg$).

A. Tension in the rope is $555.68\,N$
B. Tension in the rope is 556.8 N
C. Time after which they will be at the same horizontal level is 1.47 sec.
D. Time after which they will be at the same horizontal level is 2.94 sec.

Answer 1

Hint:We sketch the point of interest, all forces acting on it, and resolve all force vectors into x– and y–components to create a free-body diagram. Every object in the problem requires a separate free-body diagram.

Complete step by step answer:
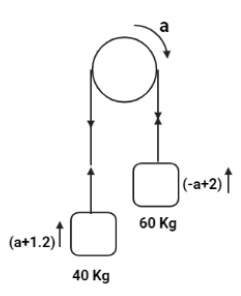
Let us consider that the acceleration of rope is $a$ which rotates in clockwise direction. Then the acceleration of ${m_1}$ will be $(a + 1.2)$ and the acceleration of ${m_2}$ will be $( - a + 2)$. So, the final diagram is as follows:

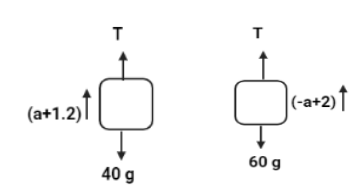
Now, let us make a free body diagram for the two masses.

Calculating the net force we will get two equations.
For the first mass:
$T - 40g = 40(a + 1.2) \\
\Rightarrow T - 40(10) = 40(a + 1.2) \\
\Rightarrow T - 400 = 40a + 48 \\
\Rightarrow T = 40a + 448 \\ $
For the second mass:
$T - 60g = 60( - a + 2) \\
\Rightarrow T - 60(10) = 60( - a + 2) \\
\Rightarrow T - 600 = - 60a + 120 \\
\Rightarrow T = - 60a + 720 \\ $
Comapring the above two equations we get,
$40a + 448 = - 60a + 720 \\
\Rightarrow 100a = 272 \\
\Rightarrow a = 2.72m.{\sec ^{ - 2}} \\ $
Now, lets calculate the value of Tension using this value
$T = - 60a + 720 \\
\Rightarrow T = - 60(2.72) + 720 \\
\Rightarrow T = - 163.2 + 720 \\
\Rightarrow T = 556.8N \\ $
Hence, option (B) is correct as Tension in the rope is 556.8N.
Now, we will calculate the individual acceleration of each mass
${a_1} = a + 1.2 \\
\Rightarrow {a_1} = 2.72 + 1.2 \\
\Rightarrow {a_1} = 3.92\,m.{\sec ^{ - 2}} \\ $
Similarly,
${a_2} = - a + 2 \\
\Rightarrow {a_2} = - 2.72 + 2 \\
\Rightarrow {a_2} = - 0.72m.{\sec ^{ - 2}} \\ $
Now we should calculate the time when both the masses will be in the same horizontal height. Hence, we will use the following formula,
$s = ut + \dfrac{1}{2}a{t^2} \\
\Rightarrow 5 = 0(t) + \dfrac{1}{2}(2.72){t^2} \\
\Rightarrow 10 = 2.72{t^2} \\
\Rightarrow {t^2} = 3.67 \\
\therefore t = 1.48\sec $
Therefore, Option (c) is also correct as time after which they will be at the same horizontal level is 1.47 sec.

Hence, we conclude that option B and option C are the correct answer.

Note:Objects are not often subjected to four powers. The number of forces represented by a free-body diagram can be one, two, or three in some situations. The number of forces that must be drawn in a free-body diagram is not a hard and quick guideline. Drawing free-body diagrams has only one rule: represent all of the forces that occur with that entity in the specified case.