Question

Two long straight wires are set parallel to each other at separation r and each carries a current i in the same direction. The strength of the magnetic field at any point midway between the two wires is:
A.$\dfrac{\mu_0i}{\pi r}$
B.$\dfrac{2\mu_0i}{\pi r}$
C.$\dfrac{\mu_0i}{2\pi r}$
D.Zero

Answer 1

Hint: Recall that any current carrying conductor produces a magnetic field around it. Use the right hand thumb rule to determine the direction of the magnetic field produced by each wire at a point midway between the two wires. Account for the difference in signs on the magnetic field direction if any, and consequently determine the resultant strength of the magnetic field at that point.
Formula Used:
Magnetic field strength $B = \dfrac{\mu_0\vec{i}}{2\pi r}$

Complete answer:
We know that stationary charges produce an electric field which is proportional to the magnitude of the charge. But current pertains to the rate of flow of charge. So, similarly, moving charges produce magnetic fields which are proportional to the current. We can thus say that a current carrying conductor produces a magnetic field around it, and is attributed to the movement of electrons between atomic orbitals in the material of a conductor.
The magnetic field produced encircles the conductor and lies in a plane perpendicular to that of the conductor. Any reversal in the current flow reverses the direction of the magnetic field. This is given by the right hand thumb rule which states that if the thumb points in the direction of current flow, then the curling of the rest of the fingers indicate the direction of the magnetic field. The strength of this magnetic field is proportional to the current flowing through the conductor and gets weaker with distance from the wire, i.e.,
$\vec{B} \propto \dfrac{i}{2\pi r} \Rightarrow \vec{B} = \dfrac{\mu_0i}{2\pi r}$, where $\mu_0$ is the proportionality constant which is the magnetic permeability of free space.
Now, let us dive into the context of our question.
We have two current carrying conductors that carry the same magnitude and direction of current i and are a distance r apart.
Let us consider a point midway between the two wires as shown in the diagram.

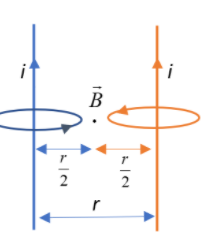
This point will be at a distance $\dfrac{r}{2}$ from each wire.
The strength of the magnetic field at this point will be the additive sum of the magnetic fields produced due to the current carrying wires. Since both the wires carry the same current and are at the same distance from the point, the magnitude of the magnetic field produced by these two wires will be the same, i.e.,
$|\vec{B_1}| = |\vec{B_2}| = \dfrac{\mu_0i}{2\pi \left(\dfrac{r}{2}\right)} = \dfrac{\mu_0i}{\pi r}$
Let us now determine the direction of these magnetic fields. From the right hand thumb rule, we see that the magnetic field due to the left wire at the given point is directed into the plane of the paper whereas the magnetic field due to the right wire at the given point is pointed away from the plane of the paper towards us. The two magnetic fields at the point act in directions opposite to each other, i.e.,
$\vec{B_1} = -\vec{B_2}$
$\Rightarrow \vec{B_1} = \dfrac{\mu_0i}{\pi r}$ and $\vec{B_2} = -\dfrac{\mu_0i}{\pi r}$
The resulting magnetic field acting at this point will be the sum of the magnetic field due to each wire, i.e.,
$\vec{B} = \vec{B_1} +\vec{B_2} = \dfrac{\mu_0i}{\pi r} - \dfrac{\mu_0i}{\pi r} = 0$

Therefore, the correct choice would be D. Zero

Note:
Do not get confused between the right hand rule and the right hand thumb rule.
The right hand rule involves using three fingers aligned in perpendicular directions to each other, where the magnetic force (indicated by thumb), the moving charge or current (indicated by index finger) and the magnetic field direction (indicated by the middle finger) can be determined.
The right hand “thumb” rule involves a closed fist, with the upright thumb pointing in the direction of current flow and the fist representing the direction of the magnetic field lines.