Question

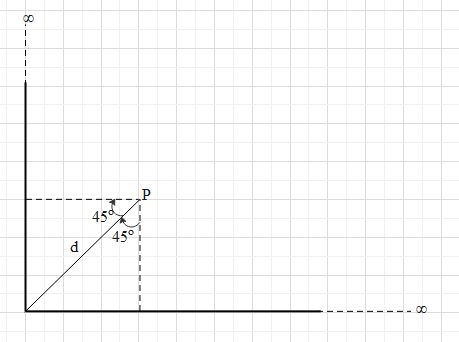
Two infinitely long uniformly charged rods are joined as shown in the figure. The linear charge density on the rod is $\lambda =\dfrac{Q}{L}$, Q is the total charge on each rod and L is the length of each rod. Find the electric field in vector form at point P due to the two rods.

Answer 1

Hint: Understand how uniformly charged rod of some length produces an electric field at point P that is at a perpendicular distance d from the rod. Apply this formula for both the given rods and calculate the net electric field at point P.

Formula used:
${{E}_{x}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
${{E}_{y}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \cos {{\theta }_{1}}-\cos {{\theta }_{2}} \right)$

Complete step by step answer:
Let them understand the electric field due to a charged finite rod.
Suppose a uniformly charged rod of linear charge density $\lambda $ is placed vertically as shown. Then the electric field at a point P that is at a perpendicular distance d from the rod is given as:
${{E}_{x}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
And
${{E}_{y}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \cos {{\theta }_{1}}-\cos {{\theta }_{2}} \right)$

Here, ${{E}_{x}}$ is the horizontal component of the electric field and ${{E}_{y}}$ is the vertical component of the electric field.
${{\theta }_{1}}$ and ${{\theta }_{2}}$ are the angles as shown in the figure.
Therefore, in vector form the electric field will be $E=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)\widehat{i}+\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \cos {{\theta }_{1}}-\cos {{\theta }_{2}} \right)\widehat{j}$
Let us now find the net electric field to the two rods as per arrangements shown in the figure of the question.
Let us find the electric field (${{E}_{1}}$) due to the vertical rod. For this rod, the perpendicular distance of the point P is $d\cos 45=\dfrac{d}{\sqrt{2}}$.

Since the rod is going up till infinity, ${{\theta }_{1}}\approx {{90}^{\circ }}$.
From the figure, ${{\theta }_{2}}={{45}^{\circ }}$.
Therefore,
$\Rightarrow {{E}_{1}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}\dfrac{d}{\sqrt{2}}}\left( \sin 90+\sin 45 \right)\widehat{i}+\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}\dfrac{d}{\sqrt{2}}}\left( \cos 90-\cos 45 \right)\widehat{j}$
$\Rightarrow {{E}_{1}}=\dfrac{\sqrt{2}\lambda }{4\pi {{\varepsilon }_{0}}d}\left( 1+\dfrac{1}{\sqrt{2}} \right)\widehat{i}+\dfrac{\sqrt{2}\lambda }{4\pi {{\varepsilon }_{0}}d}\left( 0-\dfrac{1}{\sqrt{2}} \right)\widehat{j}$
$\Rightarrow {{E}_{1}}=\dfrac{\left( \sqrt{2}+1 \right)\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{i}-\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{j}$
Let us find the electric field (${{E}_{2}}$) due to the horizontal rod.

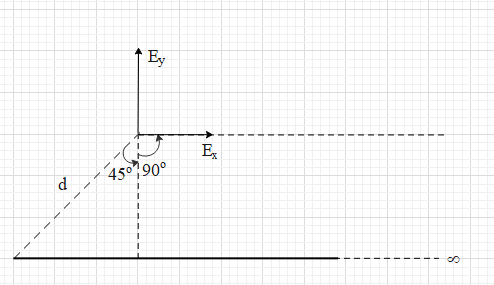
Here, the perpendicular distance is $d\cos 45=\dfrac{d}{\sqrt{2}}$.
${{\theta }_{1}}\approx {{90}^{\circ }}$ and ${{\theta }_{2}}={{45}^{\circ }}$.
However, in this case the horizontal component will be ${{E}_{x}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \cos {{\theta }_{1}}-\cos {{\theta }_{2}} \right)$.
The vertical component will be ${{E}_{y}}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$.
Since the data is same, we get that
${{E}_{2}}=\dfrac{-\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{i}+\dfrac{\left( \sqrt{2}+1 \right)\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{j}$
The net electric field at point P is $\overrightarrow{E}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{1}}}$.
$\Rightarrow \overrightarrow{E}=\dfrac{\left( \sqrt{2}+1 \right)\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{i}-\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{j}+\dfrac{-\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{i}+\dfrac{\left( \sqrt{2}+1 \right)\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{j}$
$\Rightarrow \overrightarrow{E}=\dfrac{\sqrt{2}\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{i}+\dfrac{\sqrt{2}\lambda }{4\pi {{\varepsilon }_{0}}d}\widehat{j}$
$\Rightarrow \overrightarrow{E}=\dfrac{\sqrt{2}\lambda }{4\pi {{\varepsilon }_{0}}d}\left( \widehat{i}+\widehat{j} \right)$
It is given that $\lambda =\dfrac{Q}{L}$.
$\Rightarrow \overrightarrow{E}=\dfrac{\sqrt{2}Q}{4\pi {{\varepsilon }_{0}}dL}\left( \widehat{i}+\widehat{j} \right)$
The above expression is the net electric field in vertical form at point P.

Note:
Note that the formula for the horizontal and vertical components of the electric due to a vertical rod is applicable only for a vertical rod. When the rod rotates by 90 degrees, the formula will change.