Question

Two inclined planes OA and OB having inclination ${{30}^{\circ }}$ and ${{60}^{\circ }}$ respectively with the horizontal, intersect each other at O, as shown in the figure. A particle is projected from point P with velocity $u=10\sqrt{3}m{{s}^{-1}}$ along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q, calculate the time to flight.
A.$4s$
B.$3s$
C.$2s$
D.$5s$

Answer 1

Hint:In this problem, we are given a new system of XY-plane and we shall not follow the regular notion of x-axis in the horizontal direction and y-axis in the vertical direction. Hence, we shall analyze the components of velocity as well as acceleration vectors according to the inclination of the plane of the particle that has been projected. Subsequently, we apply the equations of motion to find the time of flight of particles.

Complete answer:
We see that the initial velocity of the particle is perpendicular to the y-axis. Thus, the particle has velocity only in x-direction and the y-component of initial velocity is zero.
Thus, the x-component of initial velocity, ${{u}_{x}}=10\sqrt{3}m{{s}^{-1}}$ (given in question)
And the y-component of initial velocity, ${{u}_{y}}=0m{{s}^{-1}}$
However, the acceleration due to gravity acting on the particle due to the force of gravity is acting in the downward direction irrespective of the new system of XY-plane given to us. Therefore, we shall the x-component and y-component of acceleration.

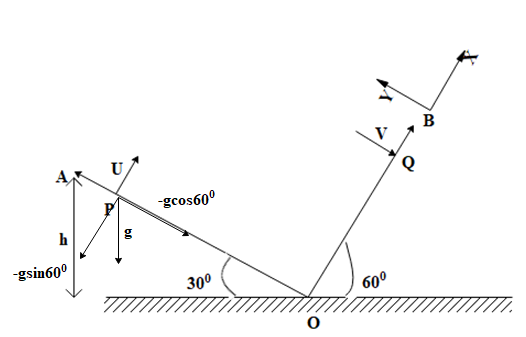
The x-component of acceleration, ${{a}_{x}}=-g\cos {{30}^{\circ }}$
The y-component of acceleration, ${{a}_{y}}=-g\cos {{60}^{\circ }}$
Let us take acceleration due to gravity, $g=10m{{s}^{-2}}$ and we know that $\cos {{60}^{\circ }}=\dfrac{1}{2}$ and $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$ , therefore, we get
${{a}_{x}}=-10.\dfrac{\sqrt{3}}{2}=-5\sqrt{3}m{{s}^{-2}}$ and ${{a}_{y}}=-10.\dfrac{1}{2}=-5m{{s}^{-2}}$
Now, we shall use the first equation of motion in the x-direction of motion,
${{v}_{x}}={{u}_{x}}+{{a}_{x}}t$
Where,
${{v}_{x}}=$ x-component of final velocity $=0m{{s}^{-1}}$ because the final velocity of particle is only in y-direction
${{u}_{x}}=$ x-component of initial velocity $=10\sqrt{3}m{{s}^{-1}}$ (given)
${{a}_{x}}=$ x-component of acceleration $=-5\sqrt{3}m{{s}^{-2}}$
$t=$ time taken
We get, $0=10\sqrt{3}+\left( -5\sqrt{3} \right)t$
$\begin{align}
  & \Rightarrow 5\sqrt{3}t=10\sqrt{3} \\
 & \Rightarrow t=\dfrac{10\sqrt{3}}{5\sqrt{3}} \\
 & \Rightarrow t=2s \\
\end{align}$
Therefore, the time of flight of particles is 2 seconds.

Hence, the correct option is (C) $2s$.

Note:
One of the most common mistakes made by solving such problems involving different and new defined systems of coordinates is that the components of various vectors required are not resolved properly. The angles are not properly understood and we end up getting incorrect values of the quantities we are given to find in the question. Hence, we must be more careful in this.