Question

Two finite sets have m and n elements. The number of subsets of the first set is 112 more than of the second set. The values of m and n respectively are
A. 4, 7
B. 7, 4
C. 4, 4
D. 7, 7

Answer 1

Hint: The number of subsets of m, n elements will be ${{2}^{m}},{{2}^{n}}$ respectively so it can be written as ${{2}^{m}}-{{2}^{n}}=112$. After that factorize 112 to separate factors of 2 and then equate the equation to get the desired result.

Complete step-by-step solution:
We are given two finite sets with m and n elements. If the number of elements is ‘l’ then the number of subsets are ${{2}^{l}}$.
Just for an example consider a set like {1,2,3} then its subsets are {1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},{}.
Hence the numbers of elements were 3 and its number of subsets is ${{2}^{3}}=8$ which is given.
So if the elements of a set are m and n so the number of subsets are ${{2}^{m}}$ and ${{2}^{n}}$ respectively.
In the question we are given that the numbers of subsets with m elements are 112 more than the number of subsets with n elements.
So we can write as,
${{2}^{m}}-{{2}^{n}}=112\ldots \ldots (1)$
We can take ${{2}^{n}}$ common in left hand side of (1) we get,
${{2}^{n}}({{2}^{m-n}}-1)=112\ldots \ldots (2)$
Now let’s analyse the left hand side of (1) we can see that it’s a product of an even and an odd number. The even number will have only 2 as its prime factor so we can factorize 112 as,

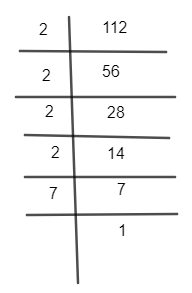
So 112 can be written as ${{2}^{4}}\times 7.$
Now we will substitute it in equation (2) so we get,
${{2}^{n}}\left( {{2}^{m-n}}-1 \right)={{2}^{4}}\times 7\ldots \ldots (3)$
No, $\left( {{2}^{m-n}}-1 \right)$can never be equal to ${{2}^{4}}$ as one is odd and other is even.
So,
${{2}^{n}}={{2}^{4}}$
Now we can apply law which is when bases are equal exponents are the same.
So the value of n=4.
Now we will put n=4 in equation (3) we get,
${{2}^{4}}\left( {{2}^{m-4}}-1 \right)={{2}^{4}}\times 7$
which can be further represented as,
${{2}^{m-4}}-1=7\ldots \ldots (4)$
Now adding 1 in both the sides of equation (4) we get,
${{2}^{m-4}}=8$
Now we can represent 8 as \[{{2}^{3}}\] to make the bases equal so it can be further written as,
${{2}^{m-4}}={{2}^{3}}$
Applying law of indices which bases are same exponents are equal we get,
m-4 = 3
So, the value of m=7.
Hence the answer is B.

Note: In this question one can tell answer without even solving it as we know that the subsets of m elements are greater than that of n elements then m and n cannot be equal so option C, D cancels out and m should always be greater than n so option A. also cancels B. is the answer.