Question

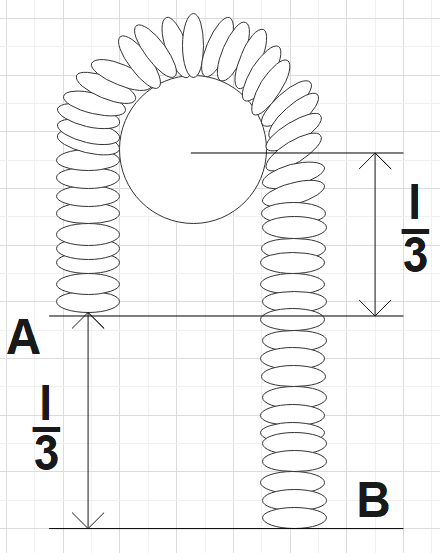
Two ends A and B of a smooth chain of mass m and length l are situated as shown in the figure. If an external agent pulls A till it comes to the same level of B. Find the work done by the external agent to make the chain on the same level.

Answer 1

Hint: As a very first step, one could read the question well and hence note down the important points from the question. Apply your logic to find the change to be made to make the ends at the same level. Then find that potential energy is changed in this process and hence find the work done.
Formula used:
Potential energy,
$P.E=mgh$

Complete step-by-step solution:
In the question we are given a chain with ends A and B of length l and mass m. It is also said that an external agent pulls the end A and thereby making both ends to be at the same level. We are supposed to find the work done by the external agent so as to make the ends at the same level.
Logically we know that if half of the length $\dfrac{l}{3}$(which is the difference between the two end levels) is added to the A end we could make the ends at the same level.
That is, we could assume that,
A length $\dfrac{l}{6}$is cut from the B end and is added to the A end thus making both ends at the same level. The equivalent mass of this length of chain would be$\dfrac{m}{6}$.
Now, we could find the change potential energy to be,
$\Delta PE=\dfrac{m}{6}g\dfrac{l}{6}-0=\dfrac{mgl}{36}$
Now, this would be the work done by the external agent in the given case.
$\therefore W=\dfrac{mgl}{36}$

Note: We have assumed the chain to be uniform and hence concluded that the mass would be proportional to the length. Basically, this question is answered with logical thinking. Also, one should also know that work is done to change the level of the ends of the chain which would imply that there is a change in potential energy.