
Two different dice are tossed together. Find the probability of getting a doublet.
Answer
606.9k+ views
Hint: A dice has the shape of a cube having one number from 1, 2, 3, 4, 5 and 6 printed on each of the faces of the cube. Getting a doublet means both the numbers on the dice are the same. A dice can have one of the six outcomes from 1, 2, 3, 4, 5 and 6.
Complete step-by-step answer:
We have been given that two dice have been tossed. Since the number of outcomes on a single dice is 6, therefore the total number of outcomes when two dices are tossed will be \[6\times 6=36\]. This is called sample space or the total number of events that may occur. The different outcomes are shown in the table below:
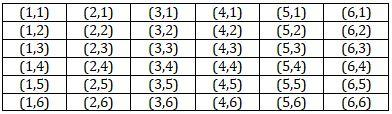
Observing the table carefully, we come to the conclusion that there are six doublets (1,1), (2,2), (3,3), (4,4), (5,5) and (6,6). These are the favourable outcomes. Hence, the number of favourable outcomes is 6.
Therefore we have sample space, denoted by \[n\left( s \right)=36\]. And number of favourable outcomes, denoted by \[n\left( e \right)=6\].
We know that the probability of an event, denoted by \[\text{P}\left( e \right)\] is given by:
$\text{P}(e)=\dfrac{n(e)}{n(s)}........................................(1)$
Here, we have \[n\left( s \right)=36\] and $n(e)=6$.
Substituting these values in equation \[\left( 1 \right)\], we get;
$\text{P}(e)=\dfrac{6}{36}=\dfrac{1}{6}.$
Note: One should properly know the concept of probability and its formula to solve questions. We should understand the meaning of terms like doublet, triplet and likewise. If there would have been three dice, then the total number of outcomes would have been $n(s)=6\times 6\times 6=216$. For $n$ number of dices, the total number of outcomes will be $n(s)={{6}^{n}}$.
Complete step-by-step answer:
We have been given that two dice have been tossed. Since the number of outcomes on a single dice is 6, therefore the total number of outcomes when two dices are tossed will be \[6\times 6=36\]. This is called sample space or the total number of events that may occur. The different outcomes are shown in the table below:

Observing the table carefully, we come to the conclusion that there are six doublets (1,1), (2,2), (3,3), (4,4), (5,5) and (6,6). These are the favourable outcomes. Hence, the number of favourable outcomes is 6.
Therefore we have sample space, denoted by \[n\left( s \right)=36\]. And number of favourable outcomes, denoted by \[n\left( e \right)=6\].
We know that the probability of an event, denoted by \[\text{P}\left( e \right)\] is given by:
$\text{P}(e)=\dfrac{n(e)}{n(s)}........................................(1)$
Here, we have \[n\left( s \right)=36\] and $n(e)=6$.
Substituting these values in equation \[\left( 1 \right)\], we get;
$\text{P}(e)=\dfrac{6}{36}=\dfrac{1}{6}.$
Note: One should properly know the concept of probability and its formula to solve questions. We should understand the meaning of terms like doublet, triplet and likewise. If there would have been three dice, then the total number of outcomes would have been $n(s)=6\times 6\times 6=216$. For $n$ number of dices, the total number of outcomes will be $n(s)={{6}^{n}}$.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




