Question

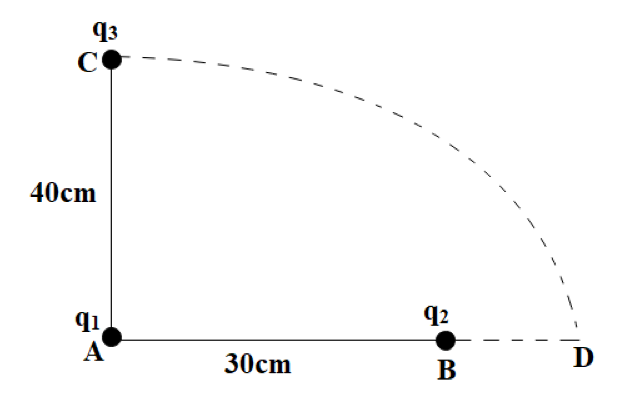
Two charges ${{q}_{1}}$ and ${{q}_{2}}$ are placed 30cm apart, as shown in figure. A third charge ${{q}_{3}}$ is moved along the arc of a circle of radius 40cm from C to D. the change in the potential energy of the system is $\dfrac{{{q}_{3}}}{4\pi {{\varepsilon }_{0}}}k$ , where $k$ is
A.$8{{q}_{1}}$
B.$6{{q}_{1}}$
C.$8{{q}_{2}}$
D.$6{{q}_{2}}$

Answer 1

Hint:We are given two charges and a third charge is entering their in space. These already present charges had some potential energy due to each other and third charge at point C. This will be considered as the initial potential energy of the system. When a third charge is introduced, they develop more potential energy due to it. This sums up as the final potential energy. We will subtract the initial and final potential energies to get the change in potential energy.

Complete answer:
The potential energy, $U$ of any charged body is given as:
$U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}.\dfrac{{{q}_{1}}{{q}_{2}}}{r}$
Where,
${{q}_{1}}=$ charge on first body
${{q}_{2}}=$ charge on second body
$r=$ distance between the two charges
We have $AB=30cm,AC=40cm$, thus by Pythagorean triplets, BC is given as:
$\begin{align}
  & BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}} \\
 & \Rightarrow BC=\sqrt{{{30}^{2}}+{{40}^{2}}} \\
 & \Rightarrow BC=\sqrt{900+1600} \\
 & \Rightarrow BC=\sqrt{2500} \\
\end{align}$
$\therefore BC=50cm$
Also,
 $\begin{align}
  & BD=AD-AB \\
 & \Rightarrow BD=40-30 \\
 & \Rightarrow BD=10cm \\
\end{align}$
For a discrete system of charges, the potential energy is expressed as the sum of all potential energies of the system.
$U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{{{r}_{12}}}+\dfrac{{{q}_{2}}{{q}_{3}}}{{{r}_{23}}}+\dfrac{{{q}_{1}}{{q}_{3}}}{{{r}_{13}}} \right]$
For the initial potential energy when ${{q}_{3}}$ is at point C,
${{r}_{12}}=AB=30cm=0.3m$, ${{r}_{23}}=BC=50cm=0.5m$, ${{r}_{13}}=AC=40cm=0.4m$
The potential energy is calculated as:
${{U}_{i}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{AB}+\dfrac{{{q}_{2}}{{q}_{3}}}{BC}+\dfrac{{{q}_{1}}{{q}_{3}}}{AC} \right]$
$\Rightarrow {{U}_{i}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{0.3}+\dfrac{{{q}_{2}}{{q}_{3}}}{0.5}+\dfrac{{{q}_{1}}{{q}_{3}}}{0.4} \right]$ ………………… equation (1)
For the final potential energy when ${{q}_{3}}$ is at point D,
${{r}_{12}}=AB=30cm=0.3m$, ${{r}_{23}}=BD=10cm=0.1m$, ${{r}_{13}}=AD=40cm=0.4m$
The potential energy is calculated as:
${{U}_{f}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{AB}+\dfrac{{{q}_{2}}{{q}_{3}}}{BD}+\dfrac{{{q}_{1}}{{q}_{3}}}{AD} \right]$
$\Rightarrow {{U}_{f}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{0.3}+\dfrac{{{q}_{2}}{{q}_{3}}}{0.1}+\dfrac{{{q}_{1}}{{q}_{3}}}{0.4} \right]$ ………………… equation (2)
Change in potential energy= final potential energy – initial potential energy
$\Rightarrow \Delta U={{U}_{f}}-{{U}_{i}}$
From equation (1) and (2),
$\Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{0.3}+\dfrac{{{q}_{2}}{{q}_{3}}}{0.1}+\dfrac{{{q}_{1}}{{q}_{3}}}{0.4} \right]-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{0.3}+\dfrac{{{q}_{2}}{{q}_{3}}}{0.5}+\dfrac{{{q}_{1}}{{q}_{3}}}{0.4} \right]$
Taking $\dfrac{1}{4\pi {{\varepsilon }_{0}}}$ common, we get
$\Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{{{q}_{1}}{{q}_{2}}}{0.3}+\dfrac{{{q}_{2}}{{q}_{3}}}{0.1}+\dfrac{{{q}_{1}}{{q}_{3}}}{0.4}-\dfrac{{{q}_{1}}{{q}_{2}}}{0.3}-\dfrac{{{q}_{2}}{{q}_{3}}}{0.5}-\dfrac{{{q}_{1}}{{q}_{3}}}{0.4} \right]$
$\begin{align}
  & \Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ {{q}_{2}}{{q}_{3}}\left( \dfrac{1}{0.1}-\dfrac{1}{0.5} \right) \right] \\
 & \Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ {{q}_{2}}{{q}_{3}}\left( \dfrac{0.5-0.1}{0.1\left( 0.5 \right)} \right) \right] \\
\end{align}$
$\Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ {{q}_{2}}{{q}_{3}}\dfrac{0.40}{0.05} \right]$
$\Rightarrow \Delta U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}8{{q}_{2}}{{q}_{3}}$
Therefore, the change in potential energy is equal to $\dfrac{1}{4\pi {{\varepsilon }_{0}}}8{{q}_{2}}{{q}_{3}}$.

Hence, the correct option is (C) $8{{q}_{2}}$

Note:
Every charged body has its own electric potential. However, the potential energy of any charged body is always measured with respect to some other charged body in its vicinity. This is because any charged body develops a potential energy due to interaction with another charged body near it. The potential energy of any charged body is zero if it is isolated in space.