Question

When two capillary tubes of different diameters are dipped vertically, the rise of the liquid will be given as,
A. similar in both the tubes.
B. more in tube having larger diameter.
C. less in the tube having smaller diameter.
D. more in the tube having smaller diameter.

Answer 1

Hint: The height at which the rise of the liquid in the capillary take place is calculated by the formula which tells that the ratio of the twice of the product of the tension and the cosine of the angle to the product of the density, acceleration due to gravity and the radius of the capillary tube. From this equation we will get the relation between the radius of the tube and the height of the rise of the liquid in it. This information will help you to solve this question.

Complete answer:
As we all know, the rise of the liquid column inside the capillary tube can be found using the equation given as,
$h=\dfrac{2T\cos \theta }{\rho gR}$
Where $h$ be the height of the liquid column, $T$ be the tension of the liquid, $\theta $ be the angle present there, $\rho $ be the density of the liquid, $g$ be acceleration due to gravity and $R$ be the radius of the capillary tube. In this equation, the value of acceleration due to gravity, density of the liquid and tension of the liquid are the same for both the cases as the same liquid has been used. Therefore we can write that,
$h\propto \dfrac{1}{R}$

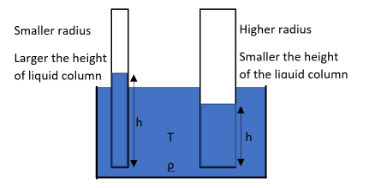
That is as the radius of the capillary tube increases, the height of the rise of the liquid column is smaller. And if the radius of the tube decreases, then the height of the rise of the liquid column will be higher.

So, the correct answer is “Option D”.

Note:
The surface tension of a liquid will cause an imbalance of intermolecular attractive forces and the cohesive forces between molecules. A molecule in the bulk liquid will feel cohesive forces with other molecules in every possible direction. A molecule at the surface of a liquid will have only resultant inward cohesive forces.