Question

Two bullets are fired with horizontal velocities of $50m{{s}^{-1}}$ and $100m{{s}^{-1}}$ from two guns at a height of $19.6m$.
a).Will both the bullets strike the ground?
b).If yes, then after how much time and which bullet will strike first?
c).What would be the path of the bullets? $\left( g=9.8m{{s}^{-2}} \right)$

Answer 1

Hint: We shall analyze the motion of the bullets due to their vertical acceleration due to gravity. Since the bullets have a horizontal component of velocity, therefore they will not be falling freely in a straight-line path due to action of gravity. Thus, we will apply equations of motion in the vertical motion to find the time taken.

Complete answer:

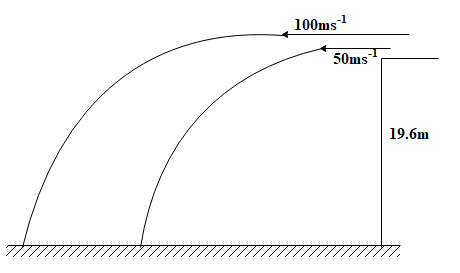
a).Initially, the bullets have only a horizontal component of velocity and the vertical component of velocity is zero. However, the bullets have an acceleration in the downward direction which makes their path semi-parabolic. Thus, both the bullets will strike the ground due to their acceleration due to gravity in the vertically downward direction.

b).Time taken in for the bullets to reach the ground is given by Newton’s second equation of motion. The equation is:
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
Where,
$s=$ displacement of body
$u=$ initial velocity of body
$t=$ time taken
$a=$ acceleration of the body
We shall apply this equation for the vertical motion of the bullets only. The vertical component of initial velocity is zero for both the bullets. Thus, $u=0$. The vertical acceleration acting on the bullets is the acceleration due to gravity. Thus, $a=g$. The vertical height from which the bullets are being fired is $19.6m$. Thus, $s=19.6m$.
Thus, we get the equation as:
$19.6=\left( 0 \right)t+\dfrac{1}{2}g{{t}^{2}}$
$\Rightarrow 19.6=\dfrac{1}{2}g{{t}^{2}}$
Given that $g=9.8m{{s}^{-2}}$,
 $\Rightarrow 19.6=\dfrac{1}{2}\left( 9.8 \right){{t}^{2}}$
$\Rightarrow {{t}^{2}}=\dfrac{19.6\left( 2 \right)}{9.8}$
$\Rightarrow {{t}^{2}}=4$
$\begin{align}
  & \Rightarrow t=\sqrt{4} \\
 & \Rightarrow t=\pm 4 \\
\end{align}$
Ignoring the negative value because time is always positive.
Therefore, both the bullets will strike the ground at the same time, that is, $2$seconds. This is because the time taken is independent of initial velocities of bullets.

c).The path followed by the bullets will be a semi-parabolic path with different range due to different horizontal velocities.

Note:
Here, we see that the time taken by the bullets to strike the ground is independent of the velocity of the bullet. It is only dependent on the vertical and acceleration which is the same for both the bullets. Hence, both bullets will strike the ground at the same time.