
Two brands of chocolates are available in packs of 24 and 15 respectively. If I need to buy an equal number of chocolates of both kinds, what is the least number of boxes of each kind I would need to buy?
A. 2 of first kind, 8 of second kind
B. 5 of first kind, 8 of second kind
C. 5 of first kind, 7 of second kind
D. 2 of first kind, 7 of second kind
Answer
608.4k+ views
Hint: By prime factorization method take the LCM of the number of chocolates of both brands. To get the least number of boxes, find LCM (24, 15) to the number of chocolate per box.
“Complete step-by-step answer:”
Given the number of chocolate of ${{1}^{st}}$ brand in one pack = 24
The number of chocolate of ${{2}^{nd}}$ brand in one pack = 15
To find the least number of boxes of each kind first we have to find the LCM of 24 and 15.
LCM by prime factorization method.
The method of prime factorization is used to “break down” or express a given number as a product of prime numbers.
The prime number will occur more than once in the prime factorization.
Where the prime number is a whole number which is greater than 1, it is only divisible by 1 and itself.
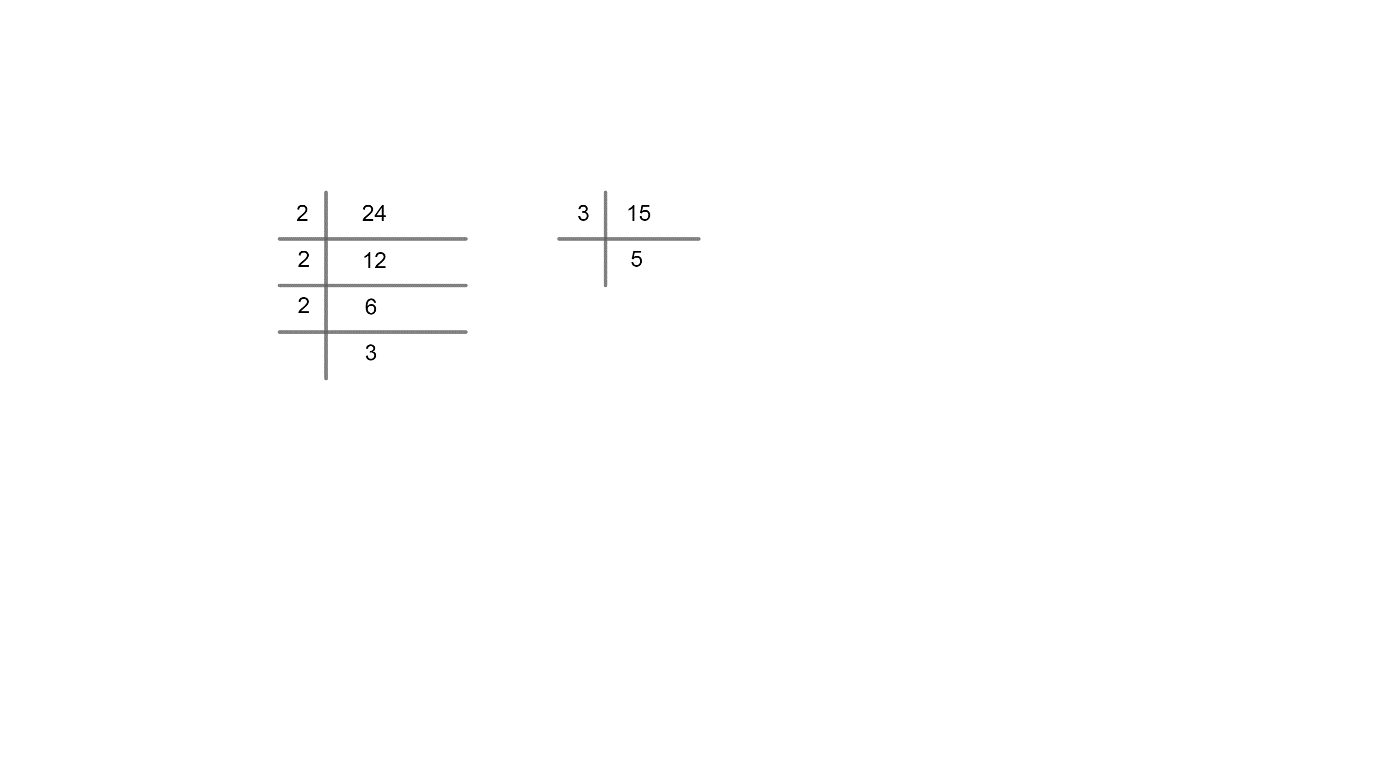
LCM of 24 $=2\times 2\times 2\times 3={{2}^{3}}\times 3$
LCM of 15 $=3\times 5$
LCM of two numbers = product of the greater power of each prime factor involved in the numbers, with highest power.
LCM of 24 \[=2\times 2\times 2\times \times 5\]
LCM of 15 $=\times 5$
$\therefore $ LCM of 24 and 15 $=2\times 2\times 2\times 3\times 5$
LCM (24, 15) = 120
Hence, the number of packet of ${{1}^{st}}$ brand $=\dfrac{\text{LCM }\left( 24,15 \right)}{\text{Number of chocolate in }{{\text{1}}^{st}}\text{ brand}}$
Number of packets in ${{2}^{nd}}$ brand $=\dfrac{\text{LCM }\left( 24,15 \right)}{\text{Number of chocolate in }{{\text{2}}^{nd}}\text{ brand}}$
$=\dfrac{120}{15}=8$
$\therefore $ 5 of first kind, 8 of second kind
Note: Another way of finding the least number of boxes of both kind,
Number of packet of ${{1}^{st}}$ brand = 24 = 3 x 8
Number of packets in ${{2}^{nd}}$ brand = 15 = 3 x 5
24 = 3 x 8
15 = 3 x 5
$\therefore $ 8 of ${{1}^{st}}$kind and 5 of ${{2}^{nd}}$kind.
“Complete step-by-step answer:”
Given the number of chocolate of ${{1}^{st}}$ brand in one pack = 24
The number of chocolate of ${{2}^{nd}}$ brand in one pack = 15
To find the least number of boxes of each kind first we have to find the LCM of 24 and 15.
LCM by prime factorization method.
The method of prime factorization is used to “break down” or express a given number as a product of prime numbers.
The prime number will occur more than once in the prime factorization.
Where the prime number is a whole number which is greater than 1, it is only divisible by 1 and itself.
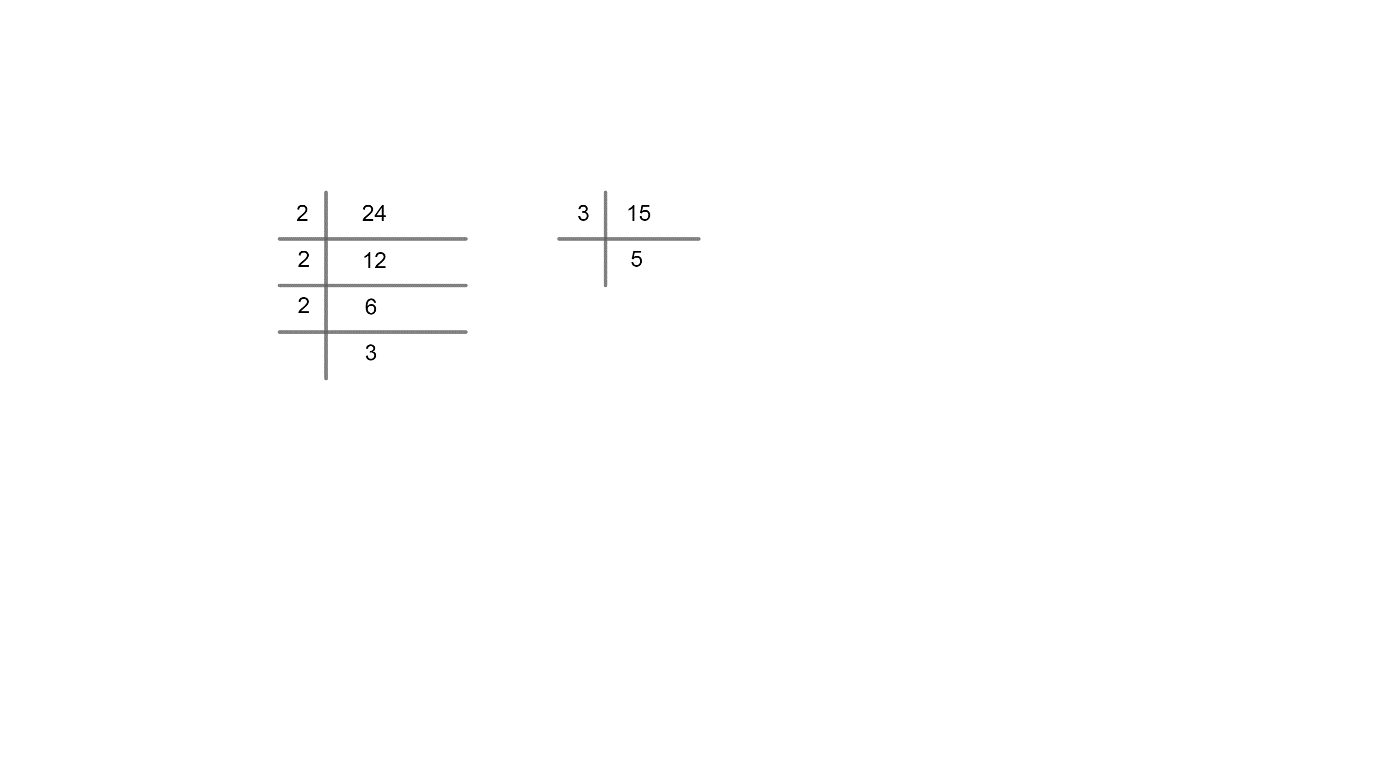
LCM of 24 $=2\times 2\times 2\times 3={{2}^{3}}\times 3$
LCM of 15 $=3\times 5$
LCM of two numbers = product of the greater power of each prime factor involved in the numbers, with highest power.
LCM of 24 \[=2\times 2\times 2\times \times 5\]
LCM of 15 $=\times 5$
$\therefore $ LCM of 24 and 15 $=2\times 2\times 2\times 3\times 5$
LCM (24, 15) = 120
Hence, the number of packet of ${{1}^{st}}$ brand $=\dfrac{\text{LCM }\left( 24,15 \right)}{\text{Number of chocolate in }{{\text{1}}^{st}}\text{ brand}}$
Number of packets in ${{2}^{nd}}$ brand $=\dfrac{\text{LCM }\left( 24,15 \right)}{\text{Number of chocolate in }{{\text{2}}^{nd}}\text{ brand}}$
$=\dfrac{120}{15}=8$
$\therefore $ 5 of first kind, 8 of second kind
Note: Another way of finding the least number of boxes of both kind,
Number of packet of ${{1}^{st}}$ brand = 24 = 3 x 8
Number of packets in ${{2}^{nd}}$ brand = 15 = 3 x 5
24 = 3 x 8
15 = 3 x 5
$\therefore $ 8 of ${{1}^{st}}$kind and 5 of ${{2}^{nd}}$kind.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




