Question

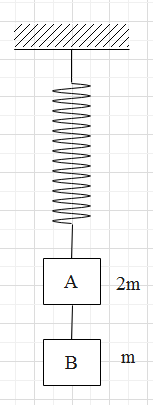
Two blocks A and B of masses 2m and m, respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitude of the acceleration of A and B immediately after the string is cut, are respectively:

\[A.\,g,\dfrac{g}{2}\]
\[B.\,\dfrac{g}{2},g\]
\[C.\,g,g\]
\[D.\,\dfrac{g}{2},\dfrac{g}{2}\]

Answer 1

Hint: Using free body diagrams of blocks, the number of forces acting can be determined before and after cutting the string. Thus, equating the forces, the expression of acceleration can be obtained.

Complete step-by-step answer:
Consider the FBD of the blocks A and B.

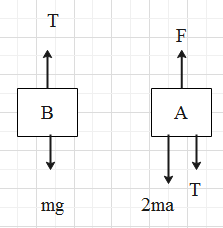
On block B, a normal force mg will be acting in the downward direction.  A tension T will also be acting on block B, but, in the upward direction. 
On block A, a normal force, that is, a net normal force 2mg will be acting in the downward direction. (One mg of block A and the other mg of block B), as the block B is connected next to block A. In this case, the tension T acts in the downward direction. Even a spring force F will also be acting on the block A, as the block is connected directly to the spring.
Consider the two blocks A and B to be a system.
The FBD of two blocks A and B to be a system

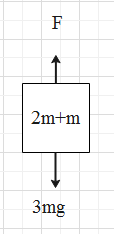
From the above FBD, we get a single force F acting in an upward direction and the normal force 3mg (2mg + mg) acting in the downward direction. So, we get, 
\[F=3mg\]
After instant cutting of the string tied between the blocks A and B. The forces acting on the blocks are as discussed below. 
Consider the FBD of the blocks A and B after cutting the string.

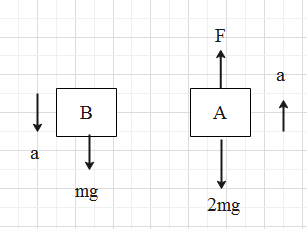
On block A, a force F acts in an upward direction and normal force 2mg acts in a downward direction. As the string is cut, there will be no tension acting on the block. The acceleration will be acting in an upward direction. 
So, the equations are,
\[F-2mg=2ma\]
As we have obtained the value of F, so we will substitute the same here.
\[\begin{align}
  & 3mg-2mg=2ma \\
 & \Rightarrow mg=2ma \\
 & \Rightarrow a={}^{g}/{}_{2} \\
\end{align}\]
Similarly, in the case of block B. The normal force mg will be acting in the downward direction and the acceleration a will be acting in the upward direction. As the string is cut, there will be no tension acting on the block. 
Thus, the equations are, 
\[\begin{align}
  & mg=ma \\
 & \Rightarrow a=g \\
\end{align}\]
Therefore, the acceleration of block A is \[{}^{g}/{}_{2}\] and that of block B is \[g\],
So, the correct answer is “Option B”.

Note: The direction of forces acting on the blocks should be taken care of. As, one wrong direction, will change the final result. Instead of the acceleration of blocks, the velocity can be asked by giving the value of time taken. In such a case, multiply the acceleration obtained by time.