Question

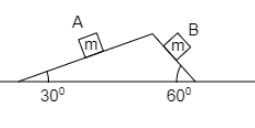
Two blocks $A$ and $B$ each of equal masses $m$ are released from the top of a smooth fixed wedge as shown in the figure. Find the magnitude of the acceleration of the centre of mass of the two blocks.

Answer 1

Hint: The acceleration of the centre of the mass is determined by using the vector equation of the acceleration of the two masses. The vector equation of the block$A$ and the vector equation of the block $B$ is used to find the magnitude of the acceleration of the centre of mass.

Complete step by step answer:
Given that, the block $A$ and the block $B$, both are having the same mass $m$,the block $A$ is sliding in the inclination of the surface of ${30^ \circ }$ and the block $B$ is sliding in the inclination of the surface of ${60^ \circ }$.Now, the force can be defined as the product of the mass of the object and the acceleration of the object.Let consider the inclination with respect to the x axis. So, the acceleration of the two mass in the vector form is,
The acceleration vector equation of the block $A$ is,
${\vec a_A} = mg\sin {30^ \circ }\hat i$
The acceleration vector equation of the block $B$ is,
${\vec a_B} = mg\sin {60^ \circ }\hat j$
Now, the acceleration of the centre of the mass of the two blocks can be written as,
${\vec a_{cm}} = \dfrac{{mg\sin {{30}^ \circ }\hat i + mg\sin {{60}^ \circ }\hat j}}{{{m_A} + {m_B}}}$
Here the mass of the two blocks are same, then

${\vec a_{cm}} = \dfrac{{mg\sin {{30}^ \circ }\hat i + mg\sin {{60}^ \circ }\hat j}}{{2m}}$
From the trigonometry, the values of $\sin {30^ \circ } = \dfrac{1}{2}$ and the $\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}$, then the above equation is written as,
${\vec a_{cm}} = \dfrac{{mg\left( {\dfrac{1}{2}} \right)\hat i + mg\left( {\dfrac{{\sqrt 3 }}{2}} \right)\hat j}}{{2m}}$
By taking the common terms from the above equation, then
${\vec a_{cm}} = \dfrac{{mg}}{{4m}}\left( {\hat i + \sqrt 3 \hat j} \right)$
By cancelling the terms in the above equation, then
${\vec a_{cm}} = \dfrac{g}{4}\left( {\hat i + \sqrt 3 \hat j} \right)$

By changing the vector equation to the magnitude, then
${a_{cm}} = \dfrac{g}{4}\sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} $
On further simplification in the above equation, then
${a_{cm}} = \dfrac{g}{4}\sqrt 4 $
By taking the square root in the above equation, then
${a_{cm}} = \dfrac{g}{4} \times 2$
On dividing the terms in the above equation, then
$\therefore{a_{cm}} = \dfrac{g}{2}$
Thus, the above equation shows the centre of the mass.

Note: When the two blocks are sliding in the inclined plane, then the acceleration of the centre of the mass of the two blocks is determined by using the trigonometric function. While using the trigonometric function, the students will give more concentration in the first step which shows the acceleration of the centre of the mass.